Как определяется предельная норма замещения набора из двух товаров? Постановка задачи об оптимальном наборе товара с данным уровнем полезности (с данной стоимостью) и ее решение.
Ответ: Предельной нормой замещения товара XK товаром XL называется отношение предельных полезностей товаров XK и XL:
MRSXK,XL(M)=U’Xk(M)/U’XL(M)= -∆XL /∆XK
В числителе этой формулы находится предельная полезность того товара, который замещают, а в знаменателе – товара, на который заменяют
Предельная норма приблизительно равна количеству товара XL, которое может заменить единицу товара XK так, чтобы полезность набора товаров не изменилась:
MRSXK,XL(M) = -∆XL/∆XK
Знак «минус» в этой формуле ставится для того, чтобы предельная норма замещения была неотрицательной.
Задача об оптимальном наборе
1.Выбор самого дешевого набора товаров с данным уровнем полезности.
Если набор товаров (x1,x2) оптимален среди остальных и функция полезности U(x1,x2)=U0, то MRSX1,X2(M)=р1/р2
2. Самый полезный набор товаров с данной стоимостью.
U (x1,x2)=c1
U (y1,y2)=c2
Если с2>с1, то набор (y1,y2) более полезен, чем (x1,x2)
Как определяется предельная норма замещения набора из двух ресурсов? Постановка задачи об оптимальном производственном плане с данным уровнем издержек (с данным объемом производства) и ее решение.
Ответ: Предельной нормой замещения ресурса XK ресурсом XL называется отношение предельных полезностей ресурсов XK и XL:
MRSXK,XL(M)=U’XK(M)/U’XL(M)= -∆XL /∆XK
В числителе этой формулы находится предельная полезность того ресурса, который замещают, а в знаменателе – ресурса, на который заменяют
Предельная норма приблизительно равна количеству ресурса XL, которое может заменить единицу ресурса XK так, чтобы полезность набора ресурсов не изменилась:
MRSXK,XL(M) = -∆XL/∆XK
Знак «минус» в этой формуле ставится для того, чтобы предельная норма замещения была неотрицательной.
1.Задача о достижении максимального уровня производства при заданном уровне издержек.
q1p1+q2p2=c1 – уравнение изокосты, показывающей наибольший объем производства при заданном уровне издержек.
2. Минимизация издержек при данном объеме производства:
с(q1q2)-q1p1+q2p2 – функция издержек
q1,q2 – объем ресурсов
p1,p2 – стоимость ресурсов
Q(q1,q2)=c2 – уравнение изокванты, показывает другие планы с тем же объемом производства, но требующие больших издержек.
М (q1,q2) ,будет оптимален, если MRSq1,q2=Q’q1(M)/Q’q2(M)=р1/р2
Постановка взаимно-двойственных задач. Поясните (можно на примере) экономическую суть понятия двойственности.
Ответ: Пусть имеется некоторая задача линейного программирования вида
.
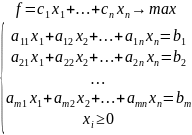Двойственной задачей к данной называется
задача вида
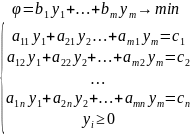
Экономическая сущность состоит в том, что предприятие может перейти от решения задачи максимизации прибыли к задаче минимизации издержек производства.