1. Задача оптимизации. Постановка задач математического и линейного программирования. Примеры задач оптимизации с экономическим содержанием.

Ответ: Рассмотрим некоторое множество X, на котором задана функция f(x). Задачей оптимизации называется задача нахождения наибольшего или наименьшего значения функции f(x), x∈X. Задачей математического программирования называется задача максимизации [минимизации] функции f(x), x∈X при выполнении системы неравенств . Если функции f(x), g₁(x),…, g_n(x) – линейные функции, то задача f(x)opt называется задачей линейного программирования. Примерами задач оптимизации могут являться производственная функция, функция полезности и т.д.

2. Производственная функция. Однофакторные и многофакторные производственные функции. Примеры производственных функций.

Ответ: Производственная функция – зависимость результата производственной деятельности от обусловивших его факторов. Например, Q=Q(x₁,…,x_n) – объем продукции, изготовленной при использовании ресурсов X₁,…,X_n в объемах x₁,…,x_n. Если n=1, то моель называется многофакторной, если n>1 – многофакторной. Примеры производственных функций: функция Кобба-Дугласа, CES-производственная функция, производственная функция Леонтьева

3. Виды производственных функций. Изокванты. Приведите пример производственной функции и ее изоквант.

Ответ: 1) Линейная: Q(x₁,…,x_n)= =a₀+a₁x₁+…+a_nx_n.

2) Мультипликативная: Q= a₀*x₁^a1*…*x_n^an. a_i>0, i=1,…,n

3) CES-производственная функция: имеет вид Q(K,L)=(C₁*K^-ρ+C₂*L^-ρ)^-p/ρ, где C₁,C­₂>0, ρ<1. В этой модели замещение одного ресурса другим невозможно.

Изоквантой называется линия уровня двухфакторной производственной функции.

4. Функции полезности. Линии безразличия. Приведите пример функции полезности и укажите ее линии безразличия. Поясните, как найти оптимальный набор товаров при заданном бюджетном множестве.

Ответ: Функция полезности – зависимость результата некоторого действия от уровня (интенсивности) этого действия. Функцией полезности называется функция, определенная на множестве возможных наборов товаров и принимающая наибольшее значение на том из двух наборов, который предпочтительнее потребителю. Линии уровня функции полезности называются линиями безразличия.

Пусть I – денежная сумма, которую потребитель может потратить на приобретение товаров X₁,…,X_n по ценам p₁,…,p_n, тогда x₁p₁+…+x_np_n≤I – бюджетное ограничение. Множество наборов товаров, удовлетворяющих бюджетным ограничениям, называется бюджетным множеством. Оптимальный набор товаров при заданном бюджетном множестве находится как набор товаров, при котором соответствующая функция полезности принимает максимальное значение.

5. Функция спроса и его эластичность. Как связаны эластичность спроса и эластичность выручки? Ответ обоснуйте.

Ответ: Функция спроса – зависимость объема спроса на товары или услуги от цены D=D(p). Эластичностью спроса называется величина, показывающее относительное изменение объема спроса под влиянием изменения цены, которая находится по формуле 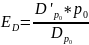. При неэластичном спросе изменение выручки прямо пропорционально изменению цен, при эластичном спросе – обратно, при единичном – не меняется.