14. Закон распределения дискретной случайно величины. Многоугольник распределения.

Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретной случайной величины.

            Закон распределения может быть задан аналитически, в виде таблицы или графически.

            Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения.

Законом распределения случайной дискретной величины (X) называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины (x1,x2,...xn) и соответствующими им вероятностями (p1,p2,... ,pn). При этом события (x1,x2,...xn) образуют полную группу (т.е. появление одного из них является достоверным событием), что означает

                                                                                     (1)

Про случайную величину X в таком случае говорят, что она подчинена данному закону распределения.

Простейшей формой задания этого закона является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности:

Возможное значение X	X1	Х2	...	Хn
Вероятность	Р1	Р2	...	Рn

Такая таблица называется таблицей распределения (вероятностей) случайной величины X.

Графически закон распределения дискретной случайной величины можно представить в виде многоугольника распределения – ломаной, соединяющей точки плоскости с координатами (xi, pi).

x1 x2 x3 x4 x5

            Графическое представление этой таблицы называется многоугольником распределения.  При этом сумма все ординат многоугольника распределения представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.

15. Функция распределения и её свойства. Вероятность попадания случайной величины на заданный интервал.

Функцией распределения F(x) случайной величины Х называется вероятность того, что случайная величина примет значение, меньшее х:

F (x) = p (X < x). (4.1)

Свойства функции распределения.

0 ≤ F(x) ≤ 1.

Действительно, так как функция распределения представляет собой вероятность, она может принимать только те значения, которые принимает вероятность.

Функция распределения является неубывающей функцией, то есть F(x2) ≥ F(x1) при х2 > x1. Это следует из того, что F(x2) = p(X < x2) = p(X < x1) + p(x1 ≤ X < x2) ≥ F(x1).

В частности, если все возможные значения Х лежат на интервале [a, b], то F(x) = 0 при х ≤ а и F(x) = 1 при х ≥ b. Действительно, X < a – событие невозможное, а X < b – достоверное.

Вероятность того, что случайная величина примет значение из интервала [a, b], равна разности значений функции распределения на концах интервала:

p ( a < X < b ) = F(b) – F(a).

Если R — это непрерывная случайная величина, которая распределена равномерно в интервале (0, 1), а r — ее возможные значения, то вероятность попадания величины R (в результате испытания) в интервал (с, d), принадлежащий интервалу (0, 1), равна его длине: В самом деле, плотность рассматриваемого равномерного распределения равна:

а значит, вероятность попадания случайной величины R в интервал (с, d) будет:

17. Математическое ожидание случайной величины и его свойства.

20. Математическое ожидание и дисперсия числа появления события в независимых опытах.

Математическое ожидание числа появления события в схеме независимых испытаний. Пусть производится n независимых опытов, вероятность появления события в каждом из которых равна Р. Число появлений события в этих n опытах является случайной величиною Х распределённой по биномиальному закону. Однако, непосредственное вычисление её среднего значения громоздко. Для упрощения воспользуемся разложением, которым будем пользоваться в дальнейшем неоднократно:  Число   появления события в n опытах состоит из числа появлений события в отдельных опытах, т.е.

где   имеет закон распределения (принимает значение 1, если событие в данном опыте произошло, и значение 0, если событие в данном опыте не появилось).

	0	1
Р	1-р	р

Поэтому

или

т.е. среднее число появлений события в n независимых опытах равно произведению числа опытов на вероятность 5

Дисперсия числа появления события в схеме независимых испытаний.

 Производится n независимых испытаний и вероятность появления события в каждом испытании равна р. Выразим, как и прежде, число появления события Х через число появления события в отдельных опытах

Так как опыты независимы, то и связанные с опытами случайные величины   независимы. А в силу независимости   имеем

	0	1
Р	1-р	р

Но каждая из случайных величин имеет закон распределения и  , поэтому по определению дисперсии

,

где q=1-p

В итоге имеем  , 

Среднее квадратическое отклонение числа появления событий в n независимых опытах равно  .

22. Закон равномерного распределения.

Равномерный закон распределения.

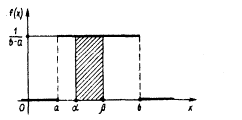
Определение. Непрерывная случайная величина Х имеет равномерное распределение на отрезке [а, в], если на этом отрезке плотность распределения вероятности случайной величины постоянна, т. е. если дифференциальная функция распределения f(х)имеет следующий вид:

Иногда это распределение называют законом равномерной плотности. Про величину, которая имеет равномерное распределение на некотором отрезке, будем говорить, что она распределена равномерно на этом отрезке.

Найдем значение постоянной с. Так как площадь, ограниченная кривой распределения и осью Ох, равна 1, то

откуда с=1/(b-a).

 Теперь функцию f(x) можно представить в виде

  

Построим функцию распределения F(x), для чего найдем выражение F(x) на интервале [a, b]:

: Графики функций f(x) и F(x) имеют вид:

 Найдем числовые характеристики.

Используя формулу для вычисления математического ожидания НСВ, имеем:

22.

Таким образом, математическое ожидание случайной вели чины, равномерно распределенной на отрезке [a, b] совпадает с серединой этого отрезка.

Найдем дисперсию равномерно распределенной случайной величины

откуда сразу же следует, что среднее квадратическое отклонение:

Найдем теперь вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал (,), принадлежащий целиком отрезку

[a, b]: 

Геометрически эта вероятность представляет  собой  площадь заштрихованного прямоугольника. Числа а и b называются параметрами распределения и однозначно определяют равномерное распределение.

23. Экспонентный закон распределения.