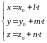15. Уравнение плоскости в r3 через 3 точки(д);2 вида общего уравнения плоскости в r3(2 доказательства).(каноническое и параметрическое).

Даны три точки

,

не лежащие на одной прямой. Требуется написать уравнение плоскости, проходящей через эти три точки. Из геометрии известно, что такая плоскость существует и единственная. Так как она проходит через точку  , то ее уравнение имеет вид

,      (9)

где  ,  ,   одновременно не равны нулю. Так как она проходит еще через точки  ,  , то должны выполняться условия:

                                          (10)

Составим однородную линейную систему уравнений относительно  неизвестных  ,  ,  :

                                           (11)

Здесь   есть произвольная точка, удовлетворяющая уравнению плоскости (9). В силу (9) и (10) системе (11) удовлетворяет нетривиальный вектор  , поэтому определитель этой системы равен нулю

.

Мы получили уравнение вида (9), т. е. уравнение плоскости, в чем легко убедиться, разложив полученный определитель по элементам первой строки. При этом эта плоскость проходит через точки  ,  ,  , что вытекает из свойств определителя. Наша задача решена.

Уравнение (12) можно еще написать и в следующем виде:

.                         (13)

Если из первой, третьей и четвертой строк определителя в (13) вычесть вторую строку, то он не изменится. Разлагая результат по элементам четвертого столбца, получим уравнение (12).

Праметрическое

Аналитическое

16. Нормальное уравнение плоскости и расстояние от точки до плоскости (вывод уравнения, д).

Нормальным уравнением плоскости называется её уравнение, написанное в виде

x cos α + y cos β + z cos — p = 0, (1)

где cos α, cos β, cos  суть направляющие косинусы нормали плоскости, р — расстояние до плоскости от начала координат. При вычислении направляю­щих косинусов нормали следует считать, что она направлена от начала ко­ординат к плоскости (если же плоскость проходит через начало координат, то выбор положительного направления нормали безразличен).

Пусть М* — какая угодно точка пространства, d — расстояние от неё до данной плоскости. Отклонением о точки М* от данной плоскости называется число + d, если точка М* и начало координат лежат по разные стороны от данной плоскости, и число — d, если они лежат по одну сторону от данной плоскости (если М* лежит на самой плоскости, то отклонение равно нулю).

Если точка М* имеет координаты x*, у*, z*, а плоскость задана нор­мальным уравнением

x cos α + y cos β + z cos — p = 0, то отклонение точки М* от этой плоскости даётся формулой

δ = x*cos α + y* cos β + z* cos — p

Очевидно, d= | δ |.

Общее уравнение плоскости

Ах + By + Cz + D = 0

приводится к нормальному виду (1) умножением на нормирующий множи­тель, определяемый формулой

;

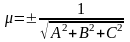знак нормирующего множителя берётся противоположным знаку свободного члена нормируемого уравнения.

17. Взаимное расположения двух плоскостей: α₁ перпендикулярно α₂, α₁ II α₂ (2д).

 Возможны два случая взаимного расположения двух плоскостей в пространстве:

• Параллельны

• Пересекаться

Опр. Две плоскости в пространстве называются параллельными, если они не пересекаются, в  противном случаи они пересекаются.

Теорема1: Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Доказательство:

Пусть  и - данные плоскости, а1 и а2 - прямые в плоскости , пересекающиеся в точке А, в1 и в2 - соответственно параллельные им прямые в

плоскости . Допустим, что плоскости  и  не параллельны, т.е. пересекаются по некоторой прямой с. По теореме прямые а1 и а2, как параллельные прямым в1и в2, параллельны плоскости , и поэтому они не

пересекают лежащую в этой плоскости прямую с. Таким образом, в плоскости  через точку А проходят две прямые (а1 и а2) , параллельные прямой с. Но это невозможно по аксиоме параллельных. Мы пришли к противоречию ЧТД.

Перпендикулярные плоскости: Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.

Теорема2: Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Доказательство:

Пусть  - плоскость, в -перпендикулярная ей прямая,  - плоскость, проходящая через прямую в, с - прямая, по которой пересекаются плоскости  и . Докажем, что плоскости  и  перпендикулярны. Проведем в плоскости  через точку пересечения прямой в с плоскостью  прямую а,

перпендикулярную прямой с. Проведем через прямые а и в плоскость . Она перпендикулярна прямой с, т.к. прямая с перпендикулярна прямым а и в. Т. к. прямые а и в перпендикулярны, то плоскости  и  перпендикулярны. ч.т.д.

18. Каноническое и параметрическое уравнение прямой в R^3. Уравнение через 2 точки в R^3 и уравнение плоскости в отрезках (рисунки, уравнения, самостоятельно конспект).

Канонические и параметрические уравнения прямой

Поставим следующую задачу:

Составить уравнения прямой, проходящей через данную точку M(x₀, y₀, z₀) параллельно данному вектору 

  = {l, m, n} ≠ 

 (вектор  называется направляющим вектором прямой).

Решение. Пусть N(x, y, z) — произвольная точка пространства. Построим вектор MN = {x − x₀,  y − y₀,  z − z₀} (рис.1).

Очевидно, что точка N принадлежит прямой тогда и только тогда, когда вектор MN коллинеарен вектору 

 = {l,  m,  n} , т.е. когда их координаты пропорциональны:

(1)

Эти уравнения называются каноническими уравнениями прямой в пространстве.

Замечания.

1. От канонических уравнений легко перейти к общим уравнениям прямой, например:

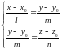
2. Одна или две координаты направляющего вектора прямой  могут быть равны нулю, это означает, что числитель соответствующей дроби тоже равен нулю.

Если в (1) ввести параметр t

то уравнения прямой можно записать в виде

Эти уравнения называются параметрическими уравнениями прямой. Они имеют механический смысл: если параметр t рассматривать как время, а x,  y,  z — как координаты материальной точки, то параметрические уравнения описывают равномерное прямолинейное движение точки со скоростью 

 = {l,  m,  n} ,   (x₀, y₀, z₀) —начальное положение точки (при t = 0 ).