Каноническое уравнение гиперболы в декартовой системе координат (вывод)

ОПРЕДЕЛЕНИЕ. Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от которых до двух фиксированных точек плоскости и есть величина постоянная и равная ( ).

Точки и называют фокусами гиперболы.

Получим уравнение гиперболы. Выберем декартову прямоугольную систему координат так, чтобы фокусы и лежали на оси на одинаковом расстоянии от начала координат. В такой системе координат точки и будут иметь координаты:

и ,

где . Пусть – текущая точка гиперболы. По определению гиперболы

,

⇒ ,

⇒ ,

Избавимся от квадратных корней:

,

⇒ ,

⇒ .

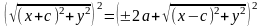Приведя подобные слагаемые, получим:

.

Снова возведем обе части в квадрат и приведем подобные слагаемые:

,

⇒ ,

⇒ ,

⇒ .

Так как по определению , то . Следовательно, , для некоторого числа , и последнее равенство примет вид: .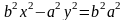

Разделим обе части этого равенства на и окончательно получим:

. (59)

Уравнение (59) называется каноническим уравнением гиперболы. Система координат, в которой гипербола имеет такое уравнение, называется ее канонической системой координат.

Каноническое уравнение параболы в декартовой системе координат (с выводом)

Пусть – некоторая прямая на плоскости, – некоторая точка плоскости, не лежащая на прямой .

ОПРЕДЕЛЕНИЕ. Параболой называется геометрическое место точек плоскости, расстояние от которых до фиксированной прямой и до фиксированной точки (не лежащей на прямой ) одинаково.

Точку называют фокусом параболы, прямую – директрисой.

Получим уравнение параболы. Пусть – расстояние от до . Выберем декартову прямоугольную систему координат так, чтобы директриса параболы была перпендикулярна оси , фокус лежал на положительной части и расстояние от начала координат до фокуса и до директрисы было одинаковым. В такой системе координат

и : .

Пусть – текущая точка параболы. По определению пара.

,

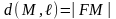т.е. , ⇒ .

Избавимся от квадратного корня: ,

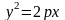⇒ (61)

Уравнение (61) называется каноническим уравнением параболы. Система координат, в которой парабола имеет такое уравнение, называется ее канонической системой координат.

Критерий подпространства

Пусть α – линейное пространство над F, α₁ – непустое подмножество в α. α₁ является подпространством линейного пространства α  , когда для любых элементов a,b ϵ α₁ и любого α ϵ F выполняются условия :

1. a-b ϵ α_1;

2. α*a ϵ α_1;

Док-во:

Необходимость:

α₁ – подпространство линейного пространства α => L₁ – линейное пространство =>

1. a-b = a+ (-b) ϵ L₁

2. α_*a ϵ L₁

a,b ϵ L₁ ,(-b) ϵ L₁

Достаточность:

1),2) => L₁ – линейное подпространство

По определению, a+b = b+a , (a+b)+c = a+ (b+c).

При любом a:

а-а = 0 ϵ L₁ ; (-1)*a = -a –противоположный элемент, -a ϵ L₁

(αβ) a = α (βa) ϵ L₁

(α+β)a = αa+βa

α(a+b) = αa+αb

1a = a

• L₁ – линейное пространство относительно операций определенных на L => L₁ ≤ L