Основные свойства определителя (одно из них доказать)

Свойства определителя:

1. При транспонировании матрицы ее определитель не меняется.

Док-во:

Посчитаем каждый определитель:

1. 

2. 

Делаем вывод что оба определителя у нас равны (ч.т.д)

2) При перестановке любых двух строк (столбцов) определитель меняет знак.

3) Общий множитель элементов любой строки (столбца) можно выносить за знак определителя.

4) Если все элементы k-й строки определителя |A| являются суммами двух элементов, то определитель равен сумме двух определителей |A₁| и |A₂|, у которых все строки кроме k-й совпадают со строками определителя |A|, а k-я строка в определителе |A₁| состоит из первых слагаемых, а в определителе |A₂| – из вторых слагаемых.

5) Определитель равен нулю если:

а) он имеет строку (столбец), состоящую из нулей;

б) он имеет хотя бы две одинаковые строки (столбца);

в) он имеет хотя бы две пропорциональные (т.е. отличающиеся множителем) строки (столбца);

г) хотя бы одна строка (столбец) является линейной комбинацией нескольких других строк (столбцов).

6) Критерий равенства нулю определителя.

Определитель равен нулю  хотя бы одна строка (столбец) является линейной комбинацией нескольких других строк (столбцов).

7) Определитель не изменится, если к каждому элементу i-й строки (столбца) прибавить соответствующий элемент k-й строки (столбца), умноженный на число α  0.

8) Если A и B – квадратные матрицы порядка n , то существует AB и BA, причем |AB|=|BA|=|A|·|B|.

Критерий равенства нулю определителя квадратной матрицы (с доказательством).

Определитель матрицы А равен нулю  его строки (столбцы) линейно зависимы.

ДОКАЗАТЕЛЬСТВО

1) Необходимость. Пусть . Тогда по определению базисного минора имеем  n.

Пусть , , , – строки матрицы А. Будем считать, что базисными строками являются строки , , , . Тогда по теореме о базисном миноре

.

Следовательно,

.

Так как коэффициент при не равен нулю, то строки матрицы А , , , линейно зависимы.

2) Достаточность. Пусть строки матрицы А линейно зависимы. Тогда по лемме о линейной зависимости, некоторая строка является линейной комбинацией остальных. По свойству определителей следует, что .

Свойства обратной матрицы (с доказательством).

Свойства обратной матрицы: 1) Если матрица А имеет обратную, то А и А^-1 – квадратные матрицы одного порядка.

Док-во:

Исходя из определения произведения матриц умножение матриц возможно тогда и только тогда, когда число столбцов матриц А равно числу строк матрицы А^-1. Следовательно, чтобы сущ-ли произведения А*А^-1 и А^-1*А необходимо, чтобы А и А^-1 имели соответственно размеры (n*m) и (m*n). Тогда матрица А^-1*А будет иметь размер (m*m). но бля равенства А*А^-1=А^-1*А=Е необходимо, чтобы размеры матриц А*А^-1 и А^-1*А совпадали, т.е. n=m (ч.т.д.)

2) Если обратная матрица сущ-ет, то она единственная

Док-во:

Предположим, что сущ-ет две матрицы В и С обладающие свойством А*В=В*А=Е и А*С=С*А=Е

Рассмотрим произведение В*А*С, которое сущ-ет в силу того, что матрицы А,В,С – квадратные матрицы одного порядка.

Тогда с другой стороны

В*А*С=(В*А)*С=Е*С=С

В*А*С=В*(А*С)=В*Е=В

Следовательно С=В

3)Если матрица А имеет обратную, то определитель матрицы А отличен от нуля.

Док-во:

По определению обратной матрицы имеет место равенство А*А^-1=Е, где Е – единичная матрица, определитель которой равен 1.

Для квадратных матриц А и В порядка n имеет место равенство |А*В|=|В*А|=|А|*|В|

Тогда |А*А^-1|=|А|*|А^-1|=|Е|=1!=0;

Следовательно, |А|!=0 и |А^-1|!=0

критерий существования обратной матрицы

Пусть – квадратная матрица порядка . Матрица имеет обратную тогда и только тогда, когда ее определитель отличен от нуля. Причем обратная матрица может быть найдена по формуле:

,

где – матрица из алгебраических дополнений элементов матрицы , т.е.

.

Матрица называется союзной для матрицы .

ДОКАЗАТЕЛЬСТВО

Необходимость утверждения доказана ранее (см. свойство 3 матриц, имеющих обратную). Требуется доказать только достаточность.

Пусть матрица – невырожденная. Тогда существует матрица . Докажем, что она является обратной к . Имеем

.

При имеем

,

и т.д.

.

Здесь использовали, что (следствие 1 теоремы Лапласа).

При

,

и т.д.

Здесь использовали (следствие 2 теоремы Лапласа).

Аналогично доказывается, что

.

Следовательно, . ∎

Матричный метод.

ОПРЕДЕЛЕНИЕ. Обратной к матрице A называется матрица, обозначаемая A^-1, такая, что A·A^-1=A^-1 · A=E.

СВОЙСТВА ОБРАТНОЙ МАТРИЦЫ

1) Если матрица A имеет обратную, то A и A^-1 – квадратные одного порядка.

2) Если обратная матрица существует, то она единственная.

3) Если матрица A имеет обратную, то определитель матрицы A отличен от нуля.

Квадратная матрица, определитель которой отличен от нуля, называется невырожденной.

Теорема. Пусть А – квадратная матрица порядка n.Матрица А имеет обратную тогда и только тогда, когда ее определитель |A| отличен от нуля. Причем обратная матрица А^-1 модет быть найдена по формуле: А^-1 = 1/|A| * S^T.

Где S – матрица, составленная из алгебраических дополнений элементов матрицы А, т.е. имеет вид S

Матрица S^T называется союзной (или присоеденительной) для матрицы А.

Док-во. Необходимость. Пусть квадратная матрица А порядка n имеет обратную матрицу. Докажем, что тогда её определитель |A| отличен от нуля (см. свойство 3 обратной матрицы)

Свойство 3. Если матрица А имеет обратную, то определитель матрицы отличен от нуля.

Док-во: По определению обратной матрицы имеет место равенство А * А^-1 = Е, где Е еденичная матрица определитель которой равен 1

Для квадратных матриц А и В порядка n имеет место равенство |A * B| = |B * A|, Тогда

|A * A^-1| = |A| * |A^-1| = |E| = 1 ≠ 0, => |A| ≠ 0 и |A^-1| ≠ 0.

Достаточность. Пусть матрица А – невырожденная, т.е. её определитель отличен от нуля. Тогда существует матрица 1/|A| * S^T , где S – матрица, составленная из алгебраических дополнений элементов определителя матрицы А, т.е. имеет вид

S

Докажем, что она является обратной к матрице А. Покажем, что при умножении матрицы А на матрицу А^-1 = 1 / |A| * S^T получим единичную матрицу порядка n.

Тогда A * A^-1 = A (1/|A| * S^T ) = 1 / |A| * (A * S^T) = в ходе преобразований =

Аналогично доказывается, что А^-1 * А = (1 / |A| * S^T ) * A = 1 / |A| * (S^T * A) = E

Следовательно, если |A| ≠ 0, то существует обратная матрица А^-1, которую можно найти по формуле A^-1 = 1 / |A| * S^T . Теорема доказана

Метод Крамера (формулировка теоремы с доказательством).

Если в системе линейных уравнений число уравнений и число неизвестных совпадает и , то система совместна и имеет единственное решение, которое может быть найдено по формулам

( ), (1)

где , а – определитель, получаемый из определителя заменой его -го столбца на столбец свободных членов.

Формулы (1) называются формулами Крамера.

ДОКАЗАТЕЛЬСТВО

Так как , то матрица имеет обратную и систему можно решить матричным методом, т.е.

⇒ .

Но выражение представляет собой разложение по -му столбцу определителя (см. следствие теоремы Лапласа 2, формулу 2

), где в -м столбце стоит столбец из свободных членов:

. Следовательно, .

Свойства решений СЛОУ (с доказательством).

Линейная комбинация конечного числа решений системы линейных однородных уравнений тоже является решением этой системы.

ДОКАЗАТЕЛЬСТВО: Запишем систему линейных однородных уравнений

(22)

в матричной форме: .

По условию и – решения системы. Следовательно, матрицы-столбцы

и

являются решениями матричного уравнения , т.е. и .

Рассмотрим линейную комбинацию матриц и с коэффициентами и . Так как

,

то матрица тоже является решением матричного уравнения . Значит, элементы матрицы будут решением системы уравнений (2). Но эти элементы и есть линейная комбинация решений и .

Деление отрезка в данном отношении (с выводом формул).

Говорят, что точка М₀ делит отрезок М₁М₂ в отношении если _.

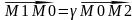Если , то точка М₀ лежит между точками М₁ и М_2. В этом случае говорят, что точка М₀ делит отрезок М₁М₂ во внутреннем отношении. Если то точка М₀ лежит на продолжении отрезка и говорят, что она делит его во внешнем отношении. Рассмотрим случай, когда :

_,

=> М₀

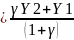X₀ Y₀ Z₀

Замечание, если точка М ₀ середина отрезка, то применяется та же самая формула, но в знаменателе стоит 2 (т.к. )

Теорема о сведении линейных операций над векторами к таким же операциям над их одноименными координатами (с доказательством).

Если вектор 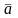имеет в базисе координаты {a₁, a₂, a₃}, вектор в этом же базисе {b₁, b₂, b₃}, то + в заданном базисе: {а₁+ b₁, а₂+ b₂, а₃+ b₃}

Если вектор имеет в базисе координаты {a₁, a₂, a₃}, то для любого действительного вектор = { a₁, a₂, a₃}

Доказательство раз:

= a₁ + a₂ + a_3, = b₁ + b₂ + b₃

+ = a₁ + a₂ + a₃ + b₁ + b₂ + b₃ = (а₁+ b₁) + (а₂+ b₂) + (а₃+ b₃) => + = {а₁+ b₁, а₂+ b₂, а₃+ b₃}

Доказательство два:

= ( a₁ + a₂ + a₃) = a₁ + a₂ + a₃ => = { a₁, a₂, a₃}

Критерий линейной зависимости двух векторов.

Два свободных вектора линейно зависимы  они коллинеарные

Доказательство:

1) Необходимость. Пусть векторы и – линейно зависимы. Тогда по определению существуют числа (хотя бы одно из них отличное от нуля) такие, что выполняется равенство . Пусть, например, . Тогда . Следовательно,  .

2) Достаточность. Пусть  . Тогда такое, что выполняется равенство . Тогда . Так как и , то векторы и – линейно зависимы.

Критерий линейной зависимости трёх векторов

Три свободных вектора линейно зависимы  они компланарны.

Доказательство:

1) Необходимость. Пусть векторы , и – линейно зависимы. Тогда по определению существуют числа (хотя бы одно из них отличное от нуля) такие, что выполняется равенство . Пусть, например, .

Тогда . Следовательно, , и лежат в одной плоскости, т.е. они компланарны.

2) Достаточность. Пусть , и – компланарны.

Рассмотрим 2 случая.

а) Пусть  . Тогда такое, что выполняется равенство . Тогда . Следовательно, векторы , и – линейно зависимы.

б) Пусть и не параллельны. Тогда и образуют базис. Следовательно, вектор можно представить в виде линейной комбинации базисных векторов. Тогда векторы , и – линейно зависимы.

Скалярное произведение векторов: определение и свойства (доказать).

Скалярное произведение векторов

Скалярным произведением двух ненулевых векторов   и  называется число, равное произведению модулей этих векторов на косинус угла между ними, т.е. число

Если = 0 или = 0, то скалярное произведение векторов полагают равным нулю.

Свойства скалярного произведения векторов

1. Скалярное произведение векторов коммутативно, т.е. ( , ) = ( , ).

( , ) = | |∙ | |∙ cos( ), а ( , ) = | |∙| |∙ cos( ). И так как

| |∙ | |= | |∙| |, как произведение чисел и cos( ) = cos( ), то

( , ) = ( , ).

2. Скалярное произведение ненулевых векторов  и равно произведению длины вектора на проекцию вектора на вектор (длины вектора на проекцию на ). Так как

то получаем: .

3. Числовой множитель любого из 2-х векторов можно вынести за знак скалярного произведения: (λ , ) = ( , λ ) = λ( , ).

4. Е сли один из векторов записан в виде суммы, то их скалярное произведение тоже можно записать в виде суммы.

5. Скалярное произведение вектора на себя (скалярный квадрат вектора) равно квадрату его длины. Т.е. ( ) = | |².

( ) = | |∙| | cos0 = | |∙| | = | |².

| | = ).