7. Определить выражения для комплексного вектора Пойнтинга для двух случаев:

а). f>f_кр

б). f<f_кр

Определить среднее за период значение плотности потока энергии и амплитуду плотности реактивного потока энергии.

Общая формула для расчета вектора Пойнтинга имеет следующий вид при , ,

(15)

Где - это комплексная амплитуда напряженности электрического поля, а - это комплексно – сопряженная амплитуда напряженности магнитного поля.

а). f>f_кр

Используя формулы выражения (5) найдем проекции и комплексно-сопряженного вектора магнитного поля:

(16)

Подставляем проекции , и в формулу (15):

(17)

(18)

б). f<f_кр

Используя формулы выражения (9), найдем проекции и комплексно-сопряженного вектора магнитного поля:

(19)

Подставляем проекции , и в формулу (15):

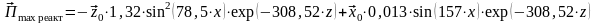
8. Вычислить средний за период поток энергии через поперечное сечение трубы.

Для этого проинтегрируем по площади поперечного сечения среднюю за период плотность потока энергии , определяемую выражением (17):

(20)

Где - это поперечное сечение волновода (рис.1), - элементарная площадка в этом поперечном сечении.

Конечное выражение для имеет вид:

(21)

Подставив в полученное выражение все необходимые значения констант и параметров для , найдём численное значение среднего за период потока энергии, проходящей через поперечное сечение трубы. Получим:

9. Определить фазовую скорость Vф и скорость распространения энергии Vэ рассматриваемой волны. Рассчитать и построить графики зависимостей Vф и Vэ от частоты.

Рассчитаем фазовую скорость волны с учетом , где -скорость света в среде.

На частоте f1 :

Для расчета скорость распространения энергии воспользуемся соотношением [1]:

Отсюда скорость распространения энергии равна:

На частоте f1 :

Запишем выражение, характеризующее зависимость фазовой скорости от частоты:

Указанные формулы были запрограммированы в математическом пакете MathCAD 15, где были построены графики зависимостей V_ф и V_э от частоты. Результаты показаны на Рис. 14.

_{Из построенного графика видно, что Vф на граничной частоте стремится к бесконечности, а при увеличении частоты приближается к скорости света в данной среде. Vэ на граничной частоте стремится к нулю и переноса энергии не происходит. При увеличении частоты Vэ приближается к скорости света в данной среде. Таким образом, использования волновода на граничной частоте и близко к ней невозможно.}

рис. 14

10. Считая, что стенки трубы выполнены из реального металла имеющего Сим/м, на основе граничных условий Леонтовича-Щукина определим коэффициент затухания для заданной волны.

Формула для расчета коэффициента затухания на основе граничных условий Леонтовича-Щукина имеет вид [1]:

(22)

(23)

_{L - контур поперечного сечения металлических элементов линии передачи (рис.1). Интеграл по этому контуру разбивается на четыре интеграла. По нижней стенке при y=0, касательными будут x-я и z-я составляющие (первый и второй интегралы). По верхней стенке при x=0, касательными будут z-я и y-я составляющие (третий и четвертый интегралы).}

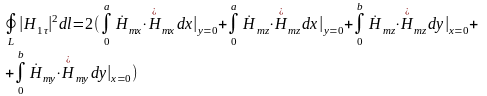(24)

_- средний за период поток энергии через поперечное сечение трубы, рассчитанный ранее по формуле (21).

_{Используя выражения (5) и (1}6) , найдем произведения

Аналогично найдем произведение и

Используя полученные произведения, вычислим интегралы, входящие в выражение (24):

Подставляем вычисленные интегралы в выражение (24):

(25)

Подставим в формулу (22) выражения (21), (23) и (25):

(26)