
- •Техническое задание.
- •Используя уравнения Максвелла, определить комплексные амплитуды составляющих вектора
- •Записать выражения для мгновенных значений всех составляющих векторов и для двух случаев:
- •Рассчитать и построить графики зависимостей амплитуд составляющих векторов поля.
- •Найти комплексные амплитуды плотностей поверхностных токов и зарядов на всех стенках трубы
- •Определить выражения для комплексного вектора Пойнтинга для двух случаев:
- •Определить фазовую скорость Vф и скорость распространения энергии Vэ рассматриваемой волны. Рассчитать и построить графики зависимостей Vф и Vэ от частоты.
- •Считая, что стенки трубы выполнены из реального металла имеющего Сим/м, на основе граничных условий Леонтовича-Щукина определим коэффициент затухания для заданной волны.
- •Рассчитаем и построим частотную зависимость коэффициента затухания волны в волноводе.
Федеральное агентство связи
Московский технический университет связи и информатики
Кафедра технической электродинамики и антенн
Анализ электромагнитного поля в прямоугольном волноводе
Проверил профессор кафедры ТЭДиА Выполнил студент группы ПС1001
Муравцов Александр Дмитриевич. Чопчиц Оксана
Факультет РиТ
Москва 2012
Содержание.
1. Техническое задание………………………………………………………………...............................................3
2.
Определение комплексных амплитуд
составляющих вектора
 и
и
 ……………………5
……………………5
3. Определение диапазона частот, в котором рассматриваемое поле – бегущая волна…………………………………………………………………..................................................................................7
4. Выражения для мгновенных значений всех составляющих векторов и …..……8
5. Расчет и построение графиков зависимостей амплитуд составляющих
векторов поля от координат x, y, z…………………………………………………...................................10
6. Проверка выполнения граничных условий………………………………………………………...….17
7. Определение комплексных амплитуд плотностей поверхностных токов и зарядов……………………………………………………..…………………………………………………………………18
8. Определение выражений для комплексного вектора Пойнтинга. Среднее за период значение плотности потока энергии. Амплитуда плотности реактивного потока энергии……………………………………………………………………………………………………………………….21
9. Вычисление среднего за период потока энергии через поперечное сечение трубы…………………………………………………………………………………………………………………………..23
10. Определение фазовой скорости и скорости распространения энергии.
Расчет и построение графиков их зависимостей от частоты…………………………………….24
11. Определение коэффициента затухания волны…………………………………………………….26
12. Расчёт и построение частотной зависимости коэффициента затухания
волны в волноводе……………………………………………………………………………………………………..29
13. Определение типа волны, распространяющейся в волноводе, структура силовых линий электрического и магнитного полей этой волны, структура силовых линий плотности поверхностного тока проводимости, протекающего по стенкам волновода…………………………………………………………………………………………………………………...31
14. Вывод…………………………………………………………………………………………………………………….34
15. Использованная литература…………………………………………………………………………………34
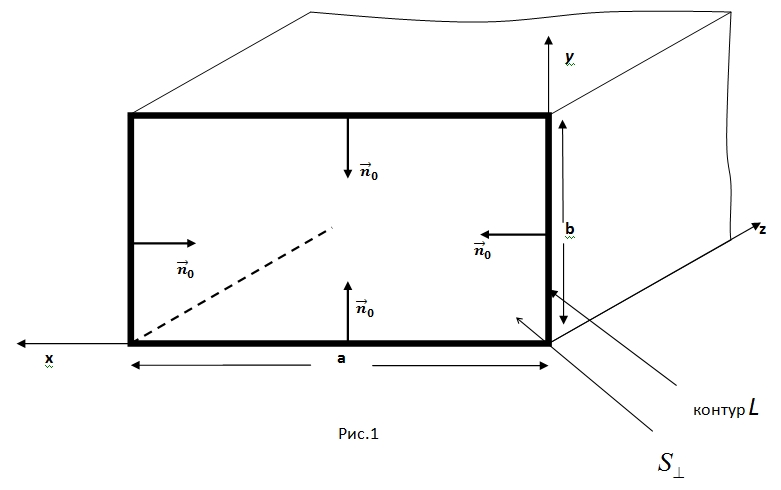
Техническое задание.
В
полой трубе прямоугольного сечения
(Рис.1) с идеально проводящими стенками
создано монохроматическое электромагнитное
поле. Труба заполнена однородной
изотропной средой без потерь, абсолютные
диэлектрическая и магнитная проницаемости
равны
 и
и
 соответственно.
Известно, что комплексная амплитуда
вектора
соответственно.
Известно, что комплексная амплитуда
вектора
 имеет
одну составляющую:
имеет
одну составляющую:
 где
где


 f
– частота электромагнитных колебаний;
f
– частота электромагнитных колебаний;
 -
длина волны, свободно распространяющейся
в однородной изотропной непроводящей
среде с параметрами
и
;
-
длина волны, свободно распространяющейся
в однородной изотропной непроводящей
среде с параметрами
и
;
 -
скорость света в этой среде.
-
скорость света в этой среде.
Исходные данные:
№ вар. |
Е0, В/м |
|
|
а, см |
b, см |
|
|
|
1 |
5,7 |
2 |
1 |
4 |
2 |
1,00 |
5,0 |
1,0 |
Используя уравнения Максвелла, определить комплексные амплитуды составляющих вектора
В
условии технического задания нам дана
комплексная амплитуда вектора :
:
 ,
с помощью которой находим выражения
для комплексных амплитуд составляющих
вектора
,
с помощью которой находим выражения
для комплексных амплитуд составляющих
вектора
Запишем
проекции комплексной амплитуды вектора
 на оси координат:
на оси координат:
 (1)
(1)
Электрическое
и магнитное поля связаны через уравнения
Максвелла. Воспользуемся вторым
уравнением Максвелла в комплексной
форме для определения комплексной
амплитуды вектора
 ,
откуда:
,
откуда:

Спроектируем на оси:



Разложим
 по
координатам:
по
координатам:

Тогда
составляющие комплексной амплитуды
вектора
 равны
соответственно:
равны
соответственно:
 (2)
(2)
 (3)
(3)
 (4)
(4)
Найдем выражения для частных производных составляющих комплексной амплитуды вектора по соответствующим координатам:






Подставляя найденные значения частных производных в (2), (3) и (4), получим итоговые выражения для комплексных амплитуд составляющих вектора


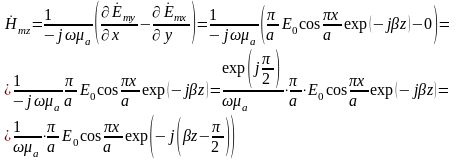
Комплексные
амплитуды составляющих вектора

 (5)
(5)
Определить диапазон частот, в котором параметр β-действительное число.
По
условию задачи ,
значит,
,
значит,
 будет
действительны в случае, если
будет
действительны в случае, если
 ,
т. е. при
,
т. е. при
 ,
,
 ,
,

Этому диапазону длин волн соответствует диапазон частот:
 ,
где
,
где


Таким образом, если частота волны не принадлежит рассчитанному диапазону частот, то является мнимой величиной. Для этого случая представим:
 ,
где
,
где

Записать выражения для мгновенных значений всех составляющих векторов и для двух случаев:
а). f>fкр
б). f<fкр
Для
получения выражений для мгновенных
значений составляющих векторов поля
необходимо домножить их комплексные
амплитуды на выражение
 и, выделить действительную часть.
и, выделить действительную часть.
а) f>fкр:
В этом случае выражения для комплексных амплитуд составляющих используются без изменений. Получим:

 (6)
(6)

 (7)
(7)

б). f<fкр:
В этом случае в выражениях (1) и (5) необходимо произвести замену, описанную в пункте 2.
 ,
получаем:
,
получаем:
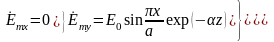 (8)
(8)
 (9)
(9)
Найдем мгновенные значения составляющих векторов и :

 (10)
(10)
 (11)
(11)

 (12)
(12)




 ,
ГГц
,
ГГц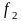 ,
ГГц
,
ГГц