§ Несобственные интегралы.

Интегралы с бесконечными пределами и интегралы от неограниченных функций называются несобственными интегралами.

Если существует конечный предел в правой части равенства, то несобственный интеграл называется сходящимся, в противном случае – расходящимся.

Аналогично определяются:

Пример. Исследовать на сходимость несобственный интеграл

Решение. По определению

Существование последнего предела зависит от величины L. Если то

интеграл сходится.

Если то интеграл расходится.

При = 1 интеграл также расходится, ибо

4.7. Дифференциальные уравнения.

Дифференциальным уравнением называется уравнение, связывающее независимую переменную х, искомую функцию и ее производные различных порядков.

Порядком дифференцированного уравнения называется порядок старшей производной, входящей в это уравнение.

§ Дифференциальные уравнения с разделяющимися переменными.

Дифференциальным уравнением с разделяющимися переменными называется уравнение вида где - функции только от х, - функции только от у.

Данное уравнение делим на произведение , т.е. приводим к уравнению с разделенными переменными:

Общий интеграл последнего уравнения:

Пример. Проинтегрировать уравнение . Найти интегральную кривую, проходящую через точку М (3; -4).

Решение. Данное уравнение можно переписать так:

Полученное уравнение является уравнением с разделенными переменными. Интегрируя, получим

Полагая (т.к. ).

Общий интеграл запишем в виде

Геометрически общий интеграл представляет собой семейство окружностей радиусов С с центром в начале координат.

Решим задачу Коши, т.е. Найдем ту окружность, которая проходит через точку М (3; -4). Подставляя координаты точки М в уравнение находим или Подставив значение в общий интеграл, получим искомую окружность

§ Однородные дифференциальные уравнения первого порядка.

Дифференциальное уравнение

называется однородным , если коэффициенты и являются однородными функциями одного и того же измерения n, т.е. функциями, для которых при любом k выполняются тождества.

Уравнение можно привести к виду с помощью подстановки где u-новая неизвестная функция, тогда однородное уравнение преобразуется в уравнение с разделяющимися переменными.

Пример. Проинтегрировать однородное дифференциальное уравнение

Решение. Коэффициенты при dy и dx соответственно равны:

Докажем, что функции и являются однородными функциями первой степени:

Положим y=ux, тогда dy=udx+xdu. Подставим эти выражения в исходное уравнение:

получим уравнения с разделяющимися переменными.

Разделяя переменные, проинтегрируем

откуда

откуда подставляя выражение находим

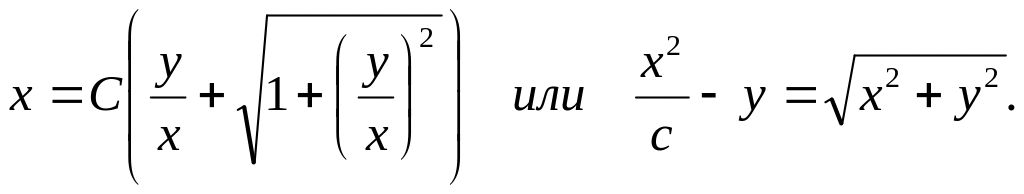
Возводя в квадрат обе части уравнения и сокращая на , получим общий интеграл , который геометрически представляет собой семейство парабол с вершинами на оси Оу.

§ Линейные дифференциальные уравнения первого порядка.

Уравнения вида называются линейными, первое – относительно у, , второе – относительно х, Если то уравнение называется линейным однородным; если

- линейным неоднородным.

Линейное однородное – это уравнение с разделяющимися переменными.

Неоднородное линейное уравнение может быть сведено к решению двух уравнений с разделяющимися переменными. Для этого используется подстановка тогда

В качестве v выбирают одну из функций, удовлетворяющих уравнению

тогда функция u определяется из уравнения .

Пример. Найти общее решение линейного дифференциального уравнения

Решение. Положим Уравнение перепишем в виде:

Выберем v так, чтобы выражение в скобках обратилось в нуль, тогда

Уравнение имеет вид при

. Следовательно

Или С – общее решение исходного уравнения.