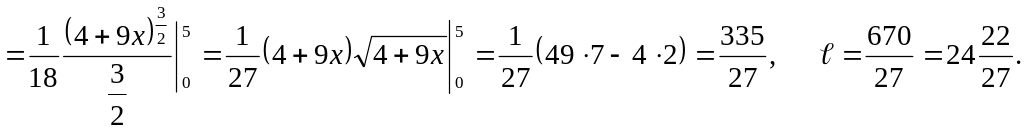Интегрирование рациональных функций
Интегрирование рациональных функций проводится по общему правилу интегрирования рациональных дробей:
если дробь неправильна, то необходимо представить ее в виде суммы многочлена и правильной дроби;
разложив знаменатель правильной рациональной дроби на множители, представить ее в виде суммы простейших рациональных дробей;
проинтегрировать многочлен и полученную сумму простейших дробей.
Пример.
Найти интеграл
Решение. Под знаком интеграла неправильная дробь; выделим ее целую часть путем деления числитель на знаменатель:
-
остаток.
Получаем:
Разложим правильную рациональную дробь на простейшие дроби:
т.е.
Отсюда
следует, что
Находим: В=2, А=0, С=4, D=2. т.е.
Интегрируем полученное равенство:
.
Обозначим х+1= t, тогда х = t-1 и dx=dt. Таким образом,
следовательно,
Интегрирование тригонометрических функций
Для
нахождения интегралов типа
используются следующие приемы:
подстановка sin x = t, если n – целое положительное нечетное число;
подстановка cos x = t, если m - целое положительное нечетное число;
формулы понижения порядка:
если
m
и n
– целые неотрицательные четные числа;
подстановка tg x = t, если m + n – есть четное отрицательное целое число.
Пример.
Найти интеграл
Решение.
Применим
подстановку sin
x
= t,
тогда x
= arcsint,
Пример.
Найти интеграл
Решение.
4.6. Определенный интеграл
Если
функция
непрерывна на отрезке
и
- какая-либо ее первообразная на
то
имеет место формула:
(формула Ньютона-Лейбница)
Свойства определенного интеграла
1.
2.
3.
где сє
;
4.
5.
где c
= const.
6. Замена переменной в определенном интеграле осуществляется по формуле
t
– новая переменная,
-
новые пределы интегрирования.
7. Интегрирование по частям в определенном интеграле:
§. Приложения определенного интеграла
Если непрерывная кривая задана в прямоугольных координатах уравнением
,
то площадь
криволинейной трапеции,
ограниченной этой кривой, двумя прямыми
и
и отрезком оси абсцисс
,
определяется формулой
.
Объемы
тел,
образованных вращением вокруг оси Оу
фигуры, ограниченной кривой
,
осью Оу и двумя прямыми
,
можно определить по формуле:
Длина
дуги гладкой
кривой
между двумя точками с абсциссами
Пример.
Найти площадь фигуры, ограниченной
параболой
касательной
к ней в точке (3; 6), и осями координат.
Решение. Найдем уравнение касательной к параболе в точке (3; 6). Угловой
коэффициент
касательной
|
Воспользуемся
уравнением прямой.
Значит, уравнение касательной имеет
вид
Найдем координаты точки С:
Определим
площадь заштрихованной фигуры:
(кв.
ед.).
Пример.
Найти объем тела, образованного при
вращении астроиды
вокруг Ох.
Решение. Астроида симметрична относительно осей Ох и Оу, поэтому
искомый объем равен удвоенному объему тела, получаемого при вращении заштрихованного криволинейного треугольника ОАВ вокруг оси Ох. Находим: |
(куб.
ед).
Пример.
Вычислить длину дуги полукубической
параболы
отсекаемой
прямой х = 5.
Решение.
Указанная дуга состоит из двух частей,
симметричных относительно оси Ох.
Вычислим длину одной из них. Найдем
производную функции
|
и подставим в формулу:
