МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К КОНТРОЛЬНОЙ РАБОТЕ №2
4.4. Функции нескольких переменных.
§ Функции двух переменных
Переменная величина z называется функцией двух переменных величин х и у, если каждой паре допустимых значений х и у соответствует значение Z.
Систему
значений х и у называют точкой
,
а функцию двух переменных – функцией
точки
.
Геометрическим изображением функции двух переменных является некоторая поверхность в пространстве.
§ Частные производные и полный дифференциал функции нескольких переменных.
Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению данной переменной, когда последнее стремиться к нулю.
Для
функции двух переменных
по
определению имеем:
-
частная производная по х;
-
частная производная по у.
При нахождении частной производной пользуются правилами дифференцирования функции одной переменной, считая все другие аргументы постоянными.
Полный
дифференциал функции
вычисляется
по формуле:
Функция имеющая полный дифференциал, называется дифференцируемой.
Пример. Найти частные производные и полный дифференциал функции
Решение. Считая у постоянной и дифференцируя z как функцию х, получаем частную производную по х:
Считая х постоянной и дифференцируя z как функцию у, находим частную производную по у:
Находим полный дифференциал по формуле:
§ Производные и дифференциалы высших порядков.
Частными производными второго порядка функции называются частные производные от ее частных производных первого порядка:
или
Если
смешанные производные
непрерывны, то результаты дифференцирования
не зависят от порядка дифференцирования,
т.е.
.
Аналогично определяются частные производные более высокого порядка.
Дифференциал второго порядка выражается формулой
Пример.
Найти
Решение.
Находим
Формула
полного дифференциала функции применяется
для приближенного вычисления значения
функции
в точке
при достаточно малых
по известным значениям функции
и ее частных производных
в
данной точке
.
Пример.
Вычислить приближенное значение
Решение. Искомое число будем рассматривать как значение функции
Значение
функции в точке (4; 3) равно
Найдем
значения частных производных
в точке (4; 3)
Подставляя в формулу для приближенных вычислений получим
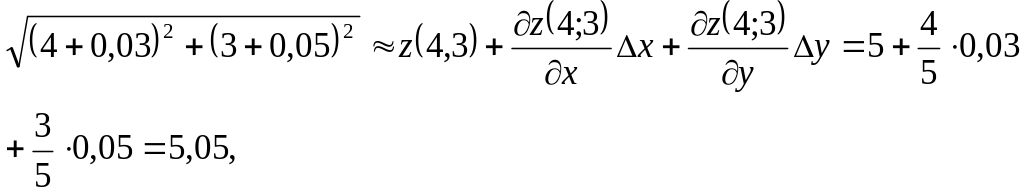следовательно,
§ Экстремум функции нескольких переменных
Максимумом
(минимумом)
функции
называется такое ее значение
,
которое больше (меньше) всех других
значений, принимаемых ею в точках,
достаточно близко к точке
и
отличных от нее.
Максимум или минимум функции называется ее экстремумом.
Экстремум функции нескольких переменных может достигаться лишь в точках, лежащих внутри области ее определения, в которых все частные производные первого порядка обращаются в нуль. Такие точки называются критическими.
Для
функции
критические точки находятся из системы
уравнений:
Пусть точка - критическая точка функции т.е.
Обозначим
(достаточное
условие экстремума), тогда:
если
,
то функция имеет экстремум в точке
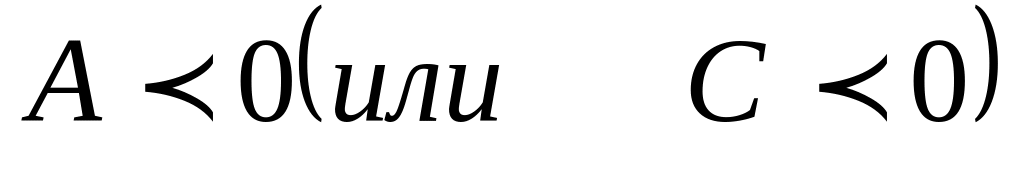причем: максимум при
,
минимум при
.если
,
то экстремума в точке
нет.если
,
то требуется дополнительное исследование.
Пример.
Найти экстремумы функции
Решение. Найдем частные производные функции:
Решим систему:
(0;
3) – критическая точка.
так
как
то точка
(0;
3)- максимум функции. Значение функции
в точке
:
Пример.
Исследовать на экстремум функцию
Решение. Находим частные производные первого и второго порядка:
Приравнивая к нулю первые производные, получим систему уравнений для определения критических точек:
Решая
эту систему находим:
Получены
две критические точки
Вычислим значение частных производных второго порядка в этих точках:
Находим определитель:
Так
как
то в точке
нет
экстремума. В точке
функция имеет максимум, ибо
причем
4.5. Неопределенный интеграл
Множество
всех первообразных функций F(х)
+ С для f(х)
называется неопределенным
интегралом
от функции f(х),
т.е.
Свойства неопределенного интеграла
1)
2)
3)
4)
Таблица основных неопределенных интегралов
1)
10)
2)
11)
3)
12)
4)
13)
5)
14)
6)
15)
7)
16)
8)
17)
9)
18)
