18. Взаимное расположение плоскостей в пространстве: линии пересечения плоскостей, угол между плоскостями.

Возможны два случая взаимного расположения двух плоскостей в пространстве:

• Параллельны

• Пересекаться

Перпендикулярные плоскости: Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.

Линией пересечения двух плоскостей является прямая, для построения которой достаточно определить две её точки, общие обеим плоскостям, либо одну точку и направление линии пересечения плоскостей.

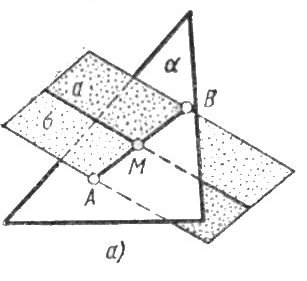
У гол между плоскостями

Рассмотрим две плоскости α₁ и α₂, заданные соответственно уравнениями:

Под углом между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между нормальными векторами и плоскостей α₁ и α₂ равен одному из указанных смежных двугранных углов или . Поэтому 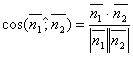. Т.к. и , то

.

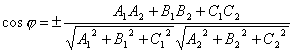Пример. Определить угол между плоскостями x+2y-3z+4=0 и 2x+3y+z+8=0.

Условие параллельности двух плоскостей.

Две плоскости α₁ и α₂ параллельны тогда и только тогда, когда их нормальные векторы и параллельны, а значит .

Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:

или

Условие перпендикулярности плоскостей.

Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, или .

Таким образом,

19.Расстояние от точки до плоскости, угол между прямой и плоскостью

Расстояние от точки до плоскости равно длине перпендикуляра, опущенного из точки на эту плоскость. Пусть требуется найти расстояние от точки K до плоскости  (АВС)

Алгоритм построения:

1. Строится перпендикуляр из точки K на плоскость  (АВС) : m₁ h₁, m₂ f₂.

2. Находится точка N - точка пересечения перпендикуляра m с плоскостью  (АВС).

3. Определяется расстояние от точки K до точки N с помощью прямоугольного треугольника K₁N₁M₀. Длина гипотенузы N₁M₀ – это искомое расстояние: |KN| = N₁M₀.

Расстояние между параллельными плоскостями определяется длиной перпендикуляра, опущенного из произвольной точки одной плоскости до другой. Аналогично находится расстояние от плоскости до параллельной ей прямой. На прямой берется точка и находится расстояние до плоскости.

Угол между прямой и плоскостью

Дана плоскость и точка А вне этой плоскости.

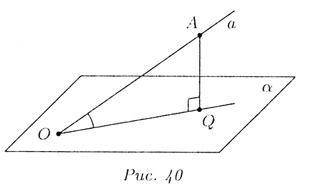
Проекцией точки А на плоскость называется основание Q перпендикуляра, проведенного из этой точки к плоскости.

Пусть а — произвольная прямая, пересекающая плоскость в точке О, причем прямая а не перпендикулярна плоскости (рис. 40).

Прямая а и перпендикуляр AQ (А € а) определяют плоскость , _|_ .

Прямая a₁, проходящая через точки О и Q, называется проекцией а на плоскость .

Углом между прямой а и плоскостью , пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой а и ее проекцией a₁ на плоскость (рис. 40).

Если прямая а перпендикулярна плоскости , то ее проекцией на плоскость представляет собой точку О, а угол между а и считается прямым (равным 90°).

Если прямая а параллельна плоскости , то угол между ними принимают равным нулю.