16.Общее уравнение плоскости и уравнение плоскости в отрезках. Нахождение общего уравнения плоскости по трем точкам, принадлежащим плоскости.

Плоскостью называется поверхность, все точки которой удовлетворяют общему уравнению:

 Ax + By + Cz + D = 0

Возможны следующие частные случаи:

А = 0 – плоскость параллельна оси Ох

В = 0 – плоскость параллельна оси Оу

С = 0 – плоскость параллельна оси Оz

D = 0 – плоскость проходит через начало координат

А = В = 0 – плоскость параллельна плоскости хОу

А = С = 0 – плоскость параллельна плоскости хОz

В = С = 0 – плоскость параллельна плоскости yOz

А = D = 0 – плоскость проходит через ось Ох

В = D = 0 – плоскость проходит через ось Оу

С = D = 0 – плоскость проходит через ось Oz

А = В = D = 0 – плоскость совпадает с плоскостью хОу

А = С = D = 0 – плоскость совпадает с плоскостью xOz

В = С = D = 0 – плоскость совпадает с плоскостью yOz

 Уравнение плоскости в отрезках

где a, b, c - величины отрезков, отсекаемых плоскостью на осях координат.

Стандартное уравнение плоскости -

Ax + By + Cz + D = 0

Вектор (A, B, C) перпендикулярен плоскости.

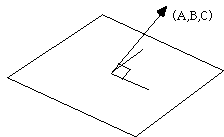
Уравнение плоскости по трем точкам (x1,y1,z1), (x2,y2,z2), (x3,y3,z3) можно получить из следующих опрееделителей:

Раскрывая, получаем

A = y1 (z2 - z3) + y2 (z3 - z1) + y3 (z1 - z2)

B = z1 (x2 - x3) + z2 (x3 - x1) + z3 (x1 - x2)

C = x1 (y2 - y3) + x2 (y3 - y1) + x3 (y1 - y2)

- D = x1 (y2 z3 - y3 z2) + x2 (y3 z1 - y1 z3) + x3 (y1 z2 - y2 z1)

Следует заметить, что, если все точки лежат на одной прямой, то (A,B,C) будет (0,0,0).

Знак s = Ax + By + Cz + D определяет, с какой стороны по отношению к плоскости находится точка (x,y,z). Если s > 0, то точка лежит в той стороне, куда указывает нормальный вектор (A,B,C). Если s < 0 - на противаположной стороне, а в случае s = 0 точка принадлежит плоскости.

17.Параметрическое и каноническое уравнение прямой в пространстве

• Параметрические уравнения прямой в пространстве:

(**)

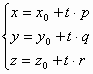Вы никогда не сталкивались с параметрическим заданием кривых? Поясним на примере: представьте себе, что по заранее намеченному маршруту с известной скоростью движется турист (автомобиль, самолёт, подводная лодка, как Вам больше понравится). Тогда, зная точку начала его путешествия, мы в любой момент времени знаем, где он находится. Таким образом, его положение на маршруте определяется всего одним параметром – временем.

В нашем случае турист движется по бесконечной прямой в пространстве, в момент времени t₀=0 он находится в точке М₀, в любой другой момент времени t его координаты в пространстве вычисляются по формулам (**).

Теперь несколько преобразуем формулы (**).

Выразим из каждой строчки параметр t:

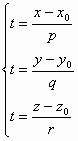
• Канонические уравнения прямой в пространстве:

Замечание 2: Эта компактная запись на самом деле содержит три уравнения.

Замечание 3: Это формальная запись и выражение вида в данном случае допустимо.

Замечание 4: Надо понимать, что для уравнения плоскости (прямой) играет роль именно направление перпендикулярного (направляющего) вектора, а не он сам. Т.о. вполне допустимо из каких-либо соображений заменять данный (или полученный в ходе решения) вектор на пропорциональный ему. Целесообразно также упрощать полученное уравнение, деля все его коэффициенты на общий множитель.