11. Декартова система координат в , базис и его особенности (ортонормированность).
Декартова прямоугольна система координат в пространстве определяется заданием линейной единицы для измерения длин и трех пересекающихся в одной точке взаимно перпендикулярных осей, занумерованных в каком-либо порядке.
Точка пересечения осей называется началом координат, а сами оси - координатными осями. Первая координатная ось называется осью абсцисс, вторая - осью ординат, третья - осью апликат.
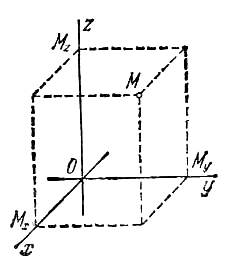
Ба́зис— множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества - базисных векторов.
В случае, когда базис бесконечен, понятие «линейная комбинация» требует уточнения. Это ведёт к двум основным разновидностям определения:
Базис Га́меля, в определении которого рассматриваются только конечные линейные комбинации. Базис Гамеля применяется в основном в абстрактной алгебре (в частности в линейной алгебре).
Базис Ша́удера, в определении которого рассматриваются и бесконечные линейные комбинации, а именно — разложение в ряды. Это определение применяется в основном в функциональном анализе, в частности для гильбертова пространства,
В конечномерных пространствах обе разновидности базиса совпадают.
Базис ортогональный и ортонормированный. Их построение.
Базис e1, e2, … , en в n –мерном евклидовом пространстве En называется ортогональным, если (ei, ej) = 0 "i ≠ j , т.е. все векторы попарно ортогональны.
Ортогональный базис из единичных векторов называется ортонормированным.
Лемма. Попарно ортогональные и отличные от нуля векторы линейно независимы.
Теорема. В любом евклидовом пространстве существует ортонормированный базис.
Два
вектора называются ортогональными
(перпендикулярными),
если угол между ними прямой (величина 
угла
равна 
).
Система векторов называется ортогональной, если все векторы, образующие ее, попарно ортогональны. Система векторов называется ортонормировинной, если она ортогональная и длина каждого вектора равна единице.
Определение.
Тройка векторов 
называется
ортогональной, если эти векторы попарно
ортогональны друг другу, т.е. 
, 
.
Определение.
Тройка векторов
называется
ортонормированной, если она ортогональная
и длины всех векторов равны
единице: 
.
Если
в ортогональном базисе все вектора
имеют норму =1, то он называется
ортонормированным.
норма
х=корень из скалярного квадрата.
12. Линейные операции с векторами в пространстве (сложение, умножение на число).
13.Скалярное произведение векторов в пространстве . Угол между прямыми.
14.Длина вектора в пространстве , . Обобщение длины – норма вектора в .
Евклидово пространство:
Определение
Действительное
линейное пространство E
называется евклидовым, если каждой
паре векторов
сопоставляется
число
так,
что
и
выполняются
аксиомы:
I.
II.
III.
IV.
Число
называют
скалярным произведением векторов
и,
-
скалярным квадратом вектора
(пишут
).
Введенная операция называется скалярным
умножением векторов
и
.
Длина вектора
Длина
вектора
-
число
Свойства:
1)
2)
3)
(неравенство
Коши-Буняковского);
4)
(неравенство
треугольника).
Углом
между векторами
и
называют
угол
,
для которого
Ортогональные векторы
Векторы
ортогональны,
если
Нормированные векторы
Вектор
называется
нормированным или единичным, если
Если
то
соответствующими этому вектору
нормированными векторами будут
Нормой (длиной) вектора x Î E называется число, равное √
(x, x)
и обозначаемое || x || .
Из аксиом скалярного произведения следуют свойства нормы:
1. || x || >0 "x ≠ θ ;
2. || x || = 0 ÜÞ x = θ .
3. || x + y || ≤ || x || + || y || .
Вектор, норма которого равна единице, называется единичным (нормированным) вектором, или ортом.
Расстоянием между векторами x Î E и y Î E называется норма их разности, т.е. || x − y || .
Теорема. Для любых векторов x, y Î E справедливо неравенство Коши–Буняковского:
| (x, y) | ≤ || x || • || y || .
Доказательство см. в книге О.В. Зиминой ``Линейная алгебра и аналитическая геометрия".
Углом между ненулевыми векторами x Î E и y Î E называется угол j такой, что
cosj =
(x,y)
|| x || • || y ||