7. Линии уровня поверхностей и их интерпретация.

Уровня линии (поверхности), множества точек, в которых функция и (Р) точки Р плоскости (пространства) принимает постоянные значения. Уравнение u (P) = const в двумерной области определяет линию (линию уровня), в трёхмерной области √ поверхность (поверхность уровня). Изображение функций с помощью У. л. (п.) широко применяется в метеорологии (изотермы, изобары и т.д.), геодезии и топографии (горизонтали) и др. науках. У. л.(п.) в точках экстремума функции и (Р) вырождаются в точки. Градиент функции u (Р) перпендикулярен У. л. (п.) в соответствующей точке.

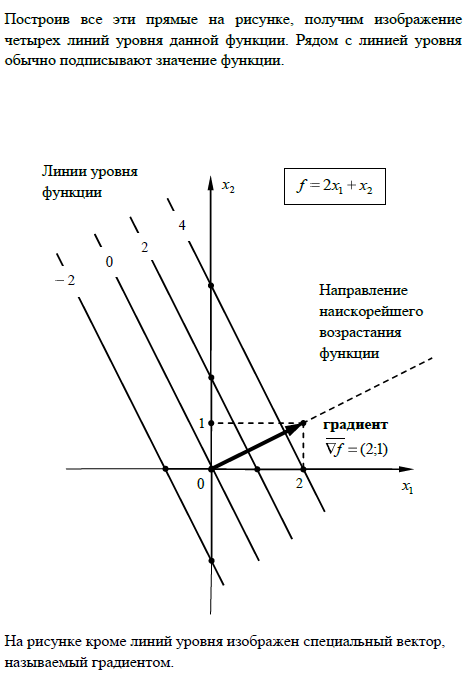
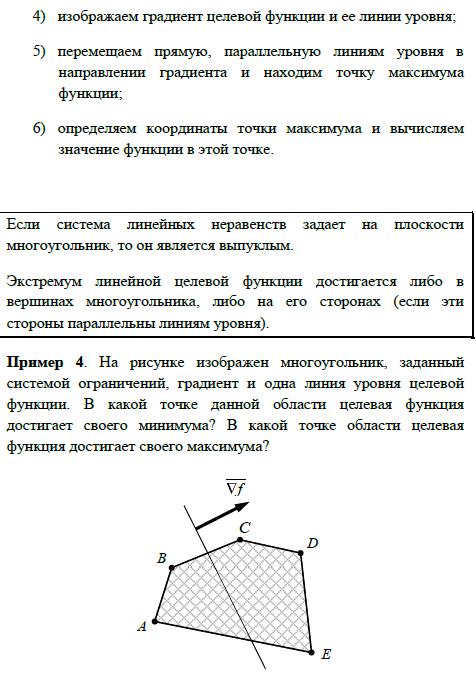
8.Постановка и графическое решение задачи линейного программирования с двумя переменными.

9. Кривые второго порядка на плоскости: общее уравнение, каноническая форма и графики кривых в канонической системе координат.

10. Определение и геометрические свойства эллипса, гиперболы и параболы

Эллипс, геом. замкнутая кривая линия, получаемая от пересечения конуса плоскостью, непараллельной основанию; внутри Э. находятся две точки (фокусы), сумма расстояний которых от каждой точки кривой (радиусы=векторы) есть величина постоянная, равная большей оси (большому диаметру) Э. Диаметр, перпендикулярный к большой оси и делящий ее на две равные части, наз. малой осью Э. Отношение расстояния между фокусами к большой оси назыв. эксцентриситетом. Орбиты планет суть Э.

Парабола, линия пересечения круглого конуса плоскостью, параллельной какой-либо касательной плоскости этого конуса (рис. 1). П. может быть также определена как геометрическое место точек плоскости (рис. 2), для каждой из которых расстояние до определённой точки F плоскости — фокуса П.— равно расстоянию до некоторой прямой MN — директрисы П. Прямая, проходящая через фокус перпендикулярно директрисе и направленная от директрисы к фокусу, называется осью П., а точка пересечения оси с П.— вершиной П. Если выбрать систему координат хОу так, как указано на рис. 2, то уравнение П. примет вид:

у² = 2рх,

где р — длина отрезка FN. Величина р называется параметром П. Парабола — линия второго порядка. График квадратного трёхчлена у = ax² + bx + c является П. Парабола представляет собой бесконечно простирающуюся кривую, симметричную относительно оси. Если в фокусе П. поместить источник света, то лучи, отразившиеся от П., образуют параллельный пучок, т.к. прямая PF, соединяющая любую точку Р П. с фокусом, и прямая, параллельная оси, образует с нормалью PR равные углы. Это свойство П. применяется, например, для прожекторных устройств (см. Параболическая антенна). См. также Конические сечения.

гипербола это плоская кривая второго порядка, которая состоит из двух отдельных кривых, которые не пересекаются. Формула гиперболы У=К/х, при условии, что к не равно 0. Тоесть вершины гиперболы стремятся к нолю, но никогда не пересекаются с ним.

Второе значение - литературное. Гипербола это стилистическая фигура намеренного преувеличения.

Пространство