
- •Декартова система координат на плоскости, векторы на плоскости и операции с ними.
- •* Операции над векторами:
- •2. Скалярное произведение и проекции векторов на плоскости.
- •3. Прямая на плоскости: методы задания, виды уравнений и смысл коэффициентов
- •4. Взаимное расположение прямых на плоскости: пересечение прямых, угол между прямыми.
- •5. Расстояние от точки до прямой.
- •7. Линии уровня поверхностей и их интерпретация.
- •8.Постановка и графическое решение задачи линейного программирования с двумя переменными.
- •9. Кривые второго порядка на плоскости: общее уравнение, каноническая форма и графики кривых в канонической системе координат.
- •10. Определение и геометрические свойства эллипса, гиперболы и параболы
- •11. Декартова система координат в , базис и его особенности (ортонормированность).
- •12. Линейные операции с векторами в пространстве (сложение, умножение на число).
- •13.Скалярное произведение векторов в пространстве . Угол между прямыми.
- •14.Длина вектора в пространстве , . Обобщение длины – норма вектора в .
- •15.Векторное произведение : геометрическая интерпретация и формула вычисления.
- •16.Общее уравнение плоскости и уравнение плоскости в отрезках. Нахождение общего уравнения плоскости по трем точкам, принадлежащим плоскости.
- •17.Параметрическое и каноническое уравнение прямой в пространстве
- •18. Взаимное расположение плоскостей в пространстве: линии пересечения плоскостей, угол между плоскостями.
- •У гол между плоскостями
- •19.Расстояние от точки до плоскости, угол между прямой и плоскостью
- •Угол между прямой и плоскостью
- •20. Поверхности второго порядка: канонические уравнения и виды поверхностей
- •28.Обратная матрица: определение и 2 метода вычисления
- •29.Классификация слау в зависимости от числа линейно-независимых уравнений и числа неизвестных, теорема Кронекера-Капелли о совместности слау.
- •Достаточность:
- •30.Решение слау методом Крамера.
- •31.Решение слау методом Гаусса.
5. Расстояние от точки до прямой.
|
6. Системы линейных неравенств и графическая интерпретация их решений на плоскости.
Линейное неравенство - неравенство, левая и правая части которого - линейные функции относительно неизвестных.
ЛИНЕЙНОЕ НЕРАВЕНСТВО
неравенство вида
![]()
или вида
![]()
где
![]() а-
любые действительные числа, В
а-
любые действительные числа, В
![]() более
широком смысле - это неравенство вида
более
широком смысле - это неравенство вида
![]()
или вида
![]()
где
f(x) - линейная (т. е. аддитивная и однородная)
функция на действительном векторном
пространстве
![]()
Графический метод
Графический метод заключается в построении множества допустимых решений ЗЛП, и нахождении в данном множестве точки, соответствующей max/min целевой функции.
В связи с ограниченными возможностями наглядного графического представления данный метод применяется только для систем линейных неравенств с двумя неизвестными и систем, которые могут быть приведены к данному виду.
Для того чтобы наглядно продемонстрировать графический метод, решим следующую задачу:
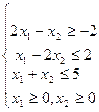
![]()
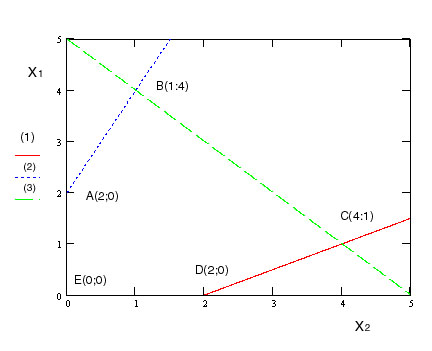
На первом этапе надо построить область допустимых решений. Для данного примера удобнее всего выбрать X2 за абсциссу, а X1 за ординату и записать неравенства в следующем виде:
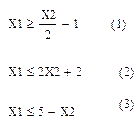
Так
как
![]() и
и
![]() графики
и область допустимых решении находятся
в первой четверти.
графики
и область допустимых решении находятся
в первой четверти.
Для того чтобы найти граничные точки решаем уравнения (1)=(2), (1)=(3) и (2)=(3).
Как видно из иллюстрации многогранник ABCDE образует область допустимых решений.
Если область допустимых решений не является замкнутой, то либо max(f)=+ ∞, либо min(f)= -∞.
Теперь можно перейти к непосредственному нахождению максимума функции f.
Поочерёдно подставляя координаты вершин многогранника в функцию f и сравнивать значения, находим что
f(C)=f(4;1)=19 – максимум функции.
Такой подход вполне выгоден при малом количестве вершин. Но данная процедура может затянуться если вершин довольно много.
В таком случае удобнее рассмотреть линию уровня вида f=a. При монотонном увеличении числа a от -∞ до +∞ прямые f=a смещаются по вектору нормали[1]. Если при таком перемещении линии уровня существует некоторая точка X – первая общая точка области допустимых решений (многогранник ABCDE) и линии уровня, то f(X)- минимум f на множестве ABCDE. Если X- последняя точка пересечения линии уровня и множества ABCDE то f(X)- максимум на множестве допустимых решений. Если при а→-∞ прямая f=a пересекает множество допустимых решений, то min(f)= -∞. Если это происходит при а→+∞, то
max(f)=+ ∞.
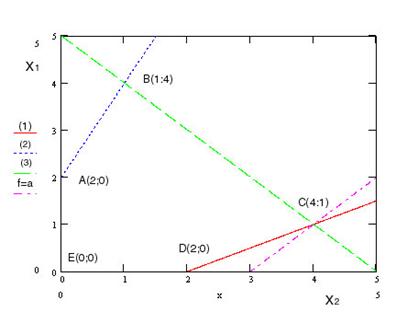
В нашем примере прямая f=a пересевает область ABCDE в точке С(4;1). Поскольку это последняя точка пересечения, max(f)=f(C)=f(4;1)=19.
Симплекс-метод
Реальные задачи линейного программирования содержат очень большое число ограничений и неизвестных и выполняются на ЭВМ. Симплекс-метод – наиболее общий алгоритм, использующийся для решения таких задач. Суть метода заключается в том, что после некоторого числа специальных симплекс- преобразований ЗЛП, приведенная к специальному виду, разрешается.
Метод искусственного базиса
Если после подготовки ЗЛП к специальному виду для решения симплекс методом, не в каждой строке системы ограничений есть базисная переменная (входящая в данную строку с коэффициентом 1, а в остальные строки с коэффициентом 0), то для решения данной ЗЛП надо воспользоваться методом искусственного базиса.
Суть метода довольно проста:
К строкам, в которых отсутствует базисная переменная добавляется по одной искусственной базисной переменной.
Новая задача решается Симплекс-методом, причем все искусственные базисные переменные должны стать свободными (выйти из базиса) и их сумма должна равняться нулю, в обратном случае в данной системе невозможно выделить допустимый базис.

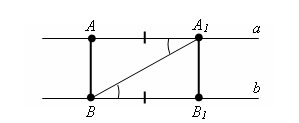 Пусть
а и b – параллельные прямые и точки
A и A1 – некоторые точки на прямой a.
Опустим из точки A перпендикуляр AB
на прямую b и отложим из точки B
отрезок BB1, равный AA1 так, что бы A и
B1 были по разные стороны от прямой
A1B.
Δ A1AB = Δ BB1A1 по первому признаку
равенства треугольников (A1B – общая,
∠
AA1B = ∠
B1BA1 – как внутренние накрест лежащие,
AA1=B1B).
Из равенства треугольников
следует, что A1B1 тоже перпендикуляр
к прямой b и AB = A1B1. Теорема доказана.
Расстоянием
между параллельными прямыми
называется расстояние
от какой-нибудь точки одной прямой
до другой прямой.
Пусть
а и b – параллельные прямые и точки
A и A1 – некоторые точки на прямой a.
Опустим из точки A перпендикуляр AB
на прямую b и отложим из точки B
отрезок BB1, равный AA1 так, что бы A и
B1 были по разные стороны от прямой
A1B.
Δ A1AB = Δ BB1A1 по первому признаку
равенства треугольников (A1B – общая,
∠
AA1B = ∠
B1BA1 – как внутренние накрест лежащие,
AA1=B1B).
Из равенства треугольников
следует, что A1B1 тоже перпендикуляр
к прямой b и AB = A1B1. Теорема доказана.
Расстоянием
между параллельными прямыми
называется расстояние
от какой-нибудь точки одной прямой
до другой прямой.