Плоскость
Декартова система координат на плоскости, векторы на плоскости и операции с ними.
*Прямоугольная (Декартовая) система координат на плоскости:
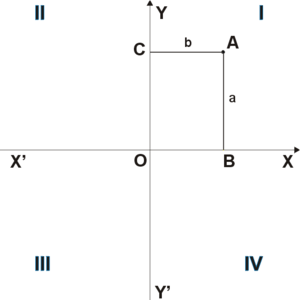
Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат OX и OY. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление. В правосторонней системе координат положительное направление осей выбирают так, чтобы при направлении оси OY вверх, ось OX смотрела направо.
Четыре угла (I, II, III, IV), образованные осями координат X'X и Y'Y, называются координатными углами или квадрантами (см. рис. 1).
Положение
точки A
на плоскости определяется двумя
координатами x
и y.
Координата x
равна длине отрезка OB,
координата y —
длине отрезка OC
в выбранных единицах измерения. Отрезки
OB
и OC
определяются линиями, проведёнными из
точки A
параллельно осям Y'Y
и X'X
соответственно. Координата x
называется абсциссой
точки A,
координата y —
ординатой
точки A.
Записывают так:
.
Если точка A лежит в координатном углу I, то точка A имеет положительные абсциссу и ординату. Если точка A лежит в координатном углу II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном углу III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном углу IV, то точка A имеет положительную абсциссу и отрицательную ординату
*Векторы на плоскости и операции с ними:
Вектором называеться направленный отрезок(отрезок,у которого одна граничная точка считается начальной, другая - конечной). Над буквенным обозначением вектора ставится стрелка. Длиной вектора называеттся расстояние между началом и концом вектора. Нулевым называется вектор,у которого начало и конец равны нулю. Его направление не определено. Два ненулевых вектора, лежащих на одной прямой или на параллельных прямых, называются коллинеарными. Нулевой коллинеарен любому вектору.
Вектор, длина которого равна единице,называется единичным вектором. Векторы называют равными,если они коллинеарны,имеют одинаковую длину и направление. Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если тройка векторов содержит нулевой вектор или пару коллинеарных векторов,то эти векторы компланарны. Векторы называют противоположными, если их длины равны,а направления противоположны. Суммой векторов, расположенных так,что начало 1ого вектора совпадает с концом 2ого вектора, называется 3ий вектор, начало которого совпадает с началом 1ого вектора, а конец- с концом 2ого вектора. Вектор с называется разностью векторов а и б , если с+б=а. Отсюда следует,что с = а+(-б), т.е. вычитание векторов сводится к их сложению. Произведением вектора с на число н,называется такой вектор с, что модуль с = модуль н * а, а направление его совпадает с направление вектора а, если н>0, и ему противоположно, если число меньше 0; если а равно нулю и число = 0, то их произведение = 0.