
8Вопрос
Вектор – это направленный отрезок, то есть такой отрезок, у которого есть начало и конец:
Линейными операциями называют операции сложения и вычитания векторов и умножения вектора на число.
Сложение
векторов. Пусть ![]() и
и ![]() –
два произвольных вектора. Возьмем
произвольную точку О и
построим вектор
–
два произвольных вектора. Возьмем
произвольную точку О и
построим вектор ![]() ;
затем от точки А отложим
вектор
;
затем от точки А отложим
вектор ![]() .
Вектор
.
Вектор ![]() ,
соединяющий начало первого слагаемого
вектора с концом второго, называется суммой этих
векторов и обозначается
,
соединяющий начало первого слагаемого
вектора с концом второго, называется суммой этих
векторов и обозначается ![]()
Вычитание
векторов. Разностью ![]() векторов
и
называется
такой вектор
векторов
и
называется
такой вектор ![]() ,
который в сумме с вектором
дает
вектор
:
,
который в сумме с вектором
дает
вектор
: ![]() Û
Û ![]() .
.
Если векторы и привести к общему началу, то разность представляет собой отрезок, соединяющий их концы и направленный от «вычитаемого» к «уменьшаемому»
Умножение
вектора на число. Произведением вектора
на
действительное число ![]() называется
вектор
(обозначают
называется
вектор
(обозначают ![]() ),
определяемый следующими условиями:
),
определяемый следующими условиями:
1) ![]() ,
,
2) ![]() при
при ![]() и
и ![]() при
при ![]() .
.
Очевидно,
что при ![]()
![]() .
.
Свойства линейных операций:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
; ![]() ;
;
4) ![]() ;
;
5) ![]() ;
;
6) ![]() ;
;
7) ![]() ;
; ![]() ;
;
9Вопрос
Координатами
вектора ![]() называются
проекции
называются
проекции ![]() и
и ![]() данного
вектора на оси
данного
вектора на оси ![]() и
и ![]() соответственно:
соответственно:
![]()
Величина
называется абсциссой
вектора
,
а число
-
его ординатой.
То, что вектор
имеет
координаты
и
,
записывается следующим образом: ![]() .
.
Чтобы найти сумму двух векторов, заданных своими координатами, надо сложить их соответствующие координаты.
Чтобы умножить вектор на число, надо каждую координату этого вектора умножить на заданное число.
Чтобы найти координаты вектора, заданного координатами начала и конца, надо от координат конца отнять соответствующие координаты начала.
Направляющими косинусами вектора называются косинусы углов, образованных вектором с положительными направлениями осей координат.
Сумма квадратов направляющих косинусов равна единице.
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому вектору.
два
ненулевых вектора ![]() и
и ![]() коллинеарны
тогда и только тогда, когда их векторное
произведение равно нулевому вектору.
коллинеарны
тогда и только тогда, когда их векторное
произведение равно нулевому вектору.
Единичный вектор - это вектор, абсолютная величина (модуль) которого равен единице. Для обозначения единичного вектора мы будем использовать нижний индекс е. Так, если задан вектор а, то его единичным вектором будет вектор ае. Этот единичный вектор направлен туда же, куда направлен и сам вектор а, и его модуль равен единице, то есть ае = 1.
Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными.
Условия коллинеарности векторов
Два вектора коллинеарные, если отношения их координат равны.
Два вектора коллинеарные, если их векторное произведение равно нулю.
10Вопрос
Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.
Скалярное
произведение векторов ![]() ,
, ![]() обозначается
символом
обозначается
символом ![]() (порядок
записи сомножителей безразличен, то
есть
(порядок
записи сомножителей безразличен, то
есть ![]() ).
).
Если
угол между векторами
,
обозначить
через ![]() ,
то их скалярное произведение можно
выразить формулой
,
то их скалярное произведение можно
выразить формулой
![]() (1)
(1)
Скалярное произведение векторов , можно выразить также формулой
![]() ,
или
,
или ![]() .
.
Из
формулы (1) следует, что ![]() ,
если
-
острый угол,
,
если
-
острый угол, ![]() ,
если
-
тупой угол;
,
если
-
тупой угол; ![]() в
том и только в том случае, когда
векторы
и
перпендикулярны
(в частности,
,
если
в
том и только в том случае, когда
векторы
и
перпендикулярны
(в частности,
,
если ![]() или
или ![]() ).
).
Скалярное
произведение ![]() называется
скалярным квадратом вектора и обозначается
символом
называется
скалярным квадратом вектора и обозначается
символом ![]() .
Из формулы (1) следует, что скалярный
квадрат вектора равен квадрату его
модуля:
.
Из формулы (1) следует, что скалярный
квадрат вектора равен квадрату его
модуля:
![]() .
.
Если векторы и заданы своими координатами:
![]() ,
, ![]() ,
,
то их скалярное произведение может быть вычислено по формуле
![]() .
.
Отсюда следует необходимое и достаточное условие перпендикулярности двух векторов
![]() .
.
Угол между векторами
, ,
дается
формулой  ,
или в координатах
,
или в координатах
![]() .
.
Проекция
произвольного вектора ![]() на
какую-нибудь ось u определяется
формулой
на
какую-нибудь ось u определяется
формулой
![]() ,
,
где ![]() -
единичный вектор, направленный по оси u.
Если даны углы
-
единичный вектор, направленный по оси u.
Если даны углы ![]() ,
, ![]() ,
, ![]() ,
которые оси u составляет с
координатными осями, то
,
которые оси u составляет с
координатными осями, то ![]() и
для вычисления вектора
и
для вычисления вектора ![]() может
служить формула
может
служить формула
![]() .
.
свойство коммутативности скалярного произведения
 ;
;свойство дистрибутивности
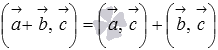 или
или  ;
;сочетательное свойство
 или
или  ,
где
,
где  -
произвольное действительное число;
-
произвольное действительное число;скалярный квадрат вектора всегда не отрицателен
 ,
причем
,
причем 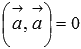 тогда
и только тогда, когда вектор
тогда
и только тогда, когда вектор  нулевой.
нулевой.
Решение различных задач на вычисление скалярного произведения векторов сводится к использованию свойств скалярного произведения и формул
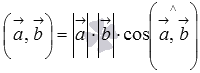 ;
; ;
; или
или 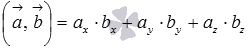 ;
; .
.
