
1Вопрос
Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы.
Прямоугольной матрицей размера m´n называется совокупность mn чисел, расположенных в виде прямоугольной таблицы, содержащей m строк и n столбцов. Мы будем записывать матрицу в виде

Матрицей будем называть любую прямоугольную таблицу, составленную из чисел aij
Матрица, состоящая из одной строки или одного столбца, называется соответственно вектор-строкой или вектор-столбцом. Вектор-столбцы и вектор-строки называют просто векторами.
Матрица, состоящая из одного числа, отождествляется с этим числом. Матрица размера m´n, все элементы которой равны нулю, называются нулевой матрицей и обозначается через 0. Элементы матрицы с одинаковыми индексами называют элементами главной диагонали. Если число строк матрицы равно числу столбцов, то есть m = n, то матрицу называют квадратной порядка n. Квадратные матрицы, у которых отличны от нуля лишь элементы главной диагонали, называются диагональными матрицами и записываются так:
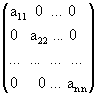 .
.
Если все элементы a i i диагональной матрицы равны 1, то матрица называется единичной и обозначается буквой Е:
 .
.
Квадратная матрица называется треугольной, если все элементы, стоящие выше (или ниже) главной диагонали, равны нулю. Транспонированием называется такое преобразование матрицы, при котором строки и столбцы меняются местами с сохранением их номеров. Обозначается транспонирование значком Т наверху.
2Вопрос
Определителем второго порядка (соответствующим данной матрице) называется число
![]()
Свойства определителей второго порядка:
1. Определитель не изменится, если его строки поменять местами с соответствующими столбцами.
2. При перестановке двух строк (или столбцов) определитель изменит знак на противоположный, сохраняя абсолютную величину
3. Определитель с двумя одинаковыми строками и столбцами равен нулю.
4. Общий множитель всех элементов строки или столбца можно выносить за знак определителя; если все элементы какой-то строки или столбца равны 0, то и определитель равен 0.
5. Если к элементам какой либо строки (или столбца) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель не изменит своей величины.
Свойство 1. Если все элементы какой-либо строки (столбца) определителя 3-го порядка равны нулю, то и определитель равен нулю. Свойство 2. Определитель 3-го порядка не изменится, если его строки заменить столбцами с теми же номерами. Свойство 3. Если поменять местами две строки (столбца) определителя 3-го порядка, то обсолютная величина определителя не изменится, а знак изменится на противоположный Следствие. Определитель 3-го порядка, в котором каких-либо две строки (столбца) совпадают, равен нулю. Свойство 4. Если все элементы какой-либо строки (столбца) определителя 3-го порядка умножить на какое-либо число, то и определитель умножится на это число. Следствие 1. Если все элементы какой-либо строки (столбца) имеют общий множитель, то этот множитель можно вынести за знак определителя. Следствие 2. Если все элементы какой-либо строки (столбца) определителя 3-го порядка пропорциональны соответствующим элементам другой строки (столбца) этого определителя, то определитель равен нулю. Свойство 5. Если каждый элемент какой-либо строки (столбца) определителя 3-го порядка представляет собой сумму двух слагаемых, то и определитель можно представить в виде суммы двух слагаемых, например:
|
|||||||||||||||||||||||||||||||||||||||||||
Следствие. Если какая - либо строка (столбец) определителя 3-го порядка представляет собой линейную комбинацию двух остальных строк (столбцов), то определитель равен нулю. |
