Случайные процессы

Реально бОльшая часть систем и устройств находится под воздействием неизвестных факторов. Поскольку с течением времени действия этих факторов меняются, то предсказать поведение исследуемых процессов заранее также невозможно. Величины, которые приводились в примерах, представляют собой случайные функции времени. В результате конкретного опыта случайная функция превратится в обычную неслучайную.

Во втором примере состояние системы не характеризуется числовой величиной, а описывается качественно: процесс функционирования этой системы сводится к случайной смене состояний и блужданию по состоянию.

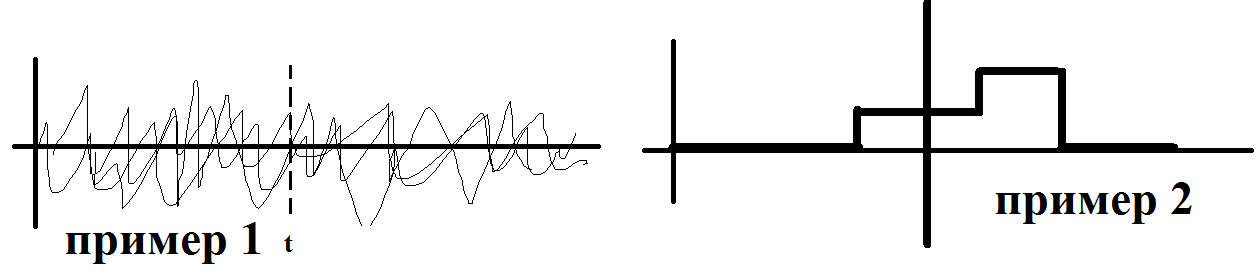
При фиксируемом t случайное состояние системы превращается в аналог случайного события. Случайным процессом X(t) называется процесс, значение которого при любом фиксированном t является случайной величиной.

Случайная величина 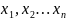, в которую обращается случайный процесс при фиксируемом t называется сечением случайного процесса.

После реализации опыта случайный процесс превращается в неслучайную функцию, которая называется реализацией случайного процесса.

Случайный процесс является обобщением понятия случайной величины на тот случай, когда условия опыта непостоянны, меняются.

Классификация сп

По времени:

СП называется процессом с дискретным временем, если он может менять свои состояния только в моменты t, число которых дискретно или счетно.

СП называется процессом с непрерывным временем, если переходы из состояния в состояние могут происходить в любой момент времени.

По состоянию:

СП называется процессом с непрерывным состоянием, если его сечение в момент времени t представляет собой непрерывную случайную величину.

СП называется процессом с дискретными состояниями, если в момент времени t может быть только конечный набор состояний.

Все процессы с качественными состояниями представляют собой СП с дискретными состояниями. Сечение такого процесса – случайное событие. Пример:

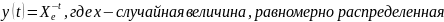
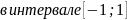; x→R[-1;1]

Характеристики сп

Пусть задан СП X(t).

При фиксируемом t мы получаем случайную величину x. для нее:

• F(x) = P{X<x} – функция распределения

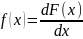• плотность распределения

Это т.н. одномерный закон распределения. Наиболее полное описание дает n-мерная плотность распределения случайных величин, полученных по сечениям в различный момент времени. Для более простого описания СП вводится понятие числовых характеристик, которые для случайного процесса представляют собой детерминированные функции времени.

Математическим ожидание СП X(t) называется такая неслучайная функция m_x(t), которая при любом значении t равна математическому ожиданию соответствующего сечения СП.

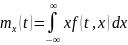
Дисперсией СП X(t) называется такая неслучайная функция dx(t), которая при любом значении t равна дисперсии соответствующего сечения СП.

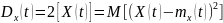
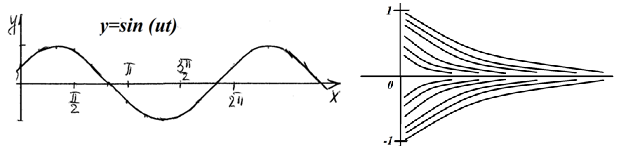
На самом деле данные числовые характеристики не исчерпывают свойства СП, поскольку опреляются лишь одномерным законом. Рассмотрим 2 примера:

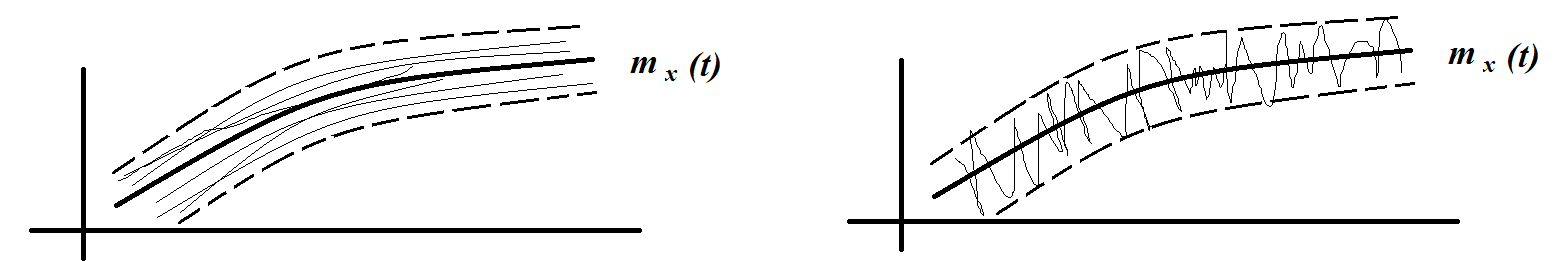
Процесс, изображенный на примере 1 от одного сечения к другому протекает сравнительно плавно, а процесс на примере 2 обладает сильной изменчивостью от сечения к сечению. Поэтому статистическая связь между сечениями в первом случае больше, чем во втором, однако ни по математическому ожиданию, ни по дисперсии этого установить нельзя.

Чтобы в какой-то мере охарактеризовать внутреннюю структуру случайного процесса, т. е. учесть связь между значениями случай­ного процесса в различные моменты времени или, иными словами, учесть степень изменчивости случайного процесса, необходимо ввести понятие о корреляционной (автокорреляционной) функции случай­ного процесса.

Корреляционной функцией случайного процесса X(t) называют не­случайную функцию двух аргументов R_x(t₁, t₂), которая для каждой пары произвольно выбранных значений аргументов (моментов времени) t₁ и t₂ равна математическому ожиданию произведения двух случайных величин X(t₁) и X(t₂) соответствующих сечений случайного процесса:

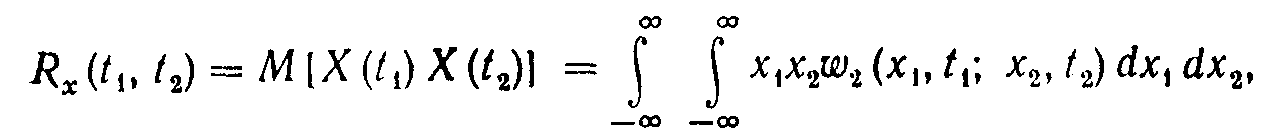(6.1)

где ₂(x₁, t₁; x₂, t₂) —двумерная плотность вероятности.

Часто пользуются иным выражением корреляционной функции, .записанной не для самого случайного процесса X(t), а для центрированной случайной составляющей X(t). Корреляционную функцию в этом случае называют центрированной и определяют из соотношения

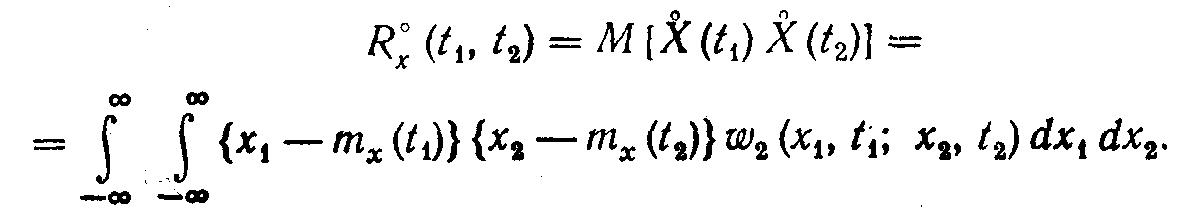(6.2)

Различные случайные процессы в зависимости от того, как изме­няются их статистические характеристики с течением времени, делят на стационарные и нестационарные. Различают стационарность в уз­ком смысле и стационарность в широком смысле.

Стационарным в узком смысле называют случайный процесс X(t), если его n-мерные функции распределения и плотность вероятности при любом п не зависят от положения начала отсчета времени t, т. е.

(6.3)

Это означает, что два процесса, X(t) и X(t+), имеют одинаковые статистические свойства для любого , т. е. статистические характерис­тики стационарного случайного процесса неизменны во времени. Стационарный случайный процесс — это своего рода аналог установивше­гося процесса в детерминированных системах.

Стационарным в широком смысле называют случайный процесс X(t), математическое ожидание которого .постоянно:

(6.4)

а корреляционная функция зависит только от одной переменной — раз­ности аргументов =t₂-t₁:

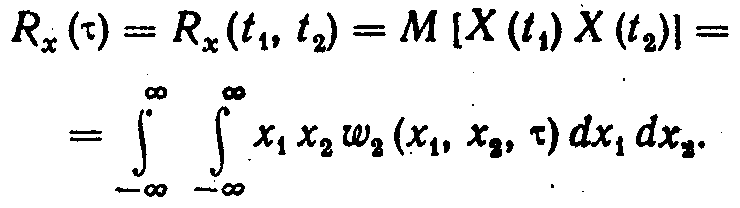(6.5)

Понятие случайного процесса, стационарного в широком смысле,. вводится тогда, когда в качестве статистических характеристик слу­чайного процесса используются только математическое ожидание и корреляционная функция.