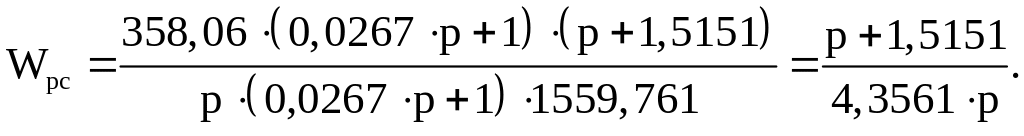- •Реферат
- •Содержание
- •Введение
- •1 Литературный и патентный обзор
- •1.1 Литературный обзор
- •1.2 Патентный обзор
- •2 Характеристика узла выделения ортоксилола
- •2.1 Описание технологического процесса и технологической схемы
- •2.2 Краткая характеристика и режимы работы механического оборудования
- •2.3 Краткая характеристика и режимы работы электрооборудования
- •2.4 Характеристика окружающей среды на установке
- •3 Электрооборудование узла выделения ортоксилола
- •3.1 Расчет мощности и выбор электродвигателей
- •3.2 Обоснование и выбор автоматизированного электропривода узла выделения ортоксилола
- •3.3 Расчет мощности и выбор электрических преобразователей
- •3.4 Обоснование и выбор систем регулирования координат электропривода
- •3.5 Выбор технических средств регулирования координат электропривода
- •4 Разработка системы управления электрооборудованием
- •4.1 Разработка системы управления в статических режимах
- •4.2 Разработка системы управления в динамических режимах
- •5 Расчет статических характеристик системы электропривода
- •5.1 Расчет механических характеристик производственного механизма
- •5.2 Расчет механических характеристик электродвигателя
- •5.3 Анализ статической устойчивости системы электропривода
- •6 Расчет динамических характеристик системы электропривода
- •6.1 Расчет параметров передаточных функций звеньев
- •6.2 Расчет системы автоматического регулирования скорости
- •6.3 Расчет переходных процессов системы регулирования скорости
- •6.4 Анализ переходных процессов
- •Заключение
- •Список использованных источников
5.3 Анализ статической устойчивости системы электропривода
Условие устойчивости системы электропривода
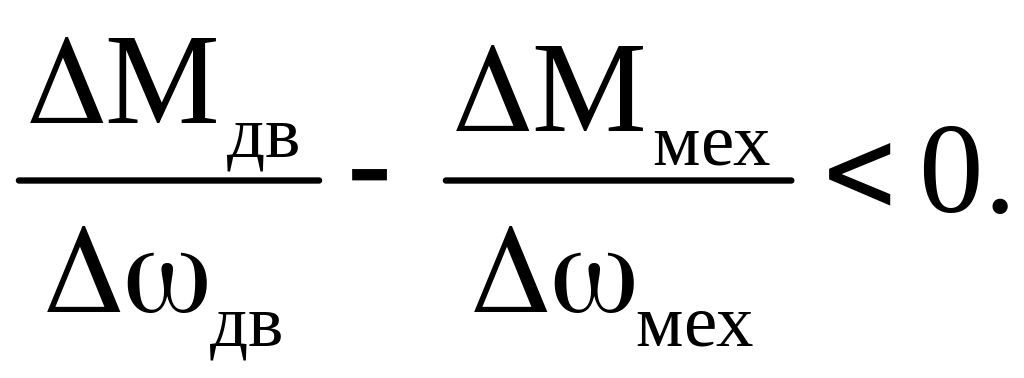 (41)
(41)
Для анализа устойчивости системы электропривода насоса Н-8 изобразим одну из точек пересечения механических характеристик насоса и электродвигателя (рисунок 13).
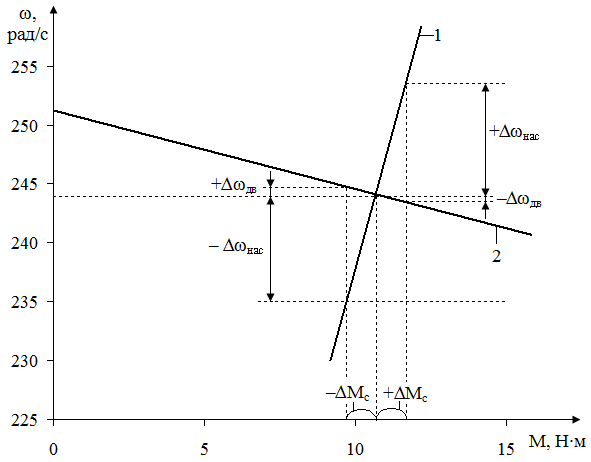
1 – механическая характеристика насоса;
2 – механическая характеристика двигателя
Рисунок 13 – График для анализа статической устойчивости
При изменении момента сопротивления
![]() получаем
получаем
![]() и
и
![]() .
Проверяем условие устойчивости
.
Проверяем условие устойчивости
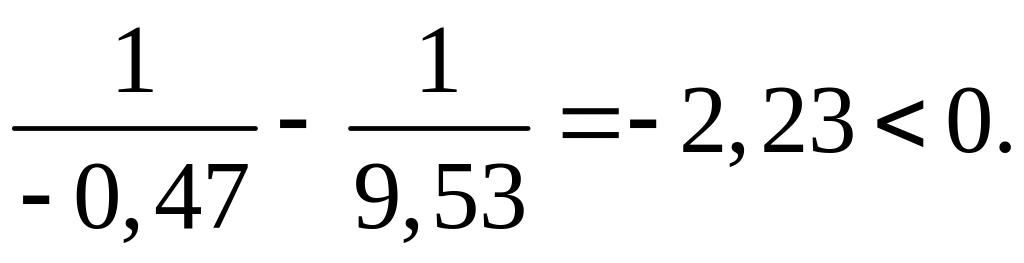
При изменении момента сопротивления
получаем
![]() и
и
![]() .
Проверяем условие устойчивости
.
Проверяем условие устойчивости
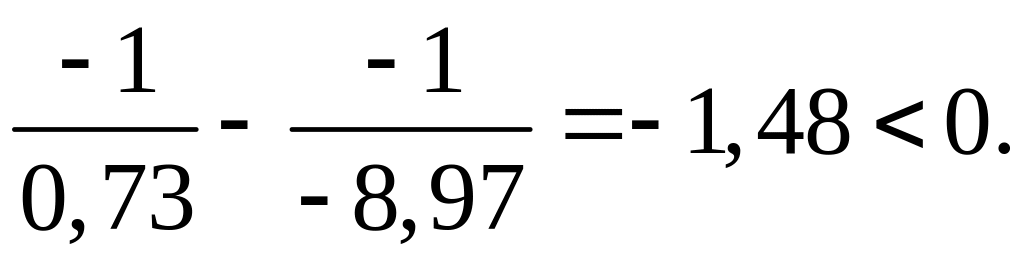
Условия выполняются.
6 Расчет динамических характеристик системы электропривода
6.1 Расчет параметров передаточных функций звеньев
В качестве регулятора скорости асинхронного двигателя используется преобразователь частоты, передаточная функция которого равна коэффициенту передачи по каналу управления частотой
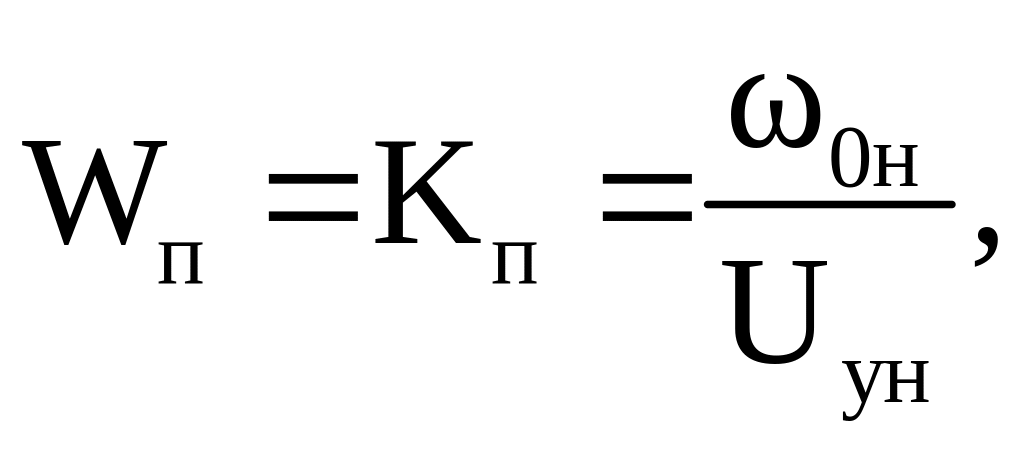 (42)
(42)
где ![]() – номинальная скорость вращения
магнитного поля статора, рад/с;
– номинальная скорость вращения
магнитного поля статора, рад/с;
![]() – управляющий сигнал,
= 16 мА.
– управляющий сигнал,
= 16 мА.
Определяем передаточную функцию для электромеханического преобразователя
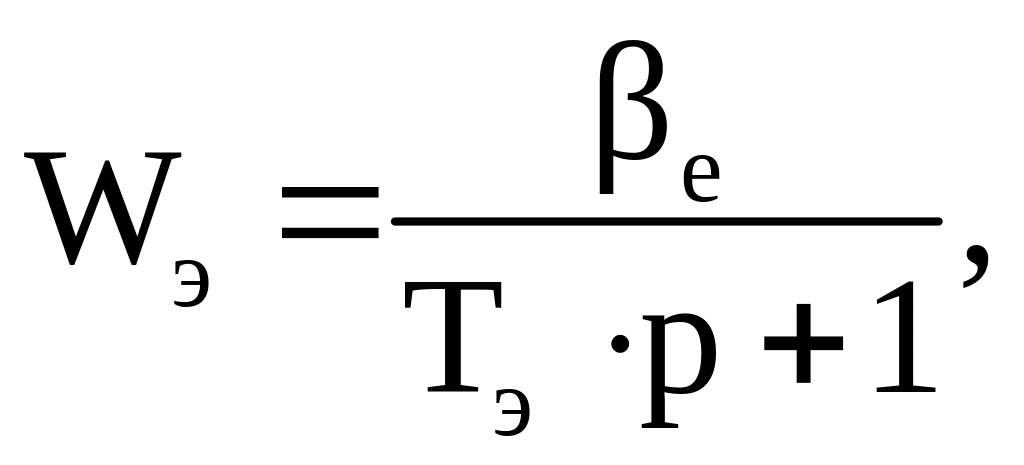 (43)
(43)
где βe – модуль жесткости механической характеристики рабочего участка, Н∙м∙с/рад;
![]() – электромагнитная постоянная времени,
c.
– электромагнитная постоянная времени,
c.
Рассчитываем электромагнитную постоянную времени
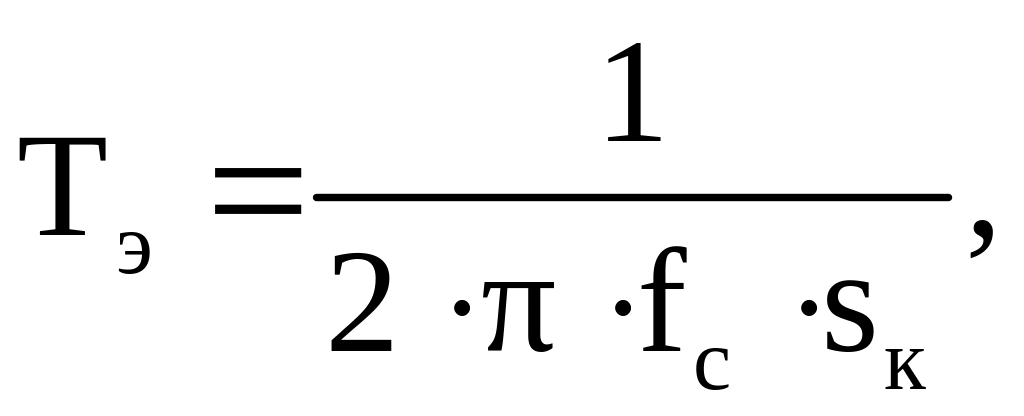 (44)
(44)
где fс – частота сети, fc = 50 Гц.
Определяем критическое скольжение
![]() (45)
(45)
где sн – номинальное скольжение.
Подставив числовые значения в формулы (45), (44), получим
![]()
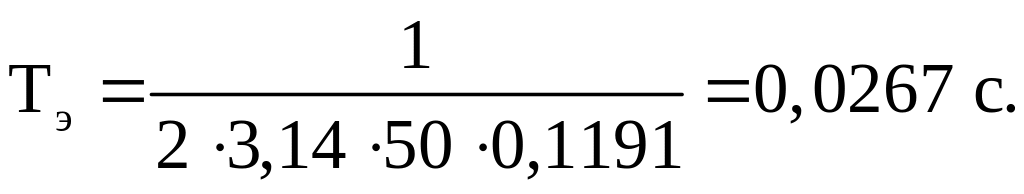
Определяем передаточную функцию для механического преобразователя
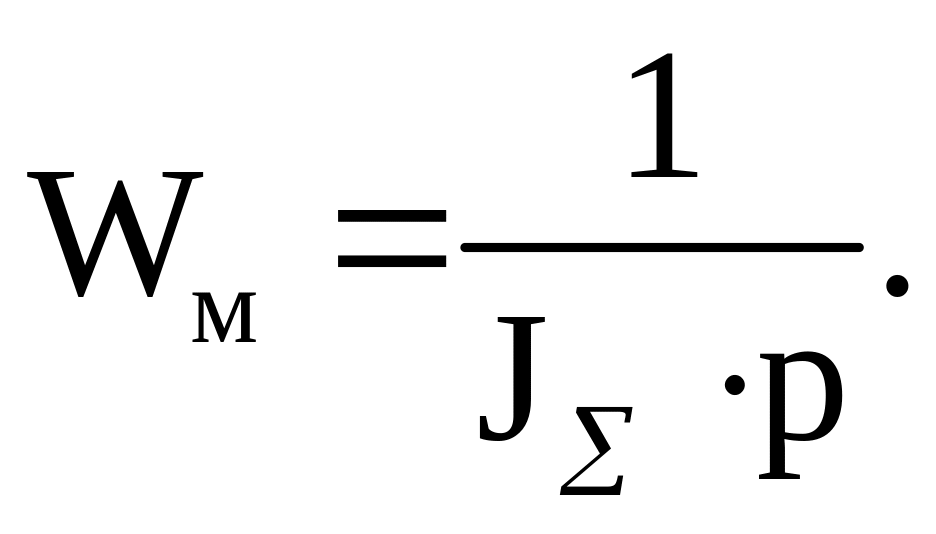 (46)
(46)
Определяем суммарный момент
![]() (47)
(47)
где ![]() – момент инерции центробежного насоса,
кг·м2.
– момент инерции центробежного насоса,
кг·м2.
Определяем момент инерции центробежного насоса
![]() (48)
(48)
Подставив числовые значения в формулы (48), (47), получим
![]()
![]()
Определяем модуль жесткости механической характеристики рабочего участка
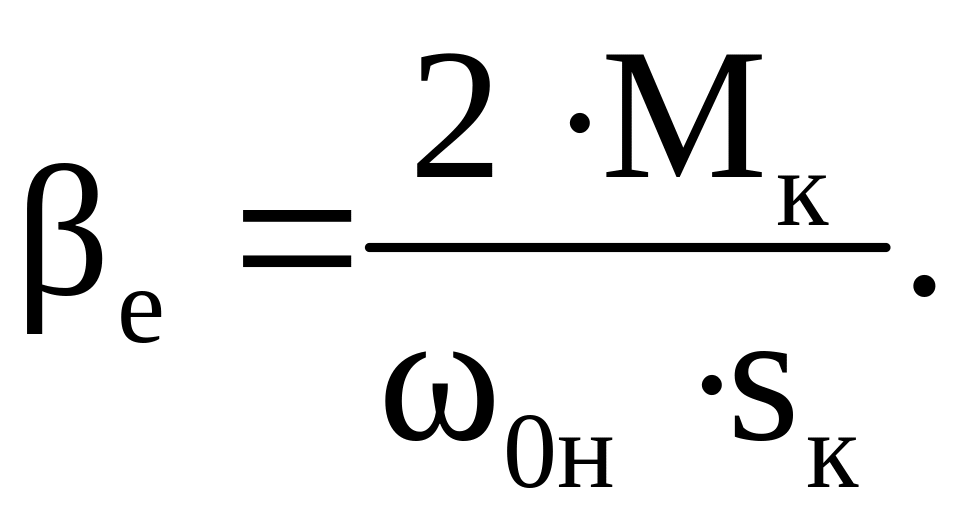 (49)
(49)
Рассчитываем синхронную скорость вращения двигателя
![]() (50)
(50)
где n0н = n1 – синхронная скорость вращения двигателя, об/мин.
Подставив числовые значения в формулу (51), получим
![]()
Рассчитываем коэффициент обратной связи по скорости
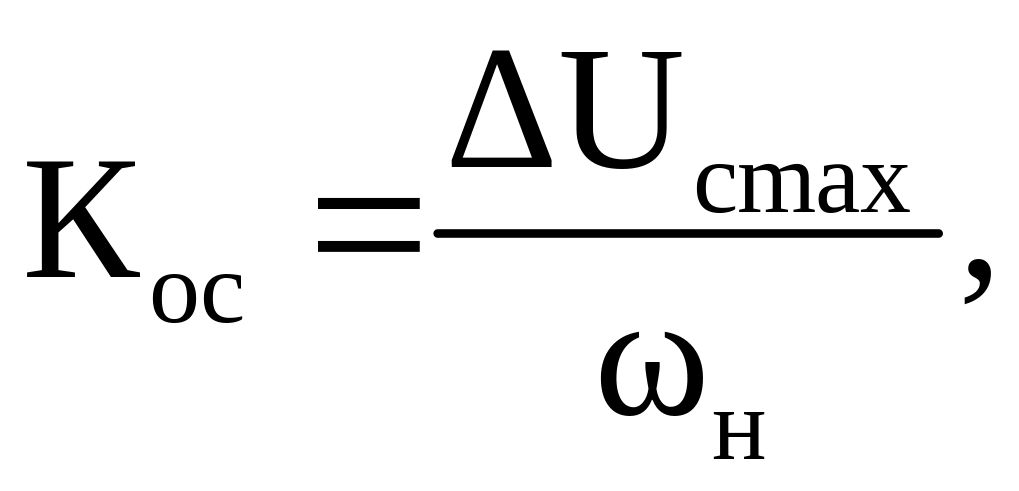 (51)
(51)
где ![]() – сигнал на выходе звена обратной связи,
= 16 мА.
– сигнал на выходе звена обратной связи,
= 16 мА.
Определяем коэффициент связи между скоростью вращения и моментом сопротивления
![]() (52)
(52)
На рисунке 11 по таблице 20 выбираем 2 произвольные точки, в которых Mc1 = 17 Н·м, ω1 = 300 рад/с; Mc2 = 13,4 Н·м, ω2 = 270 рад/с. Определим изменение момента сопротивления и скорости вращения
![]()
![]()
![]()
![]()
Подставив числовые значения в формулы (49), (46), (42), (43), (51), (52), получим
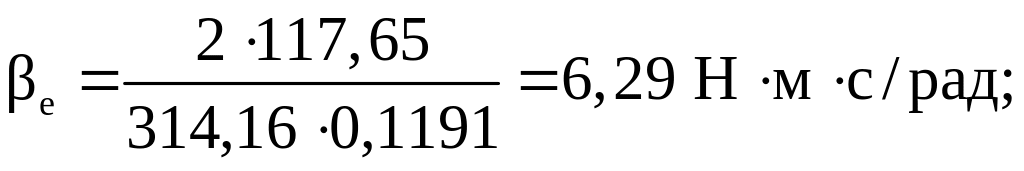
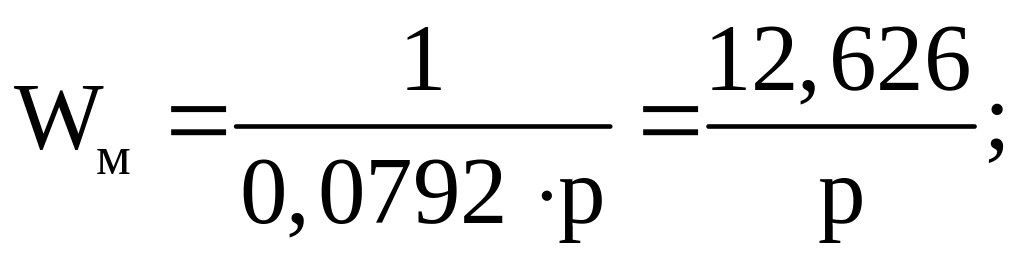
![]()
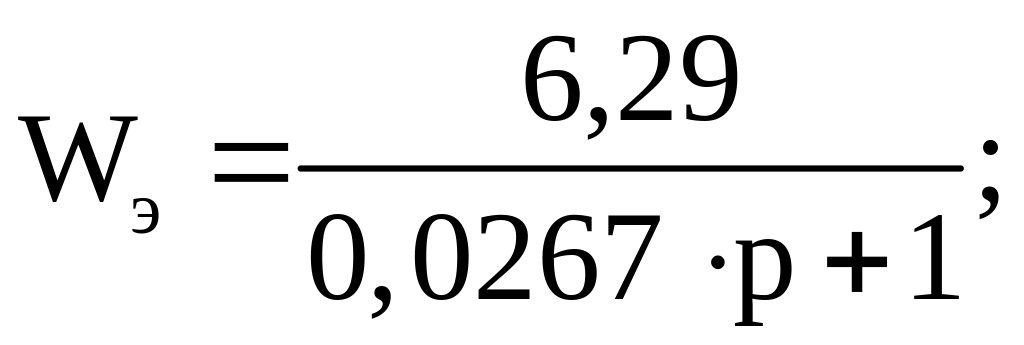
![]()
![]()
6.2 Расчет системы автоматического регулирования скорости
В соответствии со структурной схемой (рисунок 10) передаточная функция объекта регулирования скорости имеет вид
![]() (53)
(53)
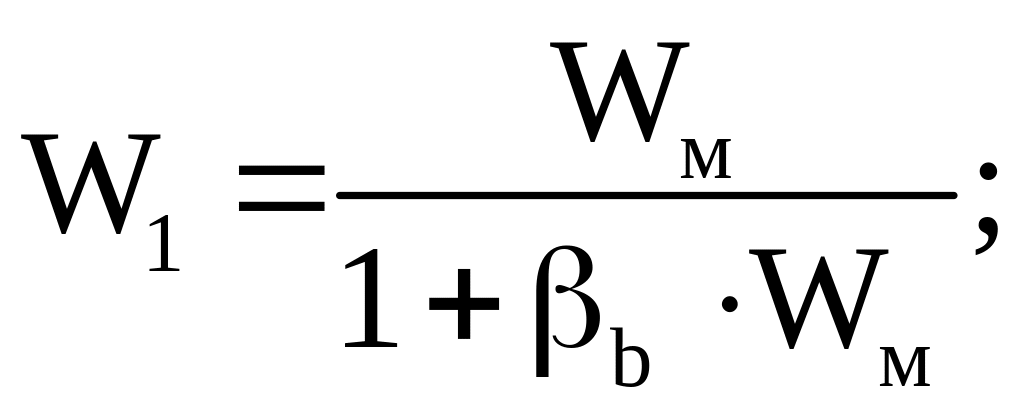 (54)
(54)
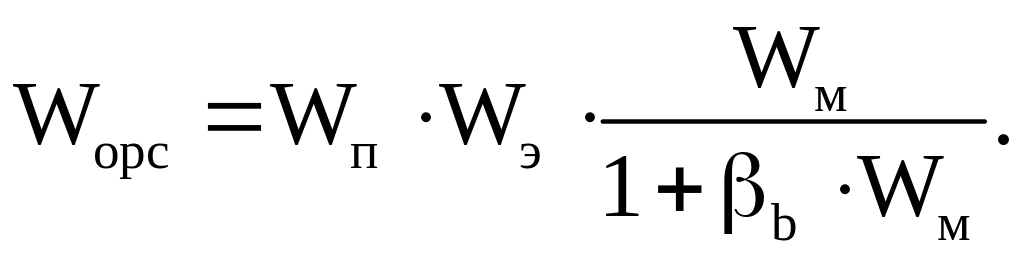 (55)
(55)
Подставив числовые значения в формулу (54), получим
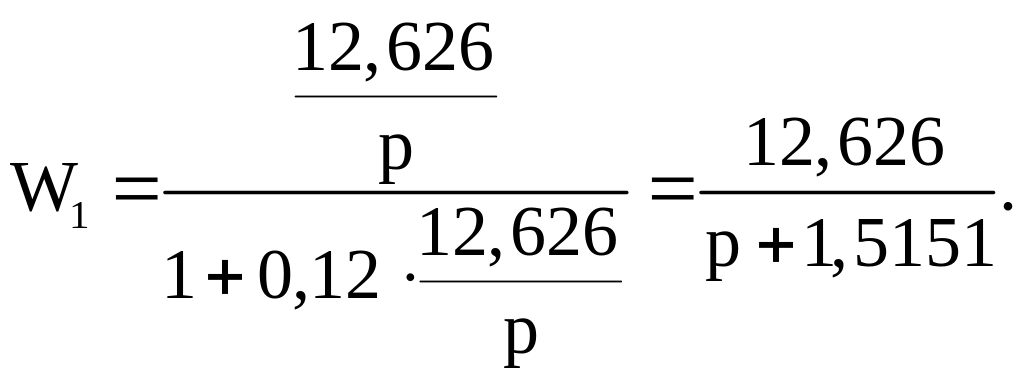
Подставив числовые значения в формулу (55), получим
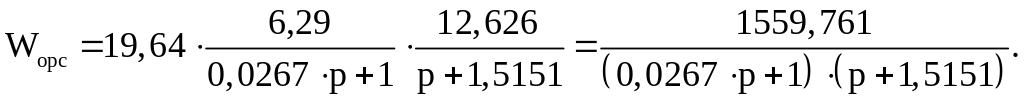
Настройка контура регулирования скорости производится на технический оптимум. Передаточная функция разомкнутого контура регулирования скорости имеет вид
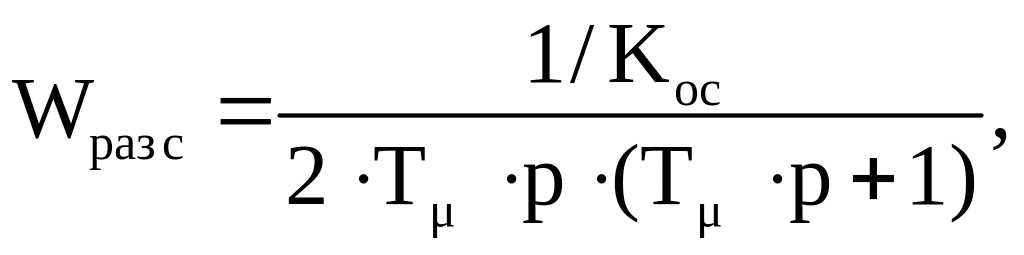 (56)
(56)
где
![]() – сумма малых постоянных времени в
объекте компенсирования скорости,
– сумма малых постоянных времени в
объекте компенсирования скорости,
![]()
Подставив числовые значения в формулу (56), получим
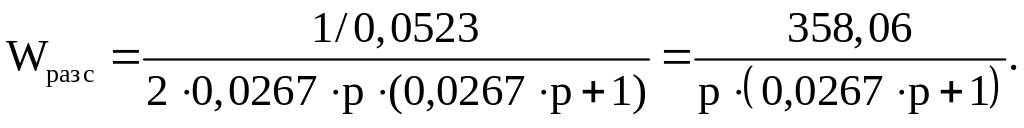
В соответствии с методом последовательной коррекции передаточная функция регулятора скорости примет вид
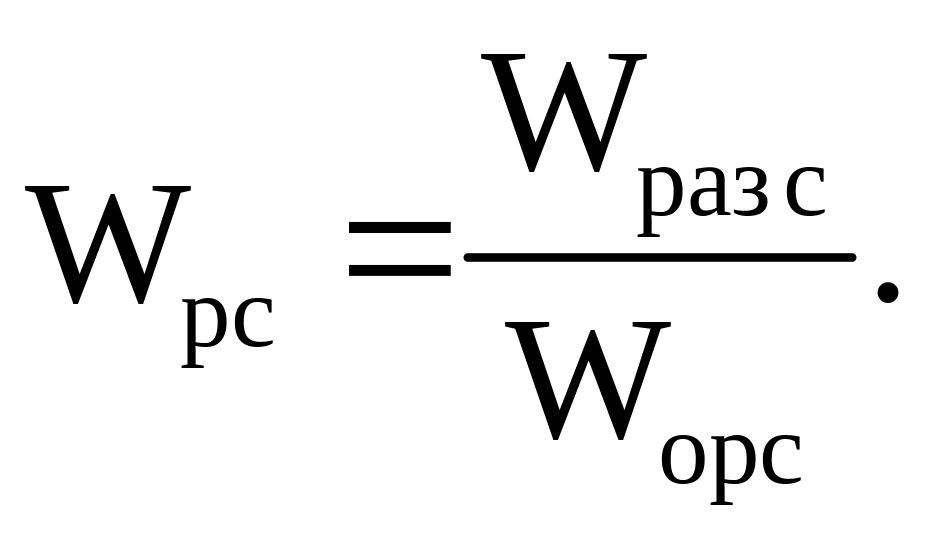 (57)
(57)
Подставив числовые значения в формулу (57), получим