Определение Пусть дана перестановка порядка :

Соответствующей матрицей перестановки является матрица вида: где — вектор длины n, i-й элемент которого равен 1, а остальные равны нулю.

9.Постановка задачи численного решения СЛАУ.Прямые методы решения.Матрица Хаусхольдера, QR-разложение.Метод отражений.Матрица Гивенса и метод вращений.

Численное решение уравнений и их систем состоит в приближённом определении корня или корней уравнения или системы уравнений и применяется в случаях, когда точное значение вычислить невозможно или очень трудоёмко.

или

Численное решение задачи можно проводить как непосредственно (используя одноимённые методы), так и с применением оптимизационных методов, приведя задачу к соответствующему виду.

1. Метод последовательных приближений

2. Метод Гаусса-Зейделя

3. Метод обращения матрицы

4. Триангуляция матрицы

5. Метод Халецкого

6. Метод квадратного корня

Пусть гиперплоскость описывается единичным вектором u, который ортогонален ей, а — скалярное произведение в V, тогда

называется оператором Хаусхолдера.

Матрица Хаусхолдера имеет вид: H=I-2uu*

• Матрица Хаусхолдера является эрмитовой: H=H*

• Матрица Хаусхолдера является унитарной: H*H=I

• Значит она является инволюцией: .

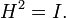• Преобразование 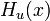отображает точку x в точку x-2(u,x)u

• Преобразование Хаусхолдера имеет одно собственное значение равное (-1), которое отвечает собственному вектору u, все другие собственные значения равны (+1).

• Определитель матрицы Хаусхолдера равен (-1).

QR-разложение матрицы — представление матрицы в виде произведения унитарной (или ортогональной матрицы) и верхнетреугольной матрицы.Матрица A размера nxn с комплексными элементами может быть представлена в виде: A=QR, где Q-— унитарная матрица размера nxn, а R— верхнетреугольная матрица размера nxn.В частном случае, когда матрица A состоит из вещественных чисел, Q является ортогональной матрицей (то есть , где I— единичная матрица).По аналогии, можно определить варианты этого разложения: QL-, RQ-, и LQ-разложения, где L— нижнетреугольная матрица.Если A— квадратная невырожденная матрица, то существует единственное QR-разложение, если наложить дополнительное условие, что элементы на диагонали матрицы R должны быть положительными вещественными числами.

Матрица Гивенса. Поворот Гивенса вектора на плоскости определяется матрицей линейного оператора:

Поэтому для некоторого вектора : . К примеру, для :

10.Постановка задачи численного решения СЛАУ.Метод простой итерации.Методы Якоби, Зейделя и релаксаци.Свойство независимости погрешности от числа итераций.

Численное решение уравнений и их систем состоит в приближённом определении корня или корней уравнения или системы уравнений и применяется в случаях, когда точное значение вычислить невозможно или очень трудоёмко.

или

Численное решение задачи можно проводить как непосредственно (используя одноимённые методы), так и с применением оптимизационных методов, приведя задачу к соответствующему виду.

Метод простых итераций в общем виде. Заменим исходное уравнение на эквивалентное ,и будем строить итерации по правилу . Таким образом метод простой итерации - это одношаговый итерационный процесс. Для того, что бы начать данный процесс, необходимо знать начальное приближение .

Метод якоби

Для того, чтобы построить итеративную процедуру метода Якоби, необходимо провести предварительное преобразование системы уравнений к итерационному виду . Оно может быть осуществлено по одному из следующих правил:

• 

• 

• 

где в принятых обозначениях D означает матрицу, у которой на главной диагонали стоят соответствующие элементы матрицы A, а все остальные нули; тогда как матрицы U и L содержат верхнюю и нижнюю треугольные части A, на главной диагонали которых нули,E— единичная матрица.Тогда процедура нахождения решения имеет вид:

Чтобы пояснить суть метода, перепишем задачу в виде:

Здесь в j-м уравнении мы перенесли в правую часть все члены, содержащие , для i>j. Эта запись может быть представлена:

где в принятых обозначениях D означает матрицу, у которой на главной диагонали стоят соответствующие элементы матрицы A, а все остальные нули; тогда как матрицы U и L содержат верхнюю и нижнюю треугольные части A, на главной диагонали которых нули.

Итерационный процесс в методе Гаусса-Зейделя строится по формуле после выбора соответствующего начального приближения .

Метод Гаусса-Зейделя можно рассматривать как модификацию метода Якоби. Основная идея модификации состоит в том, что новые значения используются здесь сразу же по мере получения, в то время как в методе Якоби они не используются до следующей итерации:

где . Таким образом, i-тая компонента -го приближения вычисляется по формуле:

Метод релаксации - итерационный метод решения систем линейных алгебраических уравнений.

Система линейных уравнений

13.Приближенное вычисление производных. Построение конечно разностных формул численного дифференциирования и оценка их точности. Метод неопределённых коэфицентов.

Пусть K_n - система узловых точек a = x₀ < x₁ <…< x_n = b. Функция S_k(x) называется сплайн-функцией S_k(x) степени k≥0 на K_n, если

а) S_k(x) є C^k-1([a, b]) б) S_k(x) - многочлен степени не большей k; Сплайн-функция Ŝ_k(x) є S_k(K_n) называется интерполирующей сплайн-функцией, если Ŝ_k(x_j) = f(x_j) для j = 0,1,…,n В приложениях часто бывает достаточно выбрать k=3 и применить т. н. кубическую интерполяцию.

Т. к. s(x) на каждом частичном интервале есть многочлен третьей степени, то для x є [x_j-1 ,x_j]

Здесь s²_j, c_j1, c_j0 неизвестны для j = 1, 2, …, nПоследние исключаются в силу требования s(x_j) = y_j: Дифференцируя эту функцию и учитывая, что s'(x) на всем интервале и, следовательно, в частности, в узлах должна быть непрерывна, окончательно получаем систему уравнений:

приводится к виду где ,

Находятся невязки :

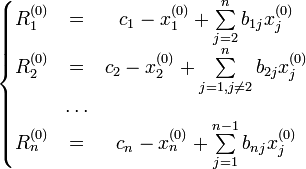
Выбирается начальное приближение . На каждом шаге необходимо обратить в ноль максимальную невязку: . Условие остановки: . Ответ находится по формуле: .

14.Понятие о численном решении задачи Коши для систем ОДУ. Понятие устойчивости, аппроксимаци и сходимости дискретных систем, теорема В.С. Рябенького-П.Лакса.Методы Эйлера и Рунге-Кутта.

Постановка задачи Коши

Метод Рунге-Кутта относится к методам численного решения обычных дифференциальный уравнений первого порядка. Этот численный метод является одним из точных методов численного решения ОДУ и систем ОДУ, и не очень сложных в реализации, поэтому этот медот получил широкое распространение. Задача Коши для ОДУ первого порядка ставится следующим образом: dy/dx=F(x,y) .Как и для любых других чесленных методов решения дифференциальных уравнений, для решения этого уравнения требуется задать начальные условия: x0, y0. Математическое решение задачи Решением поставленной задачи будет ряд точек на плоскости (x,y). Обозначим шаг вычислений как h. Вектор точек по оси x обозначим x[i], i=0...N, при этом значения этого вектора будут определяться следующим образом: x[i]=x[0]+h*i. Вектор точек по оси y обозначим как y[i]. Тогда значения ветора y будут определяться следующим образом:

y[i+1]=y[i]+delta; delta=(K1+2*K2+2*K3+K4)/6; K1=h*F(x[i],y[i]); K2=h*F(x[i]+h/2,y[i]+K1/2); K3=h*F(x[i]+h/2,y[i]+K2/2); K4=h*F(x[i]+h,y[i]+K3);

Таким образом будет получено численное решение исходного дифференциального уравнения на интервале [a,b] с заданными начальными условиями и шагом. Аппроксимация – процесс подбора эмпирической функции φ(х) для установления из опыта функциональной зависимости y= φ(х). Основная задача аппроксимации – построение приближенной (аппроксимирующей) функции наиболее близко проходящей около данных точек или около данной непрерывной функции.