1.Работа с массивами NumPy

Создание массивов

Есть много способов для того, чтобы создать массив. Например, вы можете создать массив из обычных списков или кортежей Python, используя функцию array(): >>> from numpy import * >>> a = array( [2,3,4] ) >>> a array([2, 3, 4]) >>> type(a) < type 'numpy.ndarray'>

Базовые операцииАрифметические операции над массивами выполняются поэлементно. Создается новый массив, который заполняется результатами действия оператора.В отличие от матричного подхода, оператор произведения * в массивах NumPy работает также поэлементно. Матричное произведение может быть осуществлено либо функцией dot().Некоторые операции делаются «на месте», без создания нового массива. При работе с массивами разных типов, тип результирующего массива соответствует более общему или более точному типу. Многие унарные операции, такие как вычисление суммы всех элементов массива, представлены в виде методов класса ndarray.

Универсальные функцииNumPy обеспечивает работу с известными математическими функциями sin, cos, exp и так далее. Но в NumPy эти функции называются универсальными (ufunc). Причина присвоения такого имени кроется в том, что в NumPy эти функции работают с массивами также поэлементно, и на выходе получается массив значений.

Индексы, срезы, итерацииОдномерные массивы осуществляют операции индексирования, срезов и итераций очень схожим образом с обычными списками и другими последовательностями Python.У многомерных массивов на каждую ось приходится один индекс. Индексы передаются в виде последовательности чисел, разделенных запятыми.

2.Постановка задачи интерполяции.Интерполяционные многочлены Лагранжа и Ньютона.Теорема об остаточном члене интерполяции.Оценка погрешности многочленной интерполяции и её обусловленность.

Задача интерполяции функции, интерполяционные полиномы

Пусть на отрезке [a,b] задана функция ƒ(x). Задача интерполяции (или интерполирования) состоит в построении функции g(x), совпадающей с заданной ƒ(x) в некотором наборе точек {x₁,x₂,...,x_n+1} из отрезка [a,b] (эти точки называются узлами интерполяции), т.е. должны выполняться условия:g(x_k)=y_k, k=1,2,...,n+1,где y_k - известные значения функции ƒ(x) в точках x_k. Функция g(x) называется интерполянтом функции ƒ(x).

Интерполяционный полином в форме Лагранжа

Интерполяционный полином в форме Ньютона.

N_n(t) = f(t₁) + f(t₁, t₂)(t - t₁) + ... + f(t₁, ..., t_{n + 1})(t - t₁) ... (t - t_n).

Теорема об остаточном члене интерполяции

Введем понятие остаточного члена интерполяции для оценки погрешности

Теорема. Пусть функция f(t) имеет на отрезке [a, b] — N + 1 ограниченную производную. Тогда где

3.Постановка задачи интерполяции.Кусочно многочленная глобальная интерполяция.Естественный сплайн, построение кубического сплайна Шонберга.Локальная интерполяция, B-сплайны.

Задача интерполяции функции, интерполяционные полиномы

Пусть на отрезке [a,b] задана функция ƒ(x). Задача интерполяции (или интерполирования) состоит в построении функции g(x), совпадающей с заданной ƒ(x) в некотором наборе точек {x₁,x₂,...,x_n+1} из отрезка [a,b] (эти точки называются узлами интерполяции), т.е. должны выполняться условия:g(x_k)=y_k, k=1,2,...,n+1,где y_k - известные значения функции ƒ(x) в точках x_k. Функция g(x) называется интерполянтом функции ƒ(x).

Кусочно - многочленная глобальная интерполяция (сплайны).Определение. Пусть на отрезке [a, b] задана система узловых точек Сплайном S_m(t) называется определенная на [a, b] функция, имеющая l непрерывных производных и являющаяся на каждом интервале (t_{n - 1}, t_n) многочленом степени m.

B - сплайном, или базисным сплайном степени N - 1 дефекта 1 относительно узлов называется функция

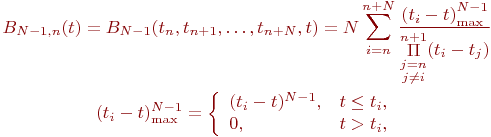
Пусть т.е. рассматривается случай равномерной сетки.

естественный сплайн кусочно - квадратичная функция с первой непрерывной производной .

4.Приближение функции.Метод наименьших квадратов и его приминение к обработке эмпирических данных. Решение переопределённых систем линейных алгебраческих уравнений.

ПРИБЛИЖЕНИЕ ФУНКЦИЙ

замена по определенному правилу функции f(t).близкой к ней в том или ином смысле функцией j(t). из заранее фиксированного множества M(приближающего множества). Предполагается, что функция f определена на том множестве Qm-мерного евклидова пространства (в частности, действительной оси), на к-ром осуществляется приближение, она может быть задана явно через элементарные функции или быть решением нек-рого уравнения. Если о функции f(t) располагают неполной информацией, то тогда речь идет, по существу, о приближении задаваемого этой информацией целого класса фу нкций.

Метод наименьших квадратов -- один из методов теории ошибок для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. Идея МНК основана на том, чтобы минимизировать сумму квадратов отклонений расчетных значений от эмпирических, т.е. нужно оценить параметры о функции f(a,x) таким образом, чтобы ошибки е_i= у_i-f(а,х), точнее - их квадраты, по совокупности были минимальными.Переопределённые слау это те слау в которых число уравнений больше числа неизвестных.Чтобы решить переопределённкю СЛАУ нужно вместо точного решения ситемы уравнений организовать поиск такого вектора y, который будет наилучшим образом удовлетворять всем уравнениям, т.е. минимизировать их невязку(расхождение между вектором A*x и вектором B в правой части). Поскольку невязка A*x-B является векторной велииной то исходя из практических соображений минимизации надо подвергать её норму(т.е. скаляр).

5.Постановка задачи численного интегрирования.Квадратурные формы интерполяционного типа.(Формулы Ньютона-Котеса): формулы прямоугольников, трапеций и Симпсона.Оценка их точности.

Суть численного интегрирования заключается в том, что подынтегральную функцию f(x) заменяют другой приближенной функцией, так, чтобы, во-первых, она была близка к f(x) и, во вторых, интеграл от нее легко вычислялся. Например, можно заменить подынтегральную функцию интерполяционным многочленом.Простейшую квадратурную формулу (формулу численного интегрирования) можно получить следующим образом. Пусть необходимо вычислить интеграл

Положим, что f(t)на рассматриваемом отрезке [a, b]не изменяется ( ). Тогда Если

то получим формулу прямоугольников с центральной точкой

Если предположить, что функция f(t)на отрезке интегрирования [a, b]достаточно близка к линейной, то можно заменить приближенное значение интеграла iплощадью трапеции с высотой (b - a)и основаниями f(a)и f(b). Тогда получается формула трапеций

В общем случае квадратурные формулы получаются при помощи интегрирования интерполяционного многочлена, аппроксимирующего подынтегральную функцию. Семейство квадратурных формул, получающихся таким образом, называется формулами интерполяционного типа(формулы Ньютона - Котеса) .Формула трапеций. На отрезке [t_k, t_{k + 1}]проводим замену подынтегральной функции интерполяционным полиномом первой степени:

после чего, выполнив интегрирование по элементарному отрезку, получим приближенное значение интеграла на [t_k, t_{k + 1}]:

После суммирования интегралов по всем элементарным отрезкам [t_k, t_{k + 1}]получаем формулу трапеций для отрезка [a, b]:

Формула Симпсона. Заменим подынтегральную функцию f(t)на отрезке [t_{k - 1}, t_k]интерполяционным полиномом (в форме Лагранжа) второй степени. Для простоты положим для всех k— сетка на отрезке интегрирования равномерная. Тогда

6.Постановка задачи численного решения систем нелинейных уравнений.Основные этапы.Методы простой итерации и Ньютона: идея метода,алгоритм и критерий его применимости.Скорость сходимости метода Ньютона.

О бщий вид решения системы нелинейных арифметических уравнений имеет вид:

F1(X1,…,Xn)=0

…

Fn(X1,…,Xn)=0

, где Fi– функция nпеременных.

Решением СНАУ является вектор X=(X1,…,Xn),при подстановке компонент которого в систему каждое её уравнение обращается в верное равенство.

Метод простых итераций в общем виде. Заменим исходное уравнение на эквивалентное ,и будем строить итерации по правилу . Таким образом метод простой итерации - это одношаговый итерационный процесс. Для того, что бы начать данный процесс, необходимо знать начальное приближение .

Меод Ньютона(алгоритм)

1. Задается начальное приближение .

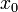2. Пока не выполнено условие остановки, в качестве которого можно взять 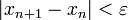или (то есть погрешность в нужных пределах), вычисляют новое приближение: .

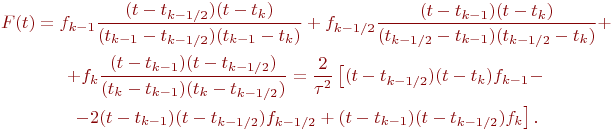
После вычисления интеграла от полинома получим приближенное значение интеграла по элементарному отрезку

Суммируя по всем элементарным отрезкам [t_{k - 1}, t_k], получим

где

7.Нормы векторов и матриц,обусловленность системы и матрицы системы.Постановка задачи численного решения СЛАУ.Прямой метод гауса и его модификация.