4. Нейронные сети

Нейронные сети – это вычислительные структуры, моделирующие простейшие биологические процессы, подобные процессам, протекающим в нашем мозге. Сам термин «нейронная сеть» впервые появился в 40-е годы в среде ученых, изучающих принципы организации и поведения биологических нейронных систем. Нейронные сети строятся на элементах, которые называются искусственными нейронами или просто нейронами по аналогии с биологическим прототипом.

Нейронные сети, благодаря заложенным в них способностям к адаптации и обучению, оказываются хорошо приспособленными для решения следующих задач.

1. Классификация образов, представленных векторами признаков. К известным реализациям относятся системы распознавания букв, речи, особенностей кардиограмм, клеток крови.

2. Предсказание / прогноз. Пусть имеется вектор отсчетов некоторого сигнала в моменты времени . Требуется, на основании имеющейся истории изменения сигнала, найти оценку для его значения в ещё не наступивший момент времени . Возможность прогнозирования имеет большое значение в науке, в технике, в бизнесе.

3. Оптимизация. Большое число задач в технике, медицине, экономике сводится к поиску оптимальных решений, решений, которые при соблюдении определенных условий обращают в минимум или максимум некоторую целевую функцию. При наличии очень большого числа переменных, влияющих на принятие решения, эта задача становится трудно выполнимой.

4. Управление. Многие задачи управления сводятся к поиску такого управляющего воздействия, которое заставит выходную величину изменяться по траектории, как можно близкой к заданной.

5. Ассоциативная память или память, адресуемая по содержимому. В классических вычислительных машинах, исповедующих принципы фон Неймана, обращение к памяти доступно только по адресу, никак не связанному с содержанием информации, находящейся в памяти. Ассоциативная память, которая может быть реализована нейронными сетями, доступна по указанию заданного содержания. Ассоциативная память оказывается очень важной при создании мультимедийных информационных баз данных.

Нервная система и мозг состоят из биологических нейронов, связанных друг с другом нервными волокнами. Все процессы передачи возбуждений от кожи, ушей, глаз, языка, все процессы мышления и управления действиям, все это реализуется как процессы передачи электрических импульсов между нейронами.

Нейрон – это особая биологическая клетка, которая обрабатывает информацию. Как и всякая другая клетка, нейрон состоит из тела (сома) с ядром и отростками нервных волокон двух типов: нескольких дендритов, по которым поступают импульсы возбуждения, и единственного аксона, который передает сигнал другим нейронам.

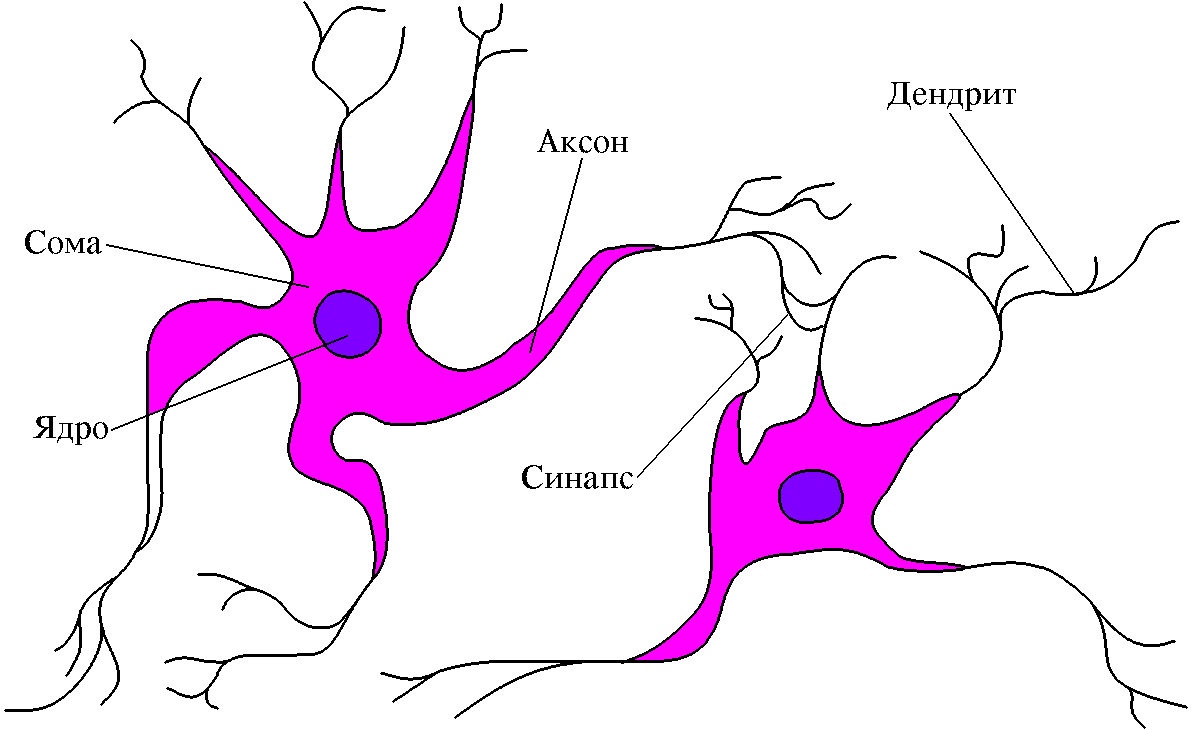
Аксон разделяется на ряд волокон, по которым сигнал может передаваться сразу нескольким нейронам. На концах волокон находятся специальные образования – синапсы, которые изменяют интенсивность сигнала. Усиление или ослабление сигнала может изменяться во времени и в зависимости от интенсивности сигналов, походивших через синапс ранее. Эта зависимость от предыстории действует как память и создает условия для обучения и самообучения нейронов.

Математическая модель нейрона, то есть искусственный нейрон или нейроподобный элемент, строится следующим образом.

В состав нейрона входят умножители (синапсы), сумматор сигналов от других нейронов, умноженных на веса синапсов , и нелинейного элемента , реализующего зависимость выходного сигнала нейрона от единственного аргумента – выхода сумматора . Функция называется функцией активации нейрона. Кроме того, на сумматор подается независимое смещение .

М атематическая модель нейрона описывается двумя формулами:

Таким образом, нейрон преобразует входной векторный сигнал в скалярный сигнал. Синоптические связи с положительными весами считаются возбуждающими, связи с отрицательными весами – тормозящими.

В качестве функций активации чаще других используются:

пороговая функция ,

- сигмоидальная функция (сигмоид) с замечательным свойством

Искусственная нейронная сеть – это набор нейронов, соединенных между собой. Активационные функции всех нейронов выбраны заранее и, как правило, одинаковы для всех нейронов. Синоптические веса являются параметрами сети и могут изменяться в процессе настройки и обучения сети. Некоторые входы нейронов являются входными для сети и получают сигналы от измерительной аппаратуры. Некоторые выходы нейронов образуют выходы сети. Остальные нейроны являются промежуточными. Хотя именно в них и выполняется вся работа.

Важно помнить, что нейронная сеть может быть реализована на больших интегральных схемах, но все же чаще нейронная сеть – это программа, реализуемая компьютером.

Подавая что-то на вход сети, мы получаем набор чисел на выходе сети. Таким образом, работа сети заключается в преобразовании входного вектора в выходной вектор . Компонентами этих векторов являются значения сигналов на входах и выходах сети. Конкретный вид преобразования определяется набором синоптических весов.

Задача распознавания рукописных букв:

Дано: растровое черно-белое изображение буквы размером пикселей.

Определить: какую букву (из 33 букв русского алфавита) отображает эта картинка.

В терминах нейронных технологий эта же задача формулируется следующим образом:

Дано: входной вектор из 900 двоичных символов .

О пределить: построить нейронную сеть с 900 входами и 33 выходами, которые помечены буквами. Если на входе сети – изображение буквы «А», о максимальное значение выходного сигнала достигается на выходе «А». Аналогично сеть должна работать для всех 33 букв.

По своей архитектуре можно выделить следующие разновидности сетей.

В полносвязной сети каждый нейрон передает сигнал всем другим нейронам сети. Все входные сигналы подаются на все нейроны. Некоторые нейроны образуют выходные сигналы.

В многослойных сетях нейроны объединяют в слои. Слой содержит нейроны с едиными входными сигналами. Число нейронов в каждом слое может быть любым и никак не связано с числом нейронов в соседних слоях. Слой входных нейронов считается нулевым слоем. Кроме входного и выходного слоев имеются промежуточные или скрытые слои.

На множестве многослойных сетей выделяются сети прямого распространения (без обратных связей) и сети с обратными связями. Для них возникает проблема динамической устойчивости, даже если сеть построена в виде программы.

Обучить нейронную сеть – это значит сообщить ей, чего мы от неё хотим. Процесс обучения выглядит следующим образом.

И меется некоторая база данных, содержащая примеры, например, наборы рукописных изображений букв. Предъявляя изображение некоторой буквы на вход сети, мы получаем ответ, не обязательно верный, но нам известен и верный ответ. Обычно в качестве желаемого выхода в задачах классификации берут вектор с 33 компонентами, где стоит на месте, соответствующем желаемому выходу. Далее вычисляется разность между векторами желаемого и действительного ответов сети, например . Алгоритм обучения сети – это просто набор формул, позволяющий вычислять поправки для синоптических весов сети.

Оказывается, что после многочисленных предъявлений сети примеров из имеющейся базы данных веса сети стабилизируются, и сеть начинает давать правильные ответы на почти все примеры. В этом случае говорят, что сеть обучена, натренирована. В процессе обучения функция ошибок, например сумма квадратов элементов вектора ошибок, постепенно уменьшается. Когда она достигает приемлемого уровня, обучение прекращают.

Вся информация, которую сеть имеет о постановке задачи, содержится в примерах. Поэтому качество работы сети напрямую зависит от количества и разнообразия примеров.

Один из самых распространенных алгоритмов обучения – это алгоритм обратного распространения ошибки, который широко используется для обучения многослойных нейронных сетей с последовательными связями. Нейроны имеет сигмоидальную функцию активации. Функция ошибок – сумма квадратов разностей желаемого и действительного вектора ошибок. Коррекция весов нейронов проводится в порядке, обратном ходу распространения сигналов между слоями. Алгоритм действует циклически, его циклы принято называть эпохами:

Шаг 1. Весам сети присваиваются небольшие начальные значения.

Шаг 2. Выбирается очередная обучающая пара . Вектор подается на вход сети.

Шаг 3. Определяется выход сети .

Шаг 4. Вычисляется разность между требуемым значением и реальным выходом сети и средний квадрат ошибок ..

Шаг 5. Веса сети корректирую так, чтобы уменьшить средний квадрат ошибок, причем вначале корректируют веса выходного слоя, затем предыдущего и так далее.

Шаг 6. Шаги со 2-го по 5-й повторяют до тех пор, пока ошибка не достигнет приемлемой величины.

В программе MathLab имеются богатые средства для проектирования и обучения нейронных сетей. Кроме того, имеются и специализированные программы построения нейронных сетей.

197