7.2.4 Описание классов априорного алфавита объектов на языке априорного словаря признаков.
Априорное описание классов - наиболее трудоемкая из задач в процессе создания системы распознавания, требующая глубокого изучения свойств объектов распознавания, но она является и наиболее творческой задачей.
В рамках решения этой проблемы необходимо каждому классу поставить в соответствие:
- числовые параметры детерминированных и вероятностных признаков,
- значения логических признаков,
- предложения, составленные из структурных признаков.
Значения этих параметров описаний находят путем:
- проведения специально поставленных экспериментальных работ или экспериментальных наблюдений;
- обработки экспериментальных данных;
- математических расчетов;
- математического моделирования;
- извлечения данных из литературных источников.
Теперь перейдем к формализации описания классов на языке признаков.
В
геометрической интерпретации множество
признаков детерминированных
рассматривается как пространство
признаков размерности
,
в котором каждый признак
может принимать значения различные
значения
.
Тогда каждому объекту распознавания
будет соответствовать определенный
вектор (или набор) признаков
.
Пусть
далее проведена классификация объектов
распознавания на М классов
.
Для каждого класса
признаки
могут принимать значения
из некоторых интервалов. Поэтому все
пространство признаков разбивается на
М непересекающихся областей
.
Если для какого-то объекта распознавания
вектор признаков
,
то это означает, что объект принадлежит
классу
,
то есть
.
В
алгебраической интерпретации необходимо
построить некоторые разделяющие функции
числом, равным числу классов объектов.
Разделяющие функции должны обладать
следующим свойством. Если объект
,
имеющий признаки
,
принадлежит классу
,
, то функция
принимает значение
,
большее, чем значение любой другой
функции
.
В такой интерпретации разделяющие
функции являются полным описанием
классов на языке признаков.
Границы
между областями
и
в пространстве признаков
описываются гиперповерхностями
,
которые называются решающими границами.
Пример.
В
метро объявляют, что нельзя провозить
предметы, сумма габаритов которых
превышает 2 м. Этим предполагается
существование двух классов предметов
и
.
В плоском случае эти объекты характеризуются
двумя признаками: длина
и ширина
.
Если
для некоторого чемодана окажется, что
,
то он принадлежит классу
и его можно провести бесплатно, если же
,
то он принадлежит классу
,
и за него придется заплатить.
В качестве решающих функций можно принять следующие функции:
Р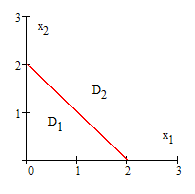
ешающая
граница в двухмерном пространстве
признаков определяется выражением
.
На
рисунке показано соответствующее
разбиение пространства признаков на
две непересекающиеся области
,
в которых лежат те значения вектора
признаков, при получении которых объекты
можно отнести к классам
и
.
В пространствах признаков более высокого порядка все эти соотношения выглядят гораздо сложнее, во всяком случае, менее наглядно.
Несколько сложнее обстоит дело с описанием классов на языке вероятностных признаков. Значения вероятностных признаков случайным образом распределены по всему пространству признаков. В этом случае в качестве описания классов объектов приходится принимать:
-
условные плотности распределения
признаков
при условии, что объект распознавания
принадлежит классу
:
,
-
априорные вероятности
того, что некоторый объект
,
случайным образом выбранный из всей
совокупности объектов, принадлежит
классу
.
Этих данных достаточно, для того чтобы после получения измерительной информации о признаках объекта принять однозначное решение о принадлежности тому или иному классу. Здесь, однако, приходится считаться с неизбежностью определенных вероятностей появления ошибок первого и второго рода.