6.5.2 Характеристики плана контроля

Важнейшими характеристиками плана статистического контроля CSP-1 являются следующие.

1. Средняя продолжительность фазы 100% - го контроля.

Продолжительность фазы 100% - го (сплошного) контроля - это случайная величина, равная числу изделий, проконтролированных в этой фазе, включая последние i годных изделий, её завершающих. Возможное наименьшее значение так определенной продолжительности фазы сплошного контроля равно, очевидно, релаксационному числу i, и появляется с вероятностью . Возможное наибольшее значение равно бесконечности, но имеет место с вероятностью, равной нулю.

Определение распределения для возможных значений продолжительности фазы сплошного контроля представляет собой достаточно сложную комбинаторную задачу. В технической литературе приводится выражение для математического ожидания случайной величины , которое называется средней продолжительностью фазы сплошного контроля:

На рис. 11 приведены построенные по этому уравнению графики зависимости средней продолжительности фазы сплошного контроля (в логарифмических единицах) от релаксационного числа при нескольких постоянных уровнях дефектности технологического процесса и от уровня дефектности при нескольких фиксированных значениях релаксационного числа.

И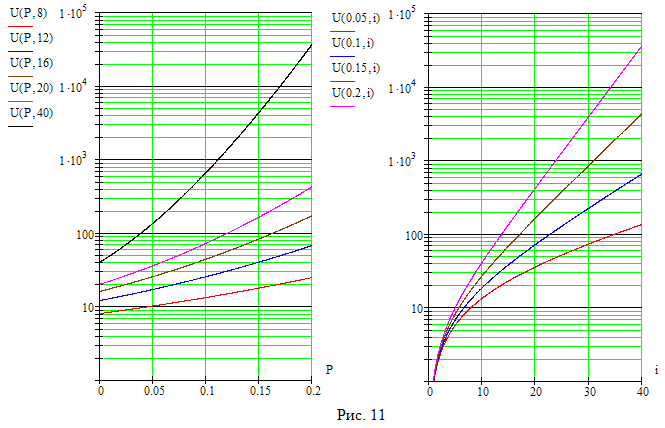 з приведенных графиков видно, что средняя продолжительность фазы сплошного контроля увеличивается как с ростом уровня дефектности технологического процесса, так и с увеличением релаксационного числа, и может достигать очень больших значений.

2. Средняя продолжительность фазы выборочного контроля.

Продолжительность фазы выборочного контроля является также случайной величиной , зависящей от уровня дефектности контролируемого технологического процесса и интервала между выборками. Её математическое ожидание

определяет значение средней продолжительности фазы выборочного контроля.

3. Средняя продолжительность цикла.

Цикл состоит из фазы сплошного контроля, завершающегося обнаружением серии из i следующих друг за другом годных изделий и фазы выборочного контроля. Продолжительность цикла, измеренная в количестве изделий, является случайной величиной, которая образуется как сумма продолжительности фазы сплошного и фазы выборочного контроля . Средняя продолжительность цикла составляет:

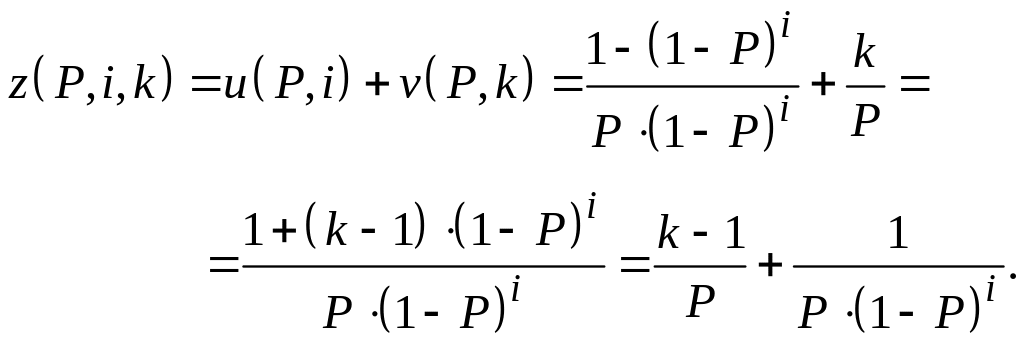
На рис. 12 и 13 показаны графики, иллюстрирующие ход изменения средней продолжительности цикла c увеличением уровня дефектности технологического процесса при k=4 и при различных значениях релаксационного числа i, и графики, построенные при i=16 и различных значениях k.

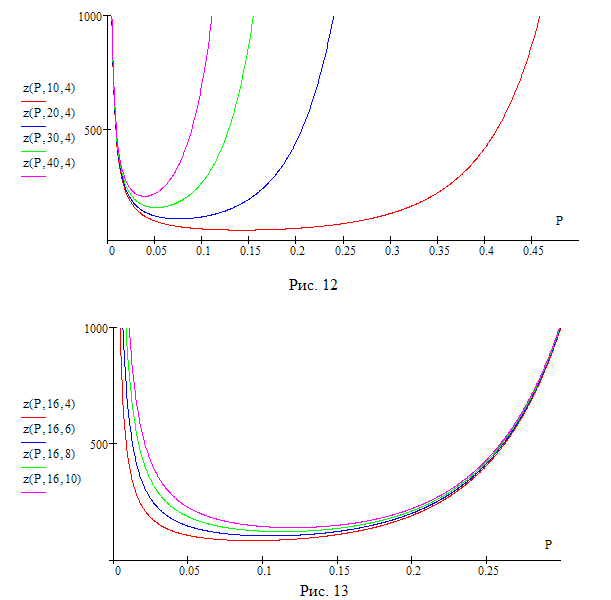
Графики ясно показывают, что наибольшее влияние на среднюю продолжительность цикла оказывает релаксационное число. При средняя продолжительность цикла увеличивается до бесконечности, поскольку невозможен выход из фазы выборочного контроля. При невозможен выход из фазы сплошного контроля, поэтому продолжительность цикла вновь увеличивается до бесконечности. При некотором значении средняя продолжительность цикла достигает минимального значения. Для определения этого значения входного уровня дефектности следует продифференцировать выражение для средней продолжительности цикла и приравнять производную нулю. В результате получается равенство:

Первые два слагаемых во втором выражении определяют величину , поэтому минимальная продолжительность цикла контроля составит или, с помощью третьего выражения, .

Это выражение будет использовано в следующем пункте.

4. Средняя доля контролируемых изделий

Среднее число контролируемых за цикл изделий складывается из двух составляющих:

- в фазе сплошного контроля – все изделия, то есть ,

- в фазе выборочного контроля – k-тая доля изделий, то есть .

Поэтому в среднем в каждом цикле контролируется доля изделий, равная

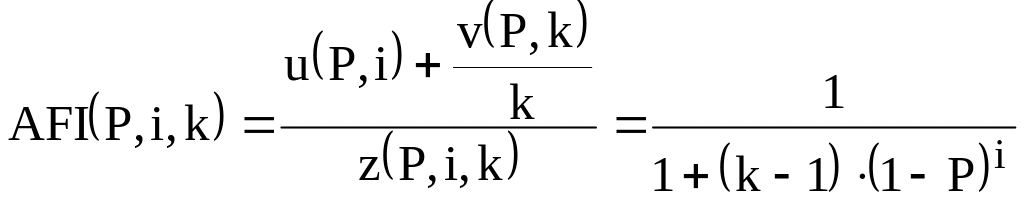
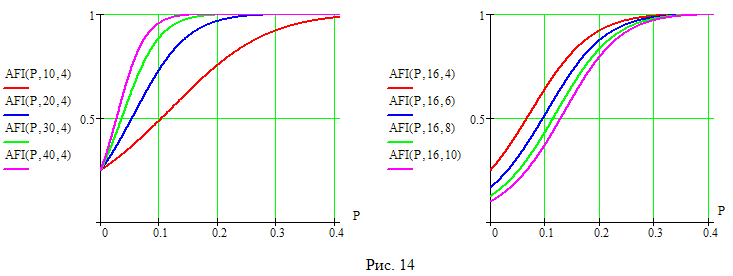
На рис. 14 показаны графики зависимости средней доли контролируемых изделий от уровня дефектности при различных значениях параметров плана i и k. Средняя доля контролируемых изделий быстро возрастает, и уже при уровнях дефектности, больших 10%, превышает 50% практически при любых планах контроля.

5. Средний выходной уровень дефектности

Средний выходной уровень дефектности – это доля брака среди изделий, изготовленных при использовании плана CSP1. Ее можно определить как отношение среднего числа дефектных изделий, прошедших через сито контроля за время цикла, к средней продолжительности цикла контроля. В фазе сплошного контроля все дефектные изделия заменяются годными, а в фазе выборочного контроля необнаруженными оказывается в среднем дефектных изделий (дефектное изделие, служащее сигналом к переходу в фазу сплошного контроля, обнаруживается и заменяется годным). Поэтому средний выходной уровень дефектности для плана CSP1 можно определить как:

.

Средний выходной уровень дефектности с ростом k монотонно стремится к значению входного уровня дефектности Р, а с ростом релаксационного числа i – к нулю. Зависимость от входного уровня дефектности оказывается более сложной (рис. 15).

При некотором значении входного уровня дефектности , который минимизирует среднюю продолжительность цикла контроля, выходной уровень дефектности достигает максимального значения. Это значения носит название предела среднего выходного уровня дефектности, которое составляет:

.

С учетом ранее полученного выражения находим простое выражение для среднего выходного уровня дефектности производственного процесса:

.

К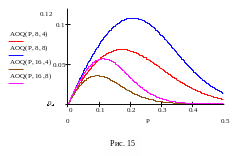 аким бы ни был входной уровень дефектности, ее выходной уровень всегда будет меньше предельного значения , определяемого параметрами плана контроля.