7.5.2. Описание отклика нелинейного элемента в частотной области

Воспользуемся для описания нелинейного элемента степенным рядом. В этом случае отклик во временной области нелинейного элемента будет описываться следующим соотношением:

2.58

Для отображения уравнения (2.58) в частотную область воспользуемся преобразованием Фурье:

В итоге получим: Фурье образ k-ой параболы входного сигнала Х(jw), входящий в уравнение (2.59), можно рассматривать как k-кратную автосвёртку обычного комплексного спектра Х(jw):

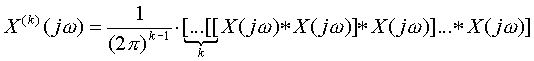
где каждая операция свертки (*) является определенным интегралом в бесконечных пределах:

Подобная интерпретация Фурье образа базируется на том, что (k) операций умножения во временной области при переходе в частотную превращаются в (k) операций свертки. В результате попытки построить Фурье-образ из обычных спектров Х(jw) приводят к необходимости длительного и подчас некорректного вычисления многократных интегралов. Именно по этой причине прямое явное вычисление в частотной области Фурье- образов через автосвертки нежелателен.

Гораздо более рациональным является вычисление спектров в неявной форме в момент осуществления преобразования Фурье:

На практике интеграл Фурье всегда вычисляют по конечным пределам, а комплексную экспоненту разлагают на косинусную и синусную составляющие по формуле Эйлера:

Косинусная и синусная части комплексного спектра вычисляются раздельно и эти спектры, вычисленные на конечном интервале наблюдения, оказываются дискретными:

где

Процедуру вычисления спектров можно рассматривать двояко: можно рассматривать эту операцию как линейную по отношению к исходной параболе , можно подойти к вопросу иначе и рассматривать эту процедуру как некоторое обобщенное нелинейное преобразование Фурье по отношению к исходному сигналу х(t). И та и другая интерпретация возможны и имеют свои определенные преимущества.

Следует отметить, что впервые преобразования вида использовал Вебер [15]. Именно он в 1955 году первым осознал преимущества, которые дает простое и компактное описание нелинейного элемента в частотной области (2.59). Однако, в то время предложенный Вебером подход не получил широкого распространения, так как Вебер преобразования вида вычислял аналитически. Сегодня появилась возможность исключить громоздкие и требующие высокой квалификации аналитические расчеты. С появлением персональных компьютеров операция вычисления преобразований численными методами превратилась в элементарную рутинную процедуру.

Справедливости ради следует подчеркнуть, что возможно Вебер был далеко не первым, осознавшим все преимущества преобразований вида . Может оказаться, что этого вида преобразованиями пользовался еще Хевисайд, однако этого нельзя утверждать однозначно, так как последний труд Хевисайда, посвященный нелинейным электрическим цепям, был утерян после его смерти. В этой работе, судя по воспоминаниям читавших ее фрагменты, Хевисайд давал очень простое аналитическое описание нелинейных электрических цепей. Подобное простое описание нелинейных цепей невозможно получить, используя линейные операторы Лапласа X(p). Переход же к нелинейным операторам сразу все упрощает. Хевисайд фактически является автором операторного метода, который сегодня принято называть методом Лапласа. Преобразования Лапласа правильнее называть преобразованиями Хевисайда, так как именно он является автором основной идеи. Некоторое время операторный метод Хевисайда не имел строгого обоснования, и только в 1915 Бромвич доказал его корректность через использование интегралов Лапласа или контурных интегралов в комплексной области [57,58].