10. Метод ветвей и границ.

Метод ветвей и границ является специальным частным случаем метода поиска с ограничением. Этот метод успешно применяется ко многим задачам, в том числе и к NP-полным. Основная идея метода такова: необходимо все огромное количество переборов разделить на классы и определить оценки для этих классов (снизу – для задач минимизации, сверху – для задач максимизации), для того чтобы иметь возможность отбрасывать возможные решения не по одному варианту, а сразу целыми классами.

Трудность этого метода заключается в том, чтобы найти такое разбиение на классы (ветви) и так определить для них оценки (границы), чтобы процедура была эффективной. По сути метод ветвей и границ представляет собой организованный перебор, в ходе выполнения которого исходная задача делится на множество подзадач, которые, в свою очередь, также делятся на подзадачи и так далее, до тех пор, пока не будет найдено решение.

Например, при применении этого метода к задаче о коммивояжере для городов данная задача разбивается на подзадачу. Первая подзадача – должна содержать траектории с ребром между городами , вторая - с ребром . Затем первое множество разбивается на подзадачи, первая из которых должна содержать траектории с ребрами , , а вторая , .

Для каждой из подзадач (ветви) вычисляются два числа – оценки (границы). Нижняя граница – это лучшее решение, верхняя граница – это худшее решение. Далее, перед следующим разбиением, на основе полученных чисел возникает возможность исключения некоторых подзадач, если полученная нижняя граница меньше верхней. В этом случае, решения для этой подзадачи не являются оптимальными для исходной задачи.

Ограничения в методе ветвей и границ основываются на предположении, что на множестве возможных и частичных решений задана некоторая функция цены и, что нужно найти решение наименьшей стоимости. Для применения этого метода функция цены должна обладать тем свойством, что стоимость частичного решения не может быть выше, чем стоимость расширения данного частичного решения.

В большинстве случаев функция цены не является отрицательной и даже удовлетворяет более сильному требованию: .

Это свойство позволяет отбрасывать те решения, стоимость которых оказалась выше, чем стоимость решения, полученного на предыдущем шаге. В этом случае в качестве кандидата на новое ветвление выбирается множество с наименьшей оценкой. На каждой итерации алгоритма и для каждого подмножества вычисляется верхняя и нижняя оценки. Нижнюю оценку получают решением задачи точным методом, верхнюю оценку - с помощью какого-либо эвристического алгоритма.

Метод ветвей и границ – это не один специальный вид алгоритмов, это целый класс алгоритмов. Его эффективное использование зависит от разработки способов разбиения пространства решение, то есть от структуры ветвления и от используемых алгоритмов для определения оценок.

11. Остовные деревья графа. Алгоритмы нахождения дерева минимального веса: алгоритм Прима, алгоритм Крускала.

Остовное дерево: Пусть имеется связный неориентированный граф . Для каждого ребра графа задан вес . Связный подграф графа , являющийся деревом и содержащий все вершины, называют покрывающим (остовным) деревом (spanning tree, остов). Задача о нахождении покрывающего дерева может быть решена при помощи алгоритмов обхода в глубину и в ширину. Задача о нахождении минимального покрывающего дерева состоит в нахождении подмножества , связывающего все его вершины, для которого суммарный вес 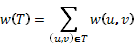минимален. Такое подмножество должно быть деревом. Остовное дерево является связным графом, таким образом, из любой вершины в остовном дереве можно добраться до любой другой вершины. В остовном дерево находится вершин и ребро!

В полном графе с вершинами существует остовных деревьев. В одном и том же графе можно построить несколько остовных деревьев, в некоторых случаях, несколько остовных деревьев минимального веса.

Алгоритм Прима: В алгоритме Прима растущая часть остова представляет собой дерево. Формирование дерева начинается с произвольной корневой вершины . На каждом шаге добавляется ребро наименьшего веса среди ребёр, соединяющих вершины этого дерева с вершинами не из дерева. В результате получается минимальный остов.

Очередь с приоритетом служит для хранения вершин, не попавших пока в дерево. Приоритет вершины определяется значением , которое равно минимальному весу ребра, соединяющего с вершинами дерева. Ребра остовного дерева собираются в массиве предшественников . Очевидно, что количество ребер в нем есть , так как корневая вершина своего предшественника не имеет.

Алгоритм Крускала: Построение дерева начинается с создания графа , который содержит все вершины исходного графа, но не содержит ни одного ребра. В любой момент работы алгоритма Крускала множество выбранных ребер не содержит циклов. Оно соединяет вершины графа в несколько связных компонент, каждая из которых является деревом. Объединение всех компонент в одну компоненту и приводит к созданию остовного дерева.

Первым шагом является сортировку множества ребер по возрастанию. Выбор ребра происходит от меньшего к большему. На каждом шаге ребро анализируется: если оно соединяет две вершины из разных компонент связности, то ребро включается в множество ребер остовного дерева, если же ребро соединяет две вершина из одной компоненты связности, то оно пропускается (иначе порождается цикл). Исходно имели компонент связности, осталась только одна, таким образом, было связано компонента ребром.

Здесь является множеством ребер остовного дерева. Каждая вершина имеет указание на уникальный идентификатор множества (компоненты связности), создаваемый . Для проверки принадлежности двух вершин одной компоненте связности используется , которая и возвращает этот идентификатор. Процедура объединяет два множества, делая их идентификаторы одинаковыми.