6. Эйлеров путь, эйлеров цикл, эйлеров граф. Алгоритм нахождения эйлерова цикла.

Эйлеров граф. Эйлеров путь. Эйлеров цикл. Алгоритм нахождения Эйлерова цикла.

Эйлеровым путем в графе называется произвольный путь, проходящий через каждое ребро графа в точности один раз.

Эйлеров цикл соответствует обходу всех ребер графа, причем каждое ребро при таком обходе проходится один раз и только в одном направлении. Граф, в котором существует Эйлеров цикл, называется Эйлеровым графом.

Необходимое и достаточное условие Эйлерова пути.

Эйлеров путь существует в графе  когда граф связный и содержит не более чем 2 вершины нечетной степени.

Условие существования Эйлерова цикла

~ существует в графе, когда граф связный и в нём отсутствуют вершины нечетной степени.

Алгоритм нахождения Эйлерова цикла в графе

Пусть дан граф G=<V,E>, который связан и степень вершин которого имеют четную степень. Граф представлен списками инцидентности (lec[V])

Для промежуточного хранения используется стек STEC

Для хранения Эйлерово цикла используется стек CE.

1. STEC=0; CE=0;

2. V=V₀ – произвольная начальная вершина

3. STEC <= V – занесение вершины в стек

4. while(STEC) do

5. V=TOP(STEC); - взять значение вершины стека

6. if (rec[V]) then do

7. U = V₁ – первый элемент в списке rec[V]

8. STEC <= U;

9. rec[v] = rec / U; rec[U] = rec[U] / V; удаление ребра [V,U]

10. V=U; end

11. else V <= Stec; CE <= V; если rec[V]=0;

Принцип действия алгоритма можно обьяснить следующим образом: пусть V₀ – вершина, выбранная в строке 2. Цикл while начинает строить этот путь сначала в V₀, причем вершина этого пути помещается в промежуточный стек , а рёбра удаляются из графа. Эти действия продолжаются до момента, когда путь нельзя удлинить, включив в него новую вершину. В этот момент, когда путь нельзя удлинить, у нас должно быть что V = V₀ .

На этот момент из нашего графа удалён цикл С₁ и вершины этого цикла находятся в промежуточном стеке. Если в цикл С₁ вошли все рёбра графа, то С₁ является эйлеровым циклом. Если в цикл С₁ вошли не все рёбра графа, то в оставшемся графе степень произвольной вершины останется четной. Вершину V = V₀ переносим из промежуточного стека в результирующий (11), и процесс продолжается с очередной вершины V, которая является верхним элементом промежуточного стека. Эти действия продолжаются до момента, пока промежуточный стек не опустеет. По окончанию алгоритма, результирующий стек содержит эйлеров цикл.

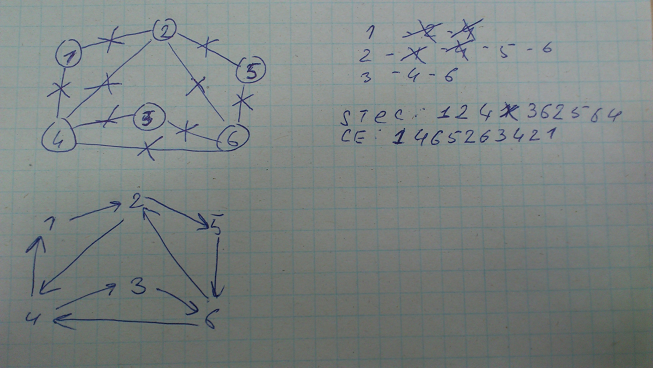
Сложность алгоритма в худшем случае O(n^2)

7. Нахождение кратчайших расстояний. Алгоритм Дейкстры.

Задачи о кратчайших путях относятся к фундаментальным задачам комбинаторной оптимизации, так как многие такие задачи можно свести к отысканию кратчайшего расстояния и пути. Существуют различные типы задач о кратчайшем пути. Например, между двумя заданными вершинами, между данной вершиной и всеми остальными вершинами графа, между каждой парой вершин в графе, между двумя заданными вершинами для путей, проходящих или, наоборот, непроходящих через одну или несколько заданных вершин. Найти первый, второй и тд кратчайшие пути в графе.

Одним из лучших алгоритмов для отыскания кратчайшего пути принадлежит Дейкстре и был предложен в 1959 году. С помощью этого алгоритма можно решить следующую задачу:

Пусть дан граф G = <V, E>, к ребрам которого приписаны положительные веса. И требуется найти кратчайшее расстояние между фиксированной парой вершин S и T. В алгоритме Дейкстры выделяют две части:

1. Отыскание длины кратчайшего пути методом расстановки меток.

2. Отыскание собственно пути обратным ходом.

В процессе работы алгоритма вершинам графа приписываются метки, которые подразделяются на постоянные и временные. Постоянная метка приписывается вершине, до которой на текущем шаге найдено кратчайшее расстояние. Обозначим такую вершину через y. Временные метки X присваиваются вершинам, до которых пока не найдено кратчайшее расстояние.

Перед началом работы алгоритма все вершины имеют временные метки d(x) = ∞.

Зададим граф матрицой смежности, в которой a(I, J) = d(I, J), если ребро (I, J) существует.

a(I, J) = ∞, если ребро (I, J) не существует.

a(I, I) = 0, для всех I = 1…N

Алгоритм:

1. Выбираем начальную вершину S и присваиваем вершине S постоянную метку:

y = S

d(S) = 0

Всем остальным вершинам: d(x) = ∞.

2. Для всех вершин X, смежных с Y, и не имеющих постоянной метки, пересчитаем величины d(x) по следующей формуле:

d(x) = min{ d(x), d(y)+a(a, x) }

(1)

2/ |1

(S)4— (3)

5\ |1

(2)

d(1) = min { d(x), d(y) + a(y,x) } = min { d(1). d(S) + a(S, 1) } = min { ∞, 0 + 2 } = 2

d(2) = 5

d(3) = 4

Проверяем, если все d(x) = ∞, для всех непомеченных вершин X, то надо закончить процедуру работы алгоритма, так как в исходном графе отсутствуют пути из S помеченной вершины, В противном случае, выбрать ту из вершин X, которая имеет наименьшую временную метку.

3. Проверяем, если Y = T, закончить работу алгоритма, так как кратчайший путь из S в T найден. В противном случае перейти к шагу 2.

Простое изменение этого алгоритма позволит получить кратчайшие пути от S ко всем остальным вершинам графа, для этого нужно изменить правила остановки. Останавливаться не при Y = T, а в случае когда все пометки станут постоянными. Трудоемкость алгоритма при таком изменении не возрастет, так как вершина T в самом худшем случае получает постоянную метку самой последней, а в этой ситуации число шагов работы обоих алгоритмов одинаковы. Сложность алгоритма Дейкстры O(N^2).

С помощью рассмотренного алгоритма мы нашли расстояние между выделенными вершинами, а не сам путь. Однако, зная расстояние, мы можем при условии положительной длины всех контуров определить все кратчайшие пути. Для этого достаточно отметить, что для произвольных вершин S и T. Существует некоторая вершина V такая, что d(S,T) = d(S,V) + a(V,T). Таким свойством обладает произвольная вершина из S в T.

d(S,V) = d(S,V) - a(V,T)

Мы можем найти такую вершину U, для которой d(S,V) = d(S,U) + a(U,T).

Из положительной длины всех контуров следует, что созданная таким образом последовательность.

T → V → U … → S

Не содержит повторений и оканчивается на S. Она при обращении очередности и определяет кратчайший путь из S в T.

Опишем другой вариант реализации алгоритма Дейкстра.

Алгоритм использует три массива, каждый размерности N, где N - число вершин.

Массив А - содержит метки с двумя значениями. (0 - временная метка, 1 - )

Массив B - содержит текущее кратчайшее расстояние от вершины S до соответствующей вершины.

Массив C - содержит номера вершин, причем Ck - номер предпоследней вершины на текущем кратчайшем пути из S в T. Матрица смежности так же, как и в первом случае.

Основные шаги алгоритма:

1. Перед началом работы заполняем массив A нулями, массив B значением бесконечность, массив C = 0.

Пусть i - номер начальной вершины (S).

Присвоим a[i] = a[S] = 1 (обозначаем как помеченную).

c[i] = 0.

Перенесем i-ую строку матрицы смежности в массив B.

Заполним числом i массив C.

2. Найти минимум среди непоченных вершин, для которых a[k] = 0. Пусть этот минимум достигается на индексе j.

b[j] = min{ b[k] }

a[j] = 1

bk = min { bk, bj + djk }

Если bk > bj + djk = > bk = bj + djk

Если a[k] = 0 или a[t] = 0, то работа по нахождению кратчайшего расстояния закончена и длина пути от Vi до Vk равна Vk.

3. Определение самого пути.

3.1. Напечатать T

3.2. z = c[t]

3.3. Напечатать z

3.4. z = c[z]

Проверить, если z=0, то закончить выдачу ответа, иначе перейти к шагу 3.3