4. Сферы применения графов. Способы машинного представления графов, их достоинства и недостатки.

Графы и алгоритмы на графах.

Графы являются обобщенными иерархическими структурами, и обычно обозначаем G=<V,E>

V- множество рёбер

E- множество вершин

Способы машинного представлении графа

Рассмотрим несколько способов представления графа с оценкой их достоинст и недостатков.

1. Классический способ представления графов – матрица инциденций.

~ это матрица Aij (n*m), где n – число строк, соответствует числу вершин, а m – число столбцов, которое равно числу рёбер.

В случае неориентированного графа столбец, соответствующий ребру [Vi, Vj] содержит единицу, в строках, соответствующим вершинах Vi и Vj, а в остальных нули.

Для ориентированного графа, столбец, соответствующий дуге <Vi, Vj> содержит -1 в строке, соответствующей вершине Vi и 1 в строке, соответствующей вершине Vj.

С алгоритмической точки зрения матрица инциденций явзяется самым худшем способом представления графа, т.к.:

1. требует n*m ячеек памяти, большинство из них заполнены нулями

2. неудобен доступ к информации, т.к. определение существует ли какая либо дуга требует в худшем случае перебор всех столбцов матрицы, следовательно, m шагов.

2. Матрица смежности (Aij), в которой

Aij=1, если существует ребро (i,j)

Aij=0, если не существует ребро (i,j)

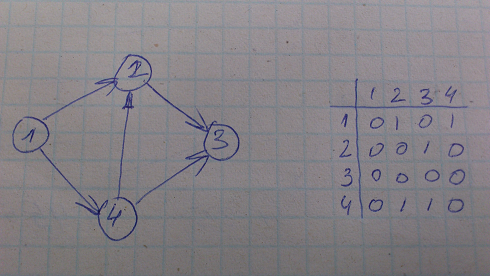
Недостаток: размер занятой памяти n*n

3. С помощью списка пар соответствующих его рёбрам (более экономным по отношении к памяти, особенно в случае неплотных графов, когда m<n*n).

Неудобство: большое число шагов, необходимое для получения множества вершин, которым ведут рёбра из данной вершины.

4. Списки инцидентности – в этом способе представления графа каждая вершина ассоциируется со связным списком смежных с ней вершин.

Это динамическая модель хранит информацию лишь о фактически принадлежащих графу вершинах.

5. Алгоритмы поиска в графе: поиск в ширину, поиск в глубину.

Способы прохождения графа

Существуют много алгоритмов на графах, в основе которых лежит систематический перебор вершин графа такой, что каждая вершина просматривается в точности один раз.

Рассмотрим два алгоритма поиска в графе: поиск в глубину и поиск в ширину.

1. поиск в грубину:

Начальная вершина передаётся в качестве параметра и становится первой обрабатываемой вершиной, далее начинается итерационный процесс на каждом шаге которого ищутся смежные вершины, которые запоминаются в стеке для того, чтобы можно было к ним вернуться и продолжить поиск к другому пути в случае, если мы достигли тупика и еще остались необработанные вершины.

Обработанные вершины образуют множество всех вершин, достижимых из начальной вершины.

Пусть имеется стек для хранения смежных вершин – S и список – L для хранения обработанных вершин.

Алгоритм:

1. поместим начальную вершину в стек

2. начинаем итерационный процесс, выталкивая вершины из стека и её обработки. На каждой итерации используется следующая стратегия:

   1. вытолкнуть вершину V из стека

   2. проверить по списку L, была ли она обработана. Если нет, провести обработку этой вершины, включив её в список Lчтобы избежать повторной обработки. А также поместить в стек те смежный с V вершины, которых еще нет в списке L. Процесс завершается, когда стек становится пустым. На этот момент список L содержит список обработанных вершин.

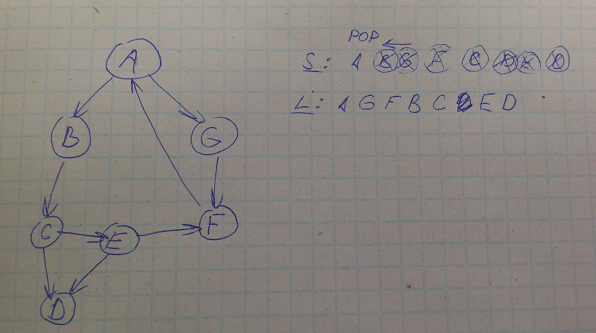
Способ прохождения графа не единственен.

2. Поиск в ширину (Поиск сначала) – при данном поиске начиная с некоторой начальной вершины производится обработка каждой смежной с ней вершиной. Затем, сканирование продолжается на следующем уровне смежных вершин и так до конца пути (до просмотра всех вершин), при этом запоминании следующих вершин используется очередь.

Т.е. поиск в ширину основывается на замене стека очередью.

Чем раньше помещается вершина, тем раньше она используется. Использование вершины происходит с помощью просмотра сразу всех еще непросмотренных соседей вершины и её занесение в результирующий список.

Och – очередь для промежуточного хранения

L – для хранения результирующего списка

Начальная вершина заносится в очередь. Начинается итерационный процесс на каждом шаге которого выполняются следующие действия:

2.1. Удалить вершину V из очереди;

2.2. Проверить её наличие в списке обработанных вершин. Если вершины V нет в списке L, включить её в этот список;

2.3. Одновременно, получить все смежные в V вершины и вставить в очередь те из них, которые отсутствуют в списке обработанных вершин;

Итерационный процесс продолжается до тех пор, пока очередь не опустеет.

Оба вида поиска в графе могут быть использованы:

1. Для нахождения остового дерева;

2. Для нахождения пути между фиксированными вершинами V и U (для этого достаточно начать поиск в графе с вершины V и вести его до момента посещения вершины U);