Примеры и контрпримеры

Формулы в КНФ:

Формулы не в КНФ:

Но эти 3 формулы не в КНФ эквивалентны следующим формулам в КНФ:

Построение кнф Алгоритм построения кнф

1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:

2) Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул:

3) Избавиться от знаков двойного отрицания.

4) Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.

Пример построения кнф

Приведем к КНФ формулу

Преобразуем формулу F к формуле не содержащей → :

В полученной формуле перенесем отрицание к переменным и сократим двойные отрицания:

По закону дистрибутивности получим КНФ:

Переход от кнф к скнф

Если в простой дизъюнкции не хватает какой-то переменной (например, z), то добавляем в нее выражение : (это не меняет самой дизъюнкции), после чего раскрываем скобки с использованием распределительного закона:

Таким образом, из КНФ получена СКНФ.

34. Полином Жегалкина — многочлен над кольцом , то есть полином с коэффициентами вида 0 и 1, где в качестве произведения берётся конъюнкция, а в качестве сложения — исключающее или. Полином был предложен в 1927 году Иваном Жегалкиным в качестве удобного средства для представления функций булевой логики. В зарубежной литературе представление в виде полинома Жегалкина обычно называется алгебраической нормальной формой (АНФ).

Теорема Жегалкина — утверждение о существовании и единственности представления всякой булевой функции в виде полинома Жегалкина.

Полином Жегалкина представляет собой сумму по модулю два произведений неинвертированных переменных, а также (если необходимо) константы 1. Формально полином Жегалкина можно представить в виде

или в более формализованном виде как:

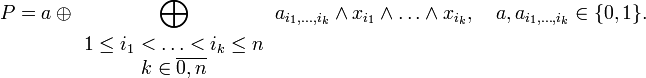
Примеры полиномов Жегалкина:

Предпосылки

По теореме Поста, чтобы система булевых функций была полной, надо, чтобы в ней существовали:

1. Хотя бы одна функция, не сохраняющая 0.

2. Хотя бы одна функция, не сохраняющая 1.

3. Хотя бы одна нелинейная функция.

4. Хотя бы одна немонотонная функция.

5. Хотя бы одна несамодвойственная функция.

Этому требованию отвечает система функций . На её основе и строятся полиномы Жегалкина.

Cуществование и единственность представления

По теореме Жегалкина каждая булева функция единственным образом представляется в виде полинома Жегалкина. Теорема доказывается следующим образом. Заметим, что различных булевых функций от n переменных штук. При этом конъюнкций вида существует ровно 2ⁿ, так как из n возможных сомножителей каждый или входит в конъюнкцию, или нет. В полиноме у каждой такой конъюнкции стоит 0 или 1, то есть существует различных полиномов Жегалкина от n переменных. Теперь достаточно лишь доказать, что различные полиномы реализуют различные функции. Предположим противное. Тогда приравняв два различных полинома и перенеся один из них в другую часть равенства, получим полином, тождественно равный нулю и имеющий ненулевые коэффициенты. Тогда рассмотрим слагаемое с единичным коэффициентом наименьшей длины, то есть с наименьшим числом переменных, входящих в него (любой один, если таких несколько). Подставив единицы на места этих переменных, и нули на места остальных, получим, что на этом наборе только одно это слагаемое принимает единичное значение, то есть нулевая функция на одном из наборов принимает значение 1. Противоречие. Значит, каждая булева функция реализуется полиномом Жегалкина единственным образом.

Представление функции в виде полинома Жегалкина

С помощью эквивалентных преобразований ДНФ

По сравнению с ДНФ в полиноме Жегалкина отсутствуют операции ИЛИ и НЕ. Таким образом, полином Жегалкина можно получить из ДНФ, выразив операции ИЛИ и НЕ через операции сложение по модулю два, и константу 1. Для этого применяются следующие соотношения:

Ниже приведён пример преобразования ДНФ в полином Жегалкина:

При преобразованиях использованы соотношения:

С помощью эквивалентных преобразований СДНФ

СДНФ обладает тем свойством, что при любых значениях входных переменных в единицу обращается не более одного члена выражения. Для таких выражений операция дизъюнкции эквивалентна операции сложение по модулю два.

При преобразовании СДНФ в полином Жегалкина, достаточно заменить все дизъюнкции на операции сложение по модулю два и избавиться от инверсий при помощи эквивалентного преобразования

С помощью карты Карно

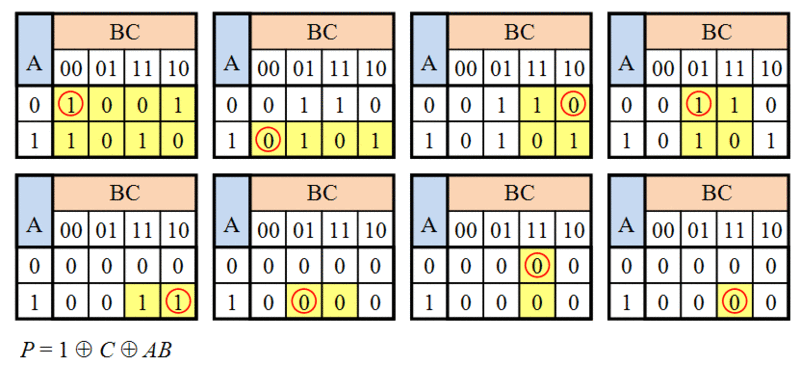
Логическая функция трёх переменных , представленная в виде карты Карно, преобразуется в полином Жегалкина следующими шагами:

• Рассматриваем все ячейки карты Карно в порядке возрастания количества единиц в их кодах. Для функции трёх переменных последовательность ячеек будет 000—100 — 010—001 — 110—101 — 011—111. Каждой ячейке карты Карно сопоставляем член полинома Жегалкина в зависимости от позиций кода, в которых стоят единицы. Например, ячейке 111 соответствует член ABC, ячейке 101 — член AC, ячейке 010 — член B, ячейке 000 — член 1.

• Если в рассматриваемой ячейке находится 0, переходим к следующей ячейке.

• Если в рассматриваемой ячейке находится 1, добавляем в полином Жегалкина соответствующий член, инвертируем в карте Карно все ячейки, где этот член равен 1 и переходим к следующей ячейке. Например, если при рассмотрении ячейки 110 в ней оказывается единица, то в полином Жегалкина добавляется член AB и инвертируются все ячейки карты Карно, где A=1 и B=1. Если единице равна ячейка 000, то в полином Жегалкина добавляется член 1 и инвертируется вся карта Карно.

• Процесс преобразования можно считать законченным, когда после очередной инверсии все ячейки карты Карно становятся нулевыми.

Пример преобразования таблицы истинности в полином Жегалкина для функции трёх переменных