
- •28. Свойства логических операций
- •Примеры и контрпримеры
- •Построение днф Алгоритм построения днф
- •Пример построения днф
- •Переход от днф к сднф
- •Примеры и контрпримеры
- •Построение кнф Алгоритм построения кнф
- •Пример построения кнф
- •Переход от кнф к скнф
- •Предпосылки
- •Cуществование и единственность представления
- •Метод треугольника
- •Трёхзначные логики
- •Четырёхзначные логики
- •Конечнозначные логики
- •Бесконечнозначные логики
- •37. Перестановочный шифр
- •Пример (шифр Древней Спарты)
- •Шифры простой замены
- •Примеры шифров простой замены Шифр Атбаш
- •Шифр с использованием кодового слова
- •Безопасность шифров простой замены
- •Омофоническая замена
- •Примеры омофонических шифров Номенклатор
- •Великий Шифр Россиньоля
- •Книжный шифр
- •Криптоанализ
- •Математическая модель
- •Префиксные коды
- •40. Необходимые и достаточные условия существования префиксного кода с заданными длинами кодовых слов. Неравенство Крафта
- •41. Оптимальное кодирование, свойства оптимальных кодов, построение оптимальных кодов методом Хафмена
- •42. Передача данных и кодирование информации
- •Коды обнаружения и исправления ошибок
- •43. Коды обнаружения и исправления ошибок
- •Блоковые коды
- •Линейные коды общего вида
- •Минимальное расстояние и корректирующая способность
- •Коды Хемминга — простейшие линейные коды с минимальным расстоянием 3, то есть способные исправить одну ошибку. Код Хемминга может быть представлен в таком виде, что синдром
- •Общий метод декодирования линейных кодов
- •Линейные циклические коды
- •Порождающий (генераторный) полином
- •Коды crc
- •Преимущества и недостатки свёрточных кодов
- •Каскадное кодирование. Итеративное декодирование
- •Примеры
- •Свойства
- •История
- •Систематические коды
- •Самоконтролирующиеся коды
- •Самокорректирующиеся коды
- •Литература
- •Код Хемминга
- •Алгоритм
- •Другие способы описания
- •Детерминированность
- •Автоматы и регулярные языки
- •Специализированные языки программирования
- •Разработка моделей с использованием конечных автоматов
- •Принцип построения
- •Способы получения минимальной формы
- •Граф переходов
- •Матрица переходов
- •Свойства минимальной формы
- •Термины
- •Порождающие грамматики
- •Типы грамматик
- •Применение
- •Пример — арифметические выражения
- •Аналитические грамматики
- •Классификация грамматик
- •Классификация языков
- •8.2. Устранение эпсилон-правил
- •8.3. Нормальная форма Хомского
25. Алгебра логики (алгебра высказываний) — раздел математической логики, в котором изучаются логические операции над высказываниями[1]. Чаще всего предполагается (т. н. бинарная или двоичная логика, в отличие от, например, троичной логики), что высказывания могут быть только истинными или ложными.
Булева функция (функция алгебры логики) — функция, определённая на множестве упорядоченных наборов из нулей и единиц и принимающиая на каждом из этих наборов значение 0 или 1.
Переменная xi функции f (x1, …, xn) называется существенной, если существуют такие два набора из нулей и единиц, различающиеся только в i-й компоненте, что функция f на этих наборах принимает различные значения. В этом случае говорят, что функция f (x1, …, xn) существенно зависит от переменной xi. Переменная xi, не являющаяся существенной, называется несущественной или фиктивной переменной функции f (x1, …, xn); в этом случае говорят, что функция f (x1, …, xn) не зависит существенно от переменной xi.
Например, функция f (x1, x2) = x1 x2 существенно зависит от переменной x1, так как f (0, 1) ≠ f (1, 1). Она также существенно зависит от переменной x2, так как f (1, 0) ≠ f (1, 1). Аналогично показывается, что все функции, приведённые в табл. 2, существенно зависят от обеих переменных. Очевидно, что константы 0 и 1 не имеют существенных переменных.
Значение функции на каждом наборе полностью определяется набором значений её существенных переменных. В связи с этим часто для удобства использования (и следуя возникшей традиции) понятие равенства распространяется также на функции, отличающиеся лишь несущественными переменными, и понимается следующим образом. Две функции называются равными, если у них множества существенных переменных совпадают и на каждом наборе значений этих переменных рассматриваемые функции принимают одинаковые значения.
Таким образом, всякое множество булевых функций вместе с каждой функцией содержит также и все функции, которые отличаются от исходной лишь фиктивными переменными. То есть фактически определяется операция введения фиктивной переменной на рассматриваемом множестве функций.
Определение
Базовыми элементами,
которыми оперирует алгебра логики,
являются высказывания.
Высказывания строятся над множеством
{B,
![]() ,
,
![]() ,
,
![]() ,
0, 1}, где B — непустое множество, над
элементами которого определены три
операции:
,
0, 1}, где B — непустое множество, над
элементами которого определены три
операции:
отрицание (унарная операция),
конъюнкция (бинарная),
дизъюнкция (бинарная),
а также константы — логический ноль 0 и логическая единица 1.
Дизъюнкт —
пропозициональная
формула, являющаяся дизъюнкцией
одного или более литералов
(например
![]() ).
Конъюнкт —
пропозициональная
формула, являющаяся конъюнкцией
одного или более литералов (например
).
Конъюнкт —
пропозициональная
формула, являющаяся конъюнкцией
одного или более литералов (например
![]() ).
).
Аксиомы
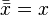 ,
инволютивность
отрицания, закон
снятия двойного отрицания
,
инволютивность
отрицания, закон
снятия двойного отрицания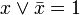
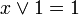
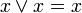
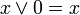
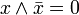
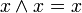
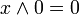
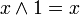
Логические операции
Простейшим и наиболее широко применяемым примером такой алгебраической системы является множество B, состоящее всего из двух элементов:
B = { Ложь, Истина }
Как правило, в математических выражениях Ложь отождествляется с логическим нулём, а Истина — с логической единицей, а операции отрицания (НЕ), конъюнкции (И) и дизъюнкции (ИЛИ) определяются в привычном нам понимании. Легко показать, что на данном множестве B можно задать четыре унарные и шестнадцать бинарных отношений и все они могут быть получены через суперпозицию трёх выбранных операций.
Опираясь на этот
математический инструментарий, логика
высказываний изучает высказывания
и предикаты.
Также вводятся дополнительные операции,
такие как эквивалентность
![]() («тогда
и только тогда, когда»), импликация
(«тогда
и только тогда, когда»), импликация
![]() («следовательно»),
сложение по модулю два
(«следовательно»),
сложение по модулю два
![]() («исключающее
или»), штрих
Шеффера
(«исключающее
или»), штрих
Шеффера
![]() ,
стрелка
Пирса
,
стрелка
Пирса
![]() и
другие.
и
другие.
Логика
высказываний послужила основным
математическим инструментом при создании
компьютеров. Она легко преобразуется
в битовую
логику: истинность высказывания
обозначается одним битом (0 — ЛОЖЬ,
1 — ИСТИНА); тогда операция
![]() приобретает
смысл вычитания из единицы;
—
немодульного сложения; & — умножения;
—
равенства;
—
в буквальном смысле сложения по модулю
2 (исключающее Или — XOR);
—
непревосходства суммы над 1 (то есть A
B
= (A + B) <= 1).
приобретает
смысл вычитания из единицы;
—
немодульного сложения; & — умножения;
—
равенства;
—
в буквальном смысле сложения по модулю
2 (исключающее Или — XOR);
—
непревосходства суммы над 1 (то есть A
B
= (A + B) <= 1).
Впоследствии булева алгебра была обобщена от логики высказываний путём введения характерных для логики высказываний аксиом. Это позволило рассматривать, например, логику кубитов, тройственную логику (когда есть три варианта истинности высказывания: «истина», «ложь» и «не определено») и др.
26. Определение. Суперпозицией функций f1, … , fm называется функция f,
полученная с помощью подстановок этих функций друг в друга и переименования переменных.
Пример. Пусть даны функции f1( x1, x2 ) = ( 0, 1, 1, 0 ) и f2( x1, x2 ) = (1, 0, 1, 0).
Тогда функция f( x2, x3, x4 ) = f1[ x2, f2(x3, x4) ] будет суперпозицией функций f1 и f2.
Таблица 1.8
x2 |
х3 |
х4 |
f2(x3, x4) |
f=f1[x2, f2(x3, x4)] |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
f( x2,x3,x4 ) = ( 1,0,1,0,0,1,0,1 ).
Определение. Формулой алгебры логики называется выражение, описывающее суперпозицию логических функций.
Например, формула
F = f3{ f1( x3,x1 ), f2[ x1, f3( x1,x2 ) ] }. (1.1)
описывает суперпозицию функций f1, f2 и f3.
Формулы, входящие в основную формулу, называются подформулами. Обычно формулы, как правило, имеют более привычный вид, при котором знаки логических операций стоят между переменными. Такая запись формулы называется инфиксной.
Например, пусть f1 –дизъюнкция, f2 – конъюнкция, а f3 – сложение по mod 2. Тогда формула (1.1) в инфиксной записи будет иметь вид:
F
= ( x3![]() x1
)
x1
)
![]() (
x1 & ( x1
x2
) ).
(1.2)
(
x1 & ( x1
x2
) ).
(1.2)
Любая формула задает способ ее вычисления, если известно, как вычислить вхо-дящие в нее функции.
Пример. Вычислить значение выражения (1.2) при х1 = х2 = 1, х3 = 0.
Вычисления будем производить в следующем порядке:
х3 х1 = 0 1 = 1 , x1 x2 = 1 1 = 0,
x1 & ( x1 x2 ) = 1 & 0 = 0, F = 1 0 = 1.
Таким образом, формула каждому набору значений переменных ставит в соответствие значение функции и, следовательно, может служить способом задания и вычисления логической функции.
Конъюнкция
|
Дизъюнкция
|
Сложение по модулю 2
|
Штрих Шеффера
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Импликация
|
Отрицание
|
Эквиваленция
|
Стрелка Пирса
|
27. Запись может быть префиксной — знак операции стоит перед операндами (польская запись), инфиксной — знак операции стоит между операндами или постфиксной — знак операции стоит после операндов. При числе операндов более 2-х префиксная и постфиксная записи экономичнее.
Определение. Эквивалентными (равносильными) называются формулы, представляющие одну и ту же функцию.
Эквивалентными формулами будут формулы в выражениях (1.3). В отличие от
табличного задания функции представление функции формулой не единственно.
Например, функцию Шеффера, функцию стрелка Пирса и можно представить следующими эквивалентными формулами:
х1 / x2 ~ ![]()
![]() ~
~
![]() ,
,
x1 “ x2 ~ ![]() &
&
![]() ~
~
![]() ,
(1.3)
,
(1.3)
Справедливость этих формул доказывает табл.1.11.
Таблица 1.11
x1 |
x2 |
х1/x2 |
|
|
|
x1x2 |
|
x1“x2 |
|
x1 x2 |
|
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
28. Свойства логических операций
Коммутативность: x
 y
= y
x,
y
= y
x,
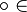 {&,
{&,
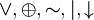 }.
}.Идемпотентность: x x = x, {&, }.
Ассоциативность: (x y) z = x (y z), {&,
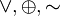 }.
}.Дистрибутивность конъюнкций и дизъюнкции относительно дизъюнкции, конъюнкции и суммы по модулю два соответственно:
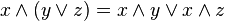 ,
,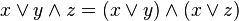 ,
,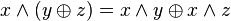 .
.
Законы де Мо́ргана:
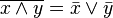 ,
,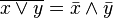 .
.
Законы поглощения:
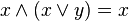 ,
,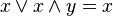 .
.
Другие (1):
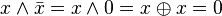 .
.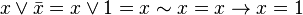 .
.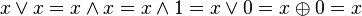 .
.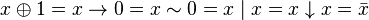 .
., инволютивность отрицания, закон снятия двойного отрицания.
Другие (2):
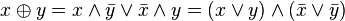 .
.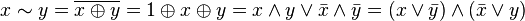
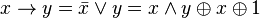 .
.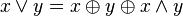 .
.
Другие (3) (Дополнение законов де Мо́ргана):
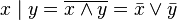 .
.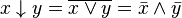 .
.
Закон исключённого
третьего
![]()
Закон противоречия
![]()
29. Система функций алгебры логики называется функционально полной, если любая функция от произвольного числа аргументов n может быть представлена с помощью этих функций. Полная система функций называется базисом. Минимальным базисом называется такой базис, для которого удаление хотя бы одной из функций, образующих этот базис, превращает систему функций в неполную. Так, полная система из дизъюнкции, конъюнкции и инверсии может быть сокращена, поскольку с помощью формул де Моргана можно представить либо конъюнкцию через инверсию и дизъюнкцию, либо дизъюнкцию через инверсию и конъюнкцию. Таким образом, базис из дизъюнкции, конъюнкции и инверсии не является минимальным. Поскольку ни дизъюнкция, ни конъюнкция не могут быть выражены через инверсию и наоборот, то базисы, состоящие из инверсии и дизъюнкции и из инверсии и конъюнкции, являются минимальными.
>Возможны различные базисы и минимальные базисы, отличающиеся числом входящих в них функций и их видом. Приведем примеры функционально полных систем:
конъюнкция, дизъюнкция, инверсия;
конъюнкция, инверсия;
дизъюнкция, инверсия;
стрелка Пирса;
штрих Шеффера.
Булевой алгеброй[1][2][3] называется непустое множество A с двумя бинарными операциями (аналог конъюнкции), (аналог дизъюнкции), унарной операцией (аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для всех a, b и c из множества A верны следующие аксиомы:
|
|
ассоциативность |
|
|
коммутативность |
|
|
законы поглощения |
|
|
дистрибутивность |
|
|
дополнительность |
Самая простая нетривиальная булева алгебра содержит всего два элемента, 0 и 1, а действия в ней определяются следующей таблицей:
|
|
|
|
|
|
|
|
31. В булевых алгебрах существуют двойственные утверждения, они либо одновременно верны, либо одновременно неверны. Именно, если в формуле, которая верна в некоторой булевой алгебре, поменять все конъюнкции на дизъюнкции, 0 на 1, ≤ на ≥ и наоборот, то получится формула, также истинная в этой булевой алгебре. Это следует из симметричности аксиом относительно таких замен.
В этом состоит принцип двойственности, который в общем виде записывается так:
![]() ,
,
![]() .
.
Для любого числа переменных это правило, называемое еще теоремой де Моргана, имеет вид:
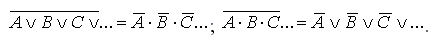 .
.
На практике принцип двойственности приводит к тому, что логический элемент, выполняющий в положительной логике операцию И, в случае отрицательной логики будет выполнять операцию ИЛИ.
32. Дизъюнктивная нормальная форма (ДНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любая булева формула может быть приведена к ДНФ.[1] Для этого можно использовать закон двойного отрицания, закон де Моргана, закон дистрибутивности. Дизъюнктивная нормальная форма удобна для автоматического доказательства теорем.
