32. Смешанное произведение векторов в координатах.

 Если      то

33. Условия коллинеарности, ортогональности, компланарности векторов.

Коллинеарные векторы – векторы, у которых задающие их отрезки параллельны одной и той же прямой.

Примечание: если из двух коллинеарных векторов направление одинаковое, то вектора сонаправленные, а если противоположные, то называется противоположно-направленные.

Компланарные векторы – векторы, у которых задающие их отрезки параллельны одной и той же плоскости.

Примечание: два вектора в пространстве всегда компланарны.

Примечание: два вектора называются равными, если они сонаправлены и равны по длине.

34. Нормальное уравнение плоскости.

35. Общее уравнение плоскости. Частные случаи расположения плоскости.

Ax+By+Cz+D=0

Данное уравнение определяет систему координат Оxyz на плоскость.

Частные случаи расположения плоскости определяемое общем уравнением.

• А=0 плоскость параллельна Ох

• B=0 плоскость параллельна Оy

• C=0 плоскость параллельна Оz

• D=0 через начало координат

• A=B=0 Перпендикулярно Oz (параллельно xOy)

• A=C=0 Перпендикулярно Oy (параллельно xOz)

• B=C=0 Перпендикулярно Ox (параллельно yOz)

• A=D=0 Проходит через ось Ox

• B=D=0 Проходит через ось Oy

• C=D=0 Проходит через осьOz

• A=B=D=0 Совпадает с плоскостью xOy

• A=C=D=0 Совпадает с плоскостью xOz

• B=C=D=0 Совпадает с плоскостью yOz

36. Уравнение плоскости в отрезках

. ,            

37. Уравнение плоскости, проходящее через заданную точку.

Точка Мо(Хо, Уо), вектор

Уравнение плоскости, проходящей через 3 точки.

38. Угол между плоскостями. Условие параллельности и перпендикулярности.

Условие перпендикулярности

условие параллельности

39. Расстояние от точки до плоскости.

40. Общее уравнение прямой в R³

Общие уравнения прямой:

А₁х +B₁y + C₁z + D₁=0

A₂x + B₂y + C₂z + D₂=0

41. векторное уравнение прямой.

42. Параметрическое и каноническое уравнение прямой.

Канонические уравнения прямой линии в пространстве, или уравнения прямой с направляющими коэффициентами, имеют вид:

.

где x0, y0, z0 - координаты точки, через которую проходит прямая, а m, n и p - направляющие коэффициенты прямой, которые являются проекциями на координатные оси Ox, Oy, Oz направляющего вектора прямой.

В параметрическом виде уравнения прямой линии в пространстве записываются так:

.

43. Уравнение прямой, проходящей через 2 заданные точки.

44. Приведение общего уравнения прямой к каноническому виду.

45. Угол между прямыми. Условие параллельности и перпендикулярности прямой.

Услов. параллельности: А₁ / А₂ = В₁ / В₂

Услов. Перпендикулярности : А₁А₂ + В₁В₂ = 0

46. Прямая линия на плоскости. Нормальное уравнение прямой

Cosα,Cosβ- направляющие косинусы нормального вектора n.

p- расстояние от начала координат до прямой.

47. Общее уравнение прямой. Исследование общего уравнения прямой.

Ах + Ву + С = 0,

причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи:

•  C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат

•  А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох

•  В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу

•  В = С = 0, А ≠0 – прямая совпадает с осью Оу

•  А = С = 0, В ≠0 – прямая совпадает с осью Ох

48. Уравнение прямой, проходящей через данную точку в данном направлении.

k-угловой коэффициент

49. Уравнение прямой проходящие через 2 заданные точки R².

Пусть в пространстве заданы две точки M ₁ ( x ₁ , y ₁ , z ₁ ) и M₂ ( x ₂, y ₂ , z ₂ ), тогда уравнение прямой, проходящей через эти точки:

50. Угол между прямымиR².

Если заданы две прямые y = k₁ x + b₁ , y = k ₂x + b₂ , то острый угол между этими прямыми будет определяться как .

51. Условие параллельности и перпендикулярности прямыхR².

Условие параллельности 2 прямых записывается в виде ││ , =

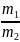
Условие перепендикулярности прямых записывается в ( , )= 0

52. Уравнение прямой в отрезках

53. Расстояние от точки до прямой в К. Угол между 2 прямыми. Условия параллельности и перпендикулярности. Уравнение прямой с угловым коэффициентом. Уравнение прямой в отрезках.

Расстояние от точки до прямой:  расстояние от точки   до точки  на плоскости находится через координаты точек по формуле  угол между ними определяется по формуле Если прямая задана общим уравнением ,то ее угловой коэффициент определяется по формуле . Если прямая проходит через точки  ( ,  ),  ( ,  ), то ее угловой коэффициент определяется по формуле . Если известны угловые коэффициенты   и   двух прямых, то один из углов   между этими прямыми определяется по формуле . Признаком параллельности двух прямых является равенство их угловых коэффициентов: . Признаком перпендикулярности двух прямых является соотношение , или  .