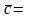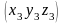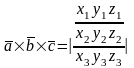- •Матрицы. Основные понятия. Линейные операции над матрицами и их свойства.
- •Определитель матрицы. Свойства определителей.
- •Миноры и алгебраические дополнения.
- •Теорема замещения.
- •Теорема аннулирования.
- •Некоторые методы вычисления определителей.
- •Умножение матриц. Свойства умножения.
- •Транспонирование матриц.
- •Обратная матрица. Необходимое и достаточное условие существования обратной матрицы. Нахождение обратной матрицы.
- •Матричная запись системы линейных уравнений и её решения.
- •Решение невырожденных линейных систем, формулы Крамера.
- •Ранг матрицы. Свойства ранга матрицы. Вычисление ранга матрицы с помощью элементарных преобразований.
- •Теорема Кронекера - Капелле. Решение произвольных линейных систем.
- •Система однородных линейных уравнений.
- •Решение систем линейных уравнений методом последовательного исключения неизвестных (метод Гаусса).
- •Размерность и базис линейного пространства.
- •Вектор. Проекция вектора на ось.
- •Теорема об единственности разложения вектора по базису. Координаты вектора. Декартова система координат.
- •Расстояние между двумя точками.
- •Деление отрезка в данном отношении.
- •Направление вектора в пространстве.
- •Скалярное произведение векторов и его свойства.
- •Механический смысл скалярного произведения.
- •Ортонормированный базис. Выражение скалярного произведения через координаты в ортонормированном базисе.
- •Векторное произведение векторов и его свойства.
- •Смешанное произведение векторов в координатах.
- •Условия коллинеарности, ортогональности, компланарности векторов.
- •Нормальное уравнение плоскости.
- •Общее уравнение плоскости. Частные случаи расположения плоскости.
- •Угол между прямой и плоскостью. Условие параллельности и перпендикулярности прямой и плоскости. Определение точек пересечения прямой и плоскости.
- •Окружность. Определение. Вывод канонического уравнения.
- •Эллипс. Определение. Вывод канонического уравнения. Исследование формыэллипса.
- •Гипербола. Определение. Вывод канонического уравнения гиперболы. Исследование формы гиперболы.
- •Парабола. Определение. Вывод канонического уравнение параболы.
- •Исследование общего уравнения линии 2 порядка в случае отсутствия члена с произведением текущих координат.
- •Сфера. Определение. Вывод канонического уравнения.
- •Цилиндрические поверхности.
- •Эллипсоиды.
- •Гиперболоиды.
- •Параболоиды.
- •Канонические поверхности.
- •Функция. Основные понятия. Способы её задания.
- •Числовая последовательность и её предел.
- •Последовательность. Теорема Больцано – Вейерштрасса.
- •Число е. Натуральные логарифмы.
- •Конечный предел функции.
- •Бесконечный предел функции.
- •Односторонние пределы.
- •Бесконечно малые и бесконечно большие функции. Связь между б.М и б.Б функциями.
- •Предел суммы, произведения, частного.
- •Теорема о промежуточной функции
- •Первый замечательны предел.
- •Второй замечательный предел.
- •Сравнение б.М функций. Эквивалентные б.М функции.
- •Свойства эквивалентные б.М функций.
- •Непрерывность функции в точке. Определение. Свойства функций, непрерывных в точке.
- •Непрерывность функции на отрезке.
- •Свойства функций, непрерывных в отрезке. Точки разрыва и их классификация.
- •Производная. Определение. Механический и геометрический смысл производной.
- •Дифференцируемость функции. Определение. Теорема о непрерывности дифференцируемой функции.
- •Основные правила дифференцируемости.
- •Производная сложной функции.
- •Производная обратной функции.
- •Гиперболические функции и их дифференцирование.
- •Дифференцирование функций, заданной неявно.
- •Дифференцирование функций, заданной параметрически.
- •Производные и дифференциалы высших порядков.
- •Теорема Ролля. Геометрический смысл теоремы Ролля.
- •Теорема Лагранжа. Геометрический смысл теоремы Лагранжа.
- •Теорема Коши
- •Правило Лопиталя и его применение к вычислению переводов.
- •Формула Тейлора и её приложение.
- •1Исследование ф-ций и построение их графиков с помощью дифференциального исчисления.
Расстояние между двумя точками.
Расстояние d между
точками A(x1, y1)
и B(x2, y2)
плоскости определяется по формуле:
![]()
![]()
![]()
Деление отрезка в данном отношении.
Если x1 и y1 -
координаты точки A,
а x2 и y2 -
координаты точки B,
то координаты x и y точки C,
делящей отрезок AB в
отношении ![]()
![]()
![]() ,
определяются по формулам
,
определяются по формулам![]() Если
Если ![]()
![]() ,
то точка C(x, y)
делит отрезок AB пополам,
и тогда координаты x и y середины
отрезка AB определяются
по формулам
,
то точка C(x, y)
делит отрезок AB пополам,
и тогда координаты x и y середины
отрезка AB определяются
по формулам![]()
![]()
![]() ;
;
![]()
![]()
![]()
![]()
Направление вектора в пространстве.
Вектором называется упорядоченная пара точек. Первая точка называется началом вектора, вторая — концом вектора. Расстояние между началом и концом вектора называется его длиной. Вектор, начало и конец которого совпадают, называется нулевым, его длина равна нулю.Если длина вектора положительна, то его называют ненулевым.Ненулевой вектор можно определить также как направленный отрезок, т.е. отрезок, у которого одна из ограничивающих его точек считается первой (началом вектора), а другая — второй (концом вектора). Направление нулевого вектора, естественно, не определено.
Скалярное произведение векторов и его свойства.
Скалярное
произведение векторов
- число = произвед длин на косинус между
ними.
Скалярное произ 2х векторов
= модулю одного умноженного на проекцию
другого на соноправленную с 1-ым вектором
ось.
Свойства:
1.
a*b=b*a
2.
(C*a)*b=C*(a*b)
3.
a(b+c)=a*c+b*c;
4.
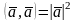 5.
(a,
b)
= 0 =>
5.
(a,
b)
= 0 =>
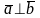 6.
ij
= jk
= kj
= 0.
Теорема
1: в пространстве R3
в ортонормированном базисе
6.
ij
= jk
= kj
= 0.
Теорема
1: в пространстве R3
в ортонормированном базисе
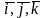 :
:
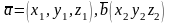
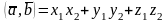 Следствие
из Т1:
Следствие
из Т1:
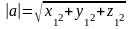 Для
вектора
Для
вектора
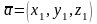 :
:
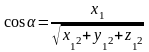 Механический
смысл скалярного произведения:
Пусть
Механический
смысл скалярного произведения:
Пусть
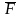 -
сила, которая перемещает тело в
направлении вектора S
( на длину
-
сила, которая перемещает тело в
направлении вектора S
( на длину
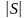 )
=>
)
=>
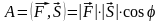
Механический смысл скалярного произведения.
Физический смысл: если матер. точка проходит путь S под действием силы F, то работа совершаемая при этом равна: A = FS = FScos
Ортонормированный базис. Выражение скалярного произведения через координаты в ортонормированном базисе.
Базис называется ортонормированным, если базисные векторы попарно ортогональны и длина каждого из них =1. Декартова система координат с ортонормированным базисом i,j,k называется прямоугольной системой координат, а векторы i,j,k ортами координатных осей. AB=xi+yi+ji
Векторное произведение векторов и его свойства.
Три некомпланарных вектора a, b, с взяты в указанном порядке и образуют правую тройку, если с конца 3-его вектора с кратчайший поворот от 1-ого a ко 2-ому b видим совершающийся против часовой стрелки, и левую – если по часовой.
Векторное произведение вектора a на b - это c, который:
1)с перпендикулярно a и b;
2)имеет длину, численно равную площади параллельного, параллелограмма на векторах |c|=|a|*|b|*sinσ; 3) векторы a, b, с образ правую тройку.
Замечание: Из определения вытекает след соотношения между ортами ijk:
1. i*j=k;
2. j*k=i;
3. k*i=j;
Свойства:
1)векторное
произ при перестановке множителей
меняет знак. (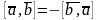 )
)
2)два ненулевых вектора коллинеарны, когда их векторное произв =0.
Пункты: 1)условие коллиниарности: a//b => a*b=0;
2)нахождение
S
параллелограмма и S
треуг. Sпар=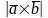 sin
sin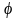 .
Sтр=0,5*
.
Sтр=0,5*
3)определение момента силы. |M|=|F|*|S|.
Теорема:
,
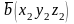
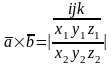
Механический смысл векторного произведения.
Механический смысл скалярного произведения векторов. Скалярное произведение силы F на вектор перемещения S равно работе А этой силы при перемещении материальной точки по вектору S: A = FS
Векторное произведение в координатах.
Векторное
произведение в координатах
Если ![]()
![]() ,
то
,
то ![]() или
или ![]() или
или ![]()
![]()
Приложение векторного произведения в геометрии и механике.
1)коллинеарность условие: ax/bx=ay/by=az/bz
2)Если F приложена к точке А то вращательный момент силы под действием
которой А вращается вокруг неподвижной точки О: М=ОАxА =ОАFsin
3)линейная скорость: V = w x r.
Смешанное произведение, геометрический смысл. Свойства смешанного произведения.
Смешанное произведение 3х векторов равно объёму параллелепипеда, построенного на этих векторах, взятого со знаком + (-), если эти векторы образуют правую (левую) тройку.
Свойства:
1)смешанное произв не меняется при циклической перестановке его множителей.
( .
.
2)смешанное произв меняет знак при перемене мест любых букв любых сомножителей
3)смешанное произ ненулевых векторов =0 тога, когда они компланарны.
Смешанное
произ векторов
= определителю 3-его порядка, составленного
из координат перемноженных векторов.
Приложение. 1)определение взаимных
ориентаций векторов в пространстве:
если
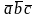 >0
(
<0),
то правая (левая) тройка векторов
2)комплонарность
векторов:
компланарны,
когда их произв =0.
3)Геометрический
смысл: Vпараллелепипеда=
.
Vтр=1/6(
).
Вычисление:
,
>0
(
<0),
то правая (левая) тройка векторов
2)комплонарность
векторов:
компланарны,
когда их произв =0.
3)Геометрический
смысл: Vпараллелепипеда=
.
Vтр=1/6(
).
Вычисление:
,