13. Теорема Кронекера - Капелле. Решение произвольных линейных систем.

Теорема Кронекера-Капелли: система лин алг ур-ий совместна, когда rangA=rang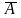 (волнистая). Теорема: если rang совместной системы= числу неизвестных, то система имеет одно решение. Теорема: если ранг совмест сист < числа неизвестных, то система имеет бесконеч решений.

Правило решения СУ.

1)найти ранг основной и расширенной матрицы (если rA не =rA с крыш, то система несовместна.

2) если rA=rA с крыш и =r, то система совместна и надо найти базисный минор порядка r.

3)Берём r ур-ий из коэф которых составлен базисн минор. Остальные ур-ия отбрасываем. Неизвестные, коэф которых входят в минор наз главными. Из оставл слева, а остальные (n-r) – справа.

4)Найти выражения главных неизв через свободные. Получено общее решение системы

5)Придавая свободным низвестным произвольное значение, получим соотв значения главн неизв, т.е. найдём частные решения.

14. Система однородных линейных уравнений.

АХ=В – система и параллельно рассмотрим систему АХ=0. (АХ=В – Неоднородн. СЛАУ, АХ=0 – однородн. СДАУ).

Одновременно выполняется:

1. АХ=0 имеет тольок тривиальное решение, АХ=В имеет единственное решение или не имеет решений совсем.

2. АХ=0 имеет нетривиальное решение, АХ=В имеет бесконечное число решений.

Рассмотрим подробнее 2-ой случай: r(A) = r(A с волной сверху)<m..

M – r(A) – дефект, количество свободных неизвестных.

Пример: ,

б.м: х₁, х₂

св.м: х₃, х₄.

х₂ + х₃ +2х₄ = 1., х₂ = 1 – а – 2b, х₃ = а, х₄ = b.

х₁ = -2х₂ – х₃ + х₄ + 1 = -2 + 2а +4b – а + b+1 = -1 + а + 5b.

Ответ: (-1 + а + 5b., 1 – а – 2b , а, b)^Т.

15. Решение систем линейных уравнений методом последовательного исключения неизвестных (метод Гаусса).

Метод Гаусса для решения системы линейных уравнений

1. Выражаем первое неизвестное из первого уравнения и подставляем его в остальные уравнения.

2. Получаем новую систему, в которой число уравнений и неизвестных на 1 меньше.

3. С новой системой поступаем таким же образом и так продолжаем до тех пор, пока не останется одно линейное уравнение, которое легко решается.

4. Когда получено значение последнего неизвестного x_n, подставляем его в уравнение, которое позволяет найти x_n – 1 по x_n.

5. По найденным x_n – 1 и x_n находим x_n – 2 и таким образом находим последовательно все неизвестные.

16. Размерность и базис линейного пространства.

Пусть система n векторов линейно-независима, а любая система n+1 векторов – линейно зависима, тогда число n называют размерностью пространства. dimV=n

Система этих n линейно-независимых векторов называется базисом линейного пространства. Рассмотрим систему n+1 векторов. Такое представление называется разложение по базису, а числа называют координатами вектора.