9. Обратная матрица. Необходимое и достаточное условие существования обратной матрицы. Нахождение обратной матрицы.

Пусть есть матрица А – невырожденная.

А^-1, A^-1*A=A*A^-1=E, где E –единичная матрица. A^-1 имеет те же размеры, что и A.

Алгоритм нахождения обратной матрицы:

1. вместо каждого элемента матрицы а_ij записываем его алгебраическое дополнение.

а_ij А_ij

А* - союзная матрица.

2. транспонируем полученную союзную матрицу. А^*Т

3. делим каждый элемент союзной матрицы на определитель матрицы А.

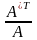, A^-1 = A^*Т

Теорема: (об аннулировании определителя): сумма произведений элементов некоторого ряда определителя на алгебраическое дополнение к элементам другого параллельного ряда всегда равна нулю.

10. Матричная запись системы линейных уравнений и её решения.

Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:

Рассмотрим матрицу системы   и матрицы столбцы неизвестных и свободных членов 

Найдем произведение

т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде

 или короче A∙X=B.

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.

Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A^-1, обратную матрице A:  . Поскольку A^-1A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A^-1B.

Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A^-1B.

11. Решение невырожденных линейных систем, формулы Крамера.

СЛАУ принято записывать в матричной форме, когда сами неизвестные не указываются, а указывается только матрица системы А и столбец свободных членов В.

Решение невырожденных СЛАУ методом Крамера:

Х=А^-1*В

А^-1=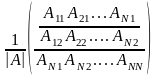

X1= (A₁₁b₁ + A₂₁b₂ + …+A_n1b_n)

Теорема: (Крамера): решение невырожденных уравнений АХ=В, можно записать так:

, Ак получается из А путем замены к-го столбца на столбец свободного члена В.

12. Ранг матрицы. Свойства ранга матрицы. Вычисление ранга матрицы с помощью элементарных преобразований.

Максимальное число линейно-зависимых строк матрицы A наз. рангом матрицы и обознач r(a). Наибольшее из порядков миноров данной матрицы отличных от 0 наз рангом матрицы.

Свойства:

1)при транспонировании rang=const.

2)если вычеркнуть нулевой ряд, то rang=const;

3)rang=cost, при элементарных преобразованиях.

3)для вычисл ранга с помощью элементар преобраз матрица A преобраз в матриц B, ранг которой легко находится.

4)ранг треуг матрицы=числу ненулевых элем, располож на глав. диагоналях.

Методы нахождения ранга матрицы:

1. метод окаймляющих миноров

2. метод элементарных преобразований

Метод окаймляющих миноров:

метод окаймляющих миноров позволяет алгоритмизировать процесс нахождения ранг-матрицы и позволяет свести к минимуму количество вычисления миноров.

1. если в матрице все нулевые элементы, то ранг = 0

2. если есть хоть один ненулевой элемент => r(a)>0

теперь будем окаймлять минор М1, т.е. будем строить всевозможные миноры 2-ого порядка, ктр. содержат в себе i-тую строку и j-тый столбец, до тех пор, пока не найдем ненулевой минор 2-ого порядка.

М2 (i, i1, j.j1)

Дальше аналогично строим миноры 3-го порядка, окаймляющие М2 (минор), до тех пор, пока не получим минор, отличный от нуля.

Процесс будет продолжаться до одного из событий: 1. размер минора достигнет числа к.

2. на каком-то этапе все окаймленные миноры окажутся = 0.

В обоих случаях величина ранга-матрицы будет равна порядку большего отличного от нуля минора.

Метод элементарных преобразований: как известно, понятие треугольной матрицы определяется только для квадратных матриц. Для прямоугольных матриц аналогом является понятие трапецивидной матрицы.

Например: ранг = 2.