
- •Матрицы. Основные понятия. Линейные операции над матрицами и их свойства.
- •Определитель матрицы. Свойства определителей.
- •Миноры и алгебраические дополнения.
- •Теорема замещения.
- •Теорема аннулирования.
- •Некоторые методы вычисления определителей.
- •Умножение матриц. Свойства умножения.
- •Транспонирование матриц.
- •Обратная матрица. Необходимое и достаточное условие существования обратной матрицы. Нахождение обратной матрицы.
- •Матричная запись системы линейных уравнений и её решения.
- •Решение невырожденных линейных систем, формулы Крамера.
- •Ранг матрицы. Свойства ранга матрицы. Вычисление ранга матрицы с помощью элементарных преобразований.
- •Теорема Кронекера - Капелле. Решение произвольных линейных систем.
- •Система однородных линейных уравнений.
- •Решение систем линейных уравнений методом последовательного исключения неизвестных (метод Гаусса).
- •Размерность и базис линейного пространства.
- •Вектор. Проекция вектора на ось.
- •Теорема об единственности разложения вектора по базису. Координаты вектора. Декартова система координат.
- •Расстояние между двумя точками.
- •Деление отрезка в данном отношении.
- •Направление вектора в пространстве.
- •Скалярное произведение векторов и его свойства.
- •Механический смысл скалярного произведения.
- •Ортонормированный базис. Выражение скалярного произведения через координаты в ортонормированном базисе.
- •Векторное произведение векторов и его свойства.
- •Смешанное произведение векторов в координатах.
- •Условия коллинеарности, ортогональности, компланарности векторов.
- •Нормальное уравнение плоскости.
- •Общее уравнение плоскости. Частные случаи расположения плоскости.
- •Угол между прямой и плоскостью. Условие параллельности и перпендикулярности прямой и плоскости. Определение точек пересечения прямой и плоскости.
- •Окружность. Определение. Вывод канонического уравнения.
- •Эллипс. Определение. Вывод канонического уравнения. Исследование формыэллипса.
- •Гипербола. Определение. Вывод канонического уравнения гиперболы. Исследование формы гиперболы.
- •Парабола. Определение. Вывод канонического уравнение параболы.
- •Исследование общего уравнения линии 2 порядка в случае отсутствия члена с произведением текущих координат.
- •Сфера. Определение. Вывод канонического уравнения.
- •Цилиндрические поверхности.
- •Эллипсоиды.
- •Гиперболоиды.
- •Параболоиды.
- •Канонические поверхности.
- •Функция. Основные понятия. Способы её задания.
- •Числовая последовательность и её предел.
- •Последовательность. Теорема Больцано – Вейерштрасса.
- •Число е. Натуральные логарифмы.
- •Конечный предел функции.
- •Бесконечный предел функции.
- •Односторонние пределы.
- •Бесконечно малые и бесконечно большие функции. Связь между б.М и б.Б функциями.
- •Предел суммы, произведения, частного.
- •Теорема о промежуточной функции
- •Первый замечательны предел.
- •Второй замечательный предел.
- •Сравнение б.М функций. Эквивалентные б.М функции.
- •Свойства эквивалентные б.М функций.
- •Непрерывность функции в точке. Определение. Свойства функций, непрерывных в точке.
- •Непрерывность функции на отрезке.
- •Свойства функций, непрерывных в отрезке. Точки разрыва и их классификация.
- •Производная. Определение. Механический и геометрический смысл производной.
- •Дифференцируемость функции. Определение. Теорема о непрерывности дифференцируемой функции.
- •Основные правила дифференцируемости.
- •Производная сложной функции.
- •Производная обратной функции.
- •Гиперболические функции и их дифференцирование.
- •Дифференцирование функций, заданной неявно.
- •Дифференцирование функций, заданной параметрически.
- •Производные и дифференциалы высших порядков.
- •Теорема Ролля. Геометрический смысл теоремы Ролля.
- •Теорема Лагранжа. Геометрический смысл теоремы Лагранжа.
- •Теорема Коши
- •Правило Лопиталя и его применение к вычислению переводов.
- •Формула Тейлора и её приложение.
- •1Исследование ф-ций и построение их графиков с помощью дифференциального исчисления.
1Исследование ф-ций и построение их графиков с помощью дифференциального исчисления.
а)убывание\возрастание ф-ции на интервале АВ
б)экстремум ф-ции(необходимое условие существования экстремума)
Теорема
(необходимое условие экстремума).
Если дифференцируемая функция y=f(x)
имеет экстремум в точке
,
то ее производная в этой точке равна
нулю:
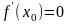 .
Док-во:
Пусть, для определенности,
-точка
максимума. Значит, в окрестности точки
выполняется неравенство
.
Док-во:
Пусть, для определенности,
-точка
максимума. Значит, в окрестности точки
выполняется неравенство
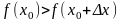 .
Но тогда
.
Но тогда
 ,
если
,
если
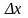 >0,
и
>0,
и
 ,
если
<0.
По условию теоремы производная
,
если
<0.
По условию теоремы производная
 существует. Переходя к пределу, при
существует. Переходя к пределу, при
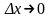 ,
получим
,
получим
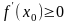 ,
если
<0
и
,
если
<0
и
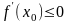 ,
если
>0.
Поэтому :
.
,
если
>0.
Поэтому :
.
в) достаточное условие для существования экстремума
Теорема
(достаточное условие экстремума): Если
непрерывная функция f(x)
дифференцируема в некоторой
-окрестности
и критической точки
и при переходе через нее 9слева направо)
производная
меняет
знак с плюса на минус, то
есть точка максимума; с минуса на плюс,
то
-точка
минимума. Док-во:
рассмотрим
-окрестность
точки
.
Пусть выполняются условия:
 и
.
Тогда функция f(x)
возрастает на интервале
и
.
Тогда функция f(x)
возрастает на интервале
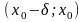 ,
а на интервале
,
а на интервале
 она убывает. Отсюда следует, что значение
f(x)
в точке
является наибольшим на интервале
она убывает. Отсюда следует, что значение
f(x)
в точке
является наибольшим на интервале
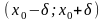 ,
т.е. f(x)<f(
)
для всех
,
т.е. f(x)<f(
)
для всех
 .
Это и означает, что
- точка максимума функции.
.
Это и означает, что
- точка максимума функции.
г)точки перегиба графика ф-ции (необходимое и достаочное условия) существования точек перегиба)
Достаточное
условие точки перегиба:
Пусть f
- дважды дифференцируемая функция в
окрестности
и
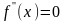 или
или
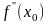 не
существует. Если при этом для любых
не
существует. Если при этом для любых
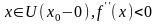 ,
а для любых
,
а для любых
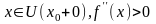 ,
то
- точка перегиба.
,
то
- точка перегиба.
д) асимптоты графика: вертикальные, наклонные и горизонтальные
е) Общая схема исследования ф-ции и построения графика. Наибольшее и наименьшее значение ф-ции на отрезке
Общая
схема исследования функции.
1. Находим область определения D(x).
2. Находим точки разрыва второго род,
обозначаем вертикальные асимптоты. 3.
Исследуем функцию на четность/нечетность,
периодичность. 4. Находим точки пересечения
с Ox
и Oy.
С Ox:
x=o,
y-?.
C
Oy:
y=0,
x-?
5. Находим наклонные асимптоты, если
они есть. 6. Исследуем функцию на наличие
критических точек. Решаем уравнение
 .
7. Определяем промежутки монотонности.
8. Находим вторую производную и точки,
для которых она равна 0 или не существует.
9. Находим промежутки знакопостоянства
второй производной. 10. Составляем
таблицу. 11. на основе таблицы определяем
точки локального экстремума и точки
перегиба.
.
7. Определяем промежутки монотонности.
8. Находим вторую производную и точки,
для которых она равна 0 или не существует.
9. Находим промежутки знакопостоянства
второй производной. 10. Составляем
таблицу. 11. на основе таблицы определяем
точки локального экстремума и точки
перегиба.
