103. Производные и дифференциалы высших порядков.

Пусть существует такое множество X, что для  . Тогда может получиться, что производная   имеет производную в некотрой точке. Такая производная называется второй производной или производной второго порядка. Обозначается   или  . В общем виде  . Переходя к дифференциалам, получаем:  .   .

Не следует путать обозначения:  ,  . Второй дифференциал от x равен 0 только тогда, когда x - независимая переменная или линейная функция от независимой переменной. В этом случае любой дифференциал  . То есть для  дифференциалы высших порядков.

104. Теорема Ролля. Геометрический смысл теоремы Ролля.

Если функция f(x) непрерывна на отрезке [a,b], дифференцируема на интервале (a,b) и на концах отрезка принимает одинаковые значения f(a)=f(b), то найдется хотя бы одна точка 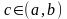, в которой производная 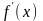обращается в ноль, т.е. .

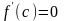105. Теорема Лагранжа. Геометрический смысл теоремы Лагранжа.

Теорема Лагранжа: Если функция f(x) непрерывна на отрезке [a,b], дифференцируема на интервале (a,b), то найдется хотя бы одна точка такая, что выполняется равенство 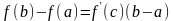. Это так же является формулой о конечном приращении: приращение дифференцируемой функции на отрезке [a,b] равно приращению аргумента, умноженному на значение производной функции в некоторой точке этого отрезка. Если производная функции равна нулю на некотором промежутке, то функция постоянна на этом промежутке. Если две функции имеют равные производные на некотором промежутке, то они отличаются друг от друга на постоянное слагаемое.

106. Теорема Коши

Теорема Коши: Если функции f(x) и 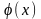непрерывны на отрезке [a,b], дифференцируемы на интервале (a,b), причем 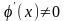для 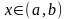, то найдется хотя бы одна точка , такая, что выполняется равенство .

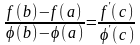107. Правило Лопиталя и его применение к вычислению переводов.

Правило Лопиталя (по раскрытию неопределенностей вида 0/0) : Пусть функции f(x) и непрерывны и дифференцируемы в окрестности точки 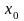и обращаются в ноль в этой точке: f( )=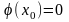 . Пусть в окрестности точки . Если существует предел 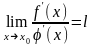, то .

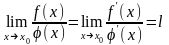Правило Лопиталя (по раскрытию неопределенностей вида 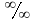) : Пусть функции f(x) и непрерывны и дифференцируемы в окрестности точки (кроме, может быть, точки ), в этой окрестности 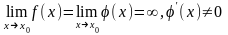. Если существует предел .

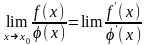108. Формула Тейлора и её приложение.

 изображающая функцию f (x), имеющую n-ю производную f ⁽ⁿ⁾(a) в точке х = а, в виде суммы многочлена степени n, расположенного по степеням х—а, и остаточного члена R_n (x), являющегося в окрестности точки а бесконечно малой более высокого порядка, чем (x—a) ⁿ [то есть R_n (x) = an (x)(x—a) ⁿ, где an (x) → 0 при х → а]. Если в интервале между а и х существует (n + 1)-я производная, то R_n (x) можно представить в видах:

 где ξ и ξ₁ — какие-то точки указанного интервала (остаточный член Т. ф. в формах Лагранжа и соответственно Коши). График многочлена, входящего в Т. ф.. имеет в точке а Соприкосновение не ниже n-го порядка с графиком функции f (x). Т. ф. применяют для исследования функций и для приближённых вычислений.