93. Производная обратной функции.

Производная обратной функции: y = f(х) с областью определения Д и значений Е. Если обратное ей соответствие таково, что для каждого у є Е, определяется единственное значение х є Д, то мы получим обратную функцию. Обратная – х = f ^-1 (у)Пусть y = f(х) имеет в точке х_О производную f (x_O) = lim _{x 0} y / х. Чтобы найти производную обратной функции нужно найти предел lim _{x 0} х / у = (f ^-1 (y_O))Вследствие непрерывности функции y = f(х) при x0 у0, тогда lim _{x 0} х / у = 1 / f  (х_O).Производные обратных функций обратны по величине:

х  (у_O) = 1 / f  (х_O) f  (х_O)  0

у  (х_O) = 1 / f  (у_O) f  (у_O)  0

94. Производные основных элементарных функций: sinu, cosu, tgu, ctgu, uⁿ, a^u, e^u, lnu, logu, arcsinu, arcosu, arcctgu, гдеu = u(x).

Производные основных элементарных функций.

1)С = 0; 9)

2)(x^m) = mx^m-1; 10)

3) 11)

4) 12)

5) 13)

6) 14)

7) 15)

8) 16)

95. Гиперболические функции и их дифференцирование.

Гиперболические функции: Встречаются различные комбинации показательных функций. Их рассматривают как новые функции:

Гип. синус – Sh - (e^x – e^-x) /2

Гип. косинус - Ch – (e^x + e^-x) / 2

Гип. тангенс – th - (e^x – e^-x / 2) / (e^x + e^-x / 2)

Гип. котангенс – cth - (e^x + e^-x / 2) / (e^x – e^-x / 2)

(Sh x) = Ch x (Ch x) = - Sh x

(th x) = 1 / Ch² x (cth x) = - 1/ Sh² x

96. Дифференцирование функций, заданной неявно.

Пусть функция y f x = ( ) задана уравнением F x y ( , ) = 0 . В этом случае говорят, что функция задана неявно . Для нахождения производной считаем, что в уравнении y зависит от x ,иначе. Другими словами дифференцируем уравнение , считая сложной функцией, зависящей отF x y x , ( ) = 0 F x y x , ( ) = 0 y x .

97. Дифференцирование функций, заданной параметрически.

Пусть

Предположим, что эти функции имеют производные и функция x = (t) имеет обратную функцию t = Ф(х).

Тогда функция у = (t) может быть рассмотрена как сложная функция y = [Ф(х)].

т.к. Ф(х) – обратная функция, то

Окончательно получаем:

Таким образом, можно находить производную функции, не находя непосредственной зависимости у от х.

98. Дифференциал функции. Его связь с производной.

Дифференциал функции - это произведение производной  f ’( x₀ ) и приращения аргумента    : df = f ’( x₀ ) ·   .

99. Применение дифференциала в приближенных вычислениях.

Если приращение delt x аргумента мало по абсолютной величине,то delt y приблизительно равно dy и получаем формулу приближенных вычеслений с помошью дифферинциалов f (x_O +delt x) приблизительно равно f (x_O) + f `(x_O) delt x

100. Геометрический смысл дифференциала.

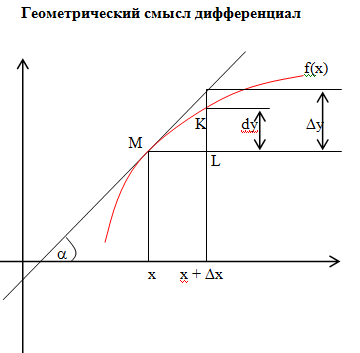Из треугольника MKL: KL = dy = tgx = yx

Таким образом, дифференциал функции f(x) в точке х равен приращению ординаты касательной к графику этой функции в рассматриваемой точке.

101. Основные правила и формулы нахождения дифференциала (таблица дифференциалов, дифференциал постоянной, суммы, произведения, частного).

Основные правила дифференцирования.

Обозначим f(x) = u, g(x) = v- функции, дифференцируемые в точке х.

1) (u  v) = u  v

2) (uv) = uv + uv

3) , если v  0

Эти правила могут быть легко доказаны на основе теорем о пределах.

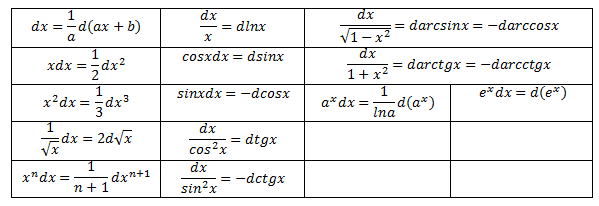
102. Инвариантность формы дифференциала первого порядка.

Инвариантная форма записи дифференциала.

Пусть y = f(x), x = g(t), т.е у- сложная функция.

Тогда dy = f(x)g(t)dt = f(x)dx.

Видно, что форма записи дифференциала dy не зависит от того, будет ли х независимой переменной или функцией какой- то другой переменной, в связи с чем эта форма записи называется инвариантной формой записи дифференциала.

Однако, если х- независимая переменная, тот dx = x, но если х зависит от t, то х  dx.

Таким образом форма записи dy = f(x)x не является инвариантной.