85. Свойства эквивалентные б.М функций.

Свойства эквивалентных бесконечно малых:

1. Разность двух эквивалентных бесконечно малых есть бесконечно малая высшего порядка относительно каждой из них.

2. Если из суммы нескольких бесконечно малых разных порядков отбросить бесконечно малые высших порядков, то оставшаяся часть, называемая главной, эквивалентна всей сумме.

Из первого свойства следует, что эквивалентные бесконечно малые могут сделаться приближенно равными со сколь угодно малой относительной погрешностью. Поэтому знак мы применяем как для обозначения эквивалентности бесконечно малых, так и для записи приближенного равенства их достаточно малых значений.

86. Непрерывность функции в точке. Определение. Свойства функций, непрерывных в точке.

Пусть функция f(x) определена в некоторой окрестности O(x0) точки x0 (включая саму точку x0).

Функция f(x) называется непрерывной в точке x0, если существует 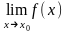, равный значению функции f(x) в этой точке: =f(x0). Необходимое и достаточное условие непрерывности функции в точке :

Функция y = f(x) непрерывна в точке х0 тогда и только тогда, когда

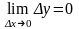
Замечание. Условие можно трактовать как второе определение непрерывности функции в точке. Оба определения эквивалентны.

Пусть функция f(x) определена в полуинтервале [x0, x0 + δ ).

Функция f(x) называется непрерывной справа в точке x0, если существует односторонний предел

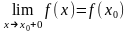
Пусть функция f(x) определена в полуинтервале (x0 − δ, x0].

Функция f(x) называется непрерывной слева в точке x0, если существует односторонний предел

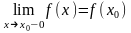
Непрерывность суммы, произведения и частного двух непрерывных функций :

Теорема 1. Если функции f(x) и g(x) непрерывны в точке х0, то в этой точке непрерывны

f(x) ± g(x),

f(x) · g(x),

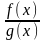, (g(x0) ≠ 0).

87. Непрерывность функции на отрезке.

1) Функция называется непрерывной справа в точке a, если lim _{x  a + 0} f(x) = f (a) и непрерывной слева в точке a, если lim _{x  b + 0} f(x) = f (b).

2) Функция называется непрерывной на отрезке [a,b], если она непрерывна во всех внутренних точках отрезка и непрерывна справа на левом конце и непрерывна слева на правом конце.

88. Свойства функций, непрерывных в отрезке. Точки разрыва и их классификация.

Свойства функций, непрерывных на отрезке:

Теорема (Вейерштрасса): если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений.

Следствие: если функция непрерывна на отрезке, то она ограничена на этом отрезке.

Непрерывность функции в интервале и на отрезке:

Функция y=f(x) называется непрерывной в интервале (a,b),если она непрерывна в каждой точке этого интервала.

Функция y=f(x) называется непрерывной на отрезке [a,b] , если она непрерывна в интервале (a,b) и в точке х=а непрерывна справа (т.е. 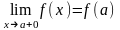), а в точке x=b непрерывна слева ( ).

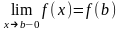Равномерная непрерывность:

Функция f: X → R называется равномерно-непрерывной на множестве X, если

.

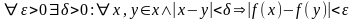классификация точек разрыва.

Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х0, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х0 является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.

Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.

Если односторонний предел , то функция называется непрерывной справа.

Если односторонний предел , то функция называется непрерывной слева.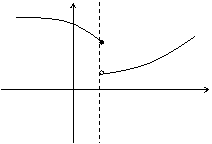

Точка х0 называется точкой разрыва функции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке.

Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.

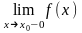
Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х0, достаточно того, что она определена слева и справа от нее.

Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.

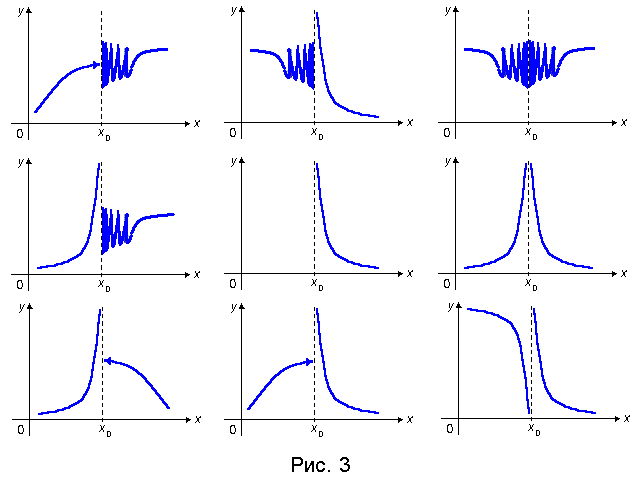
Если значения на концах разрыва совпадают, то для наличия разрыва нужно, чтобы либо эти совпадающие значения были отличны от значения функции в точке , либо функция в этой точке была вовсе не определена. Если в этом случае переопределить (или доопределить) функцию в точке , то полученная изменённая функция будет уже непрерывна в точке и разрыв в точке исчезнет; отсюда и название такого разрыва -- устранимый.