80. Предел суммы, произведения, частного.

1)Предел суммы двух функций равен сумме их пределов: 2)Предел произведения двух функций равен произведению их пределов:

3)Предел частного двух функций равен пределу делимого, деленного на предел делителя, если предел делителя не равен :

81. Теорема о промежуточной функции

одна из простейших теорем, изучаемых в рамках курса математического анализа.

Пусть в некоторой окрестности точки функция заключена между двумя функциями и , имеющими одинаковый предел при , то есть .

Тогда .

Доказательство. Из неравенства получаем неравенство . Условие позволяет предположить, что для любого существует окрестность , в которой верны неравенства и . Из изложенной выше оценки максимумом следует, что при , что удовлетворяет определению предела, то есть .

82. Первый замечательны предел.

При вычислении пределов выражений, содержащих тригонометрические функции, часто используют предел называемый первым замечательным пределом.

Читается: предел отноешния синуса к его аргументу равен единице, когда аргумент стремится к нулю.

Доказательство:

Возьмем круг радиуса 1, обозначим радианную меру угла МОВ через х. пусть 0<x< . На рисунке , дуга МВ численно равна центральному углу х, . Очевидно, имеем . На основании соответствующих формул геометрии получаем . Разделим неравенство на >0, Получим 1<

Так как 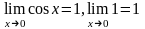, то по признаку ( о пределе промежуточной функции) существования пределов .

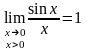А если x<0 => , где –x>0 =>

83. Второй замечательный предел.

Как известно, предел числовой последовательности , имеет предел равный e. . 1.Пусть . Каждое значение x заключено между двумя положительными целыми числами: , где n=[x] – это целая часть x. Отсюда следует 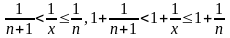, поэтому . Если , то . Поэтому: ,

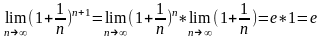. По признаку существования пределов: . 2. Пусть . Сделаем подстановку –x=t, тогда = . и 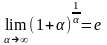называются вторым замечательным пределом. Они широко используются при вычислении пределов. В приложениях анализа большую роль играет показательная функция с основанием e. Функция называется экспоненциональной, употребляется также обозначение .

84. Сравнение б.М функций. Эквивалентные б.М функции.

Две б.м.ф. сравниваются между собой с помощью их отношения.Пусть α=α(х) и ß=ß(х) есть б.м.ф. при х→х_о, т. е.  и 

1. Если  =А¹ 0 (АєR), то α и ß называются бесконечно

малыми одного порядка.

2. Если,  =0, то α називатся бесконечно малой более высокого порядка , чем ß.

3. Если  =∞, то α называется бесконечно малой более низкого порядка, чем ß.

4. Если   не существует, то α и ß называются несравнимыми бесконечно малыми.