Матрицы. Основные понятия. Линейные операции над матрицами и их свойства.
Матрицей размера m на n называется совокупность mn вещественных (комплексных) чисел или элементов другой структуры (многочлены, функции и т.д.), записанных в виде прямоугольной таблицы, которая состоит из m строк и n столбцов и взятая в круглые или прямоугольные или в двойные прямые скобки. При этом сами числа называются элементами матрицы и каждому элементу ставится в соответствие два числа - номер строки и номер столбца.
Матрица, все элементы которой равны нулю, называется нулевой матрицей
Матрица размера n на n называется квадратной матрицей n-го порядка, т.е. число строк равно числу столбцов.
Квадратная матрица называется диагональной, если все ее внедиагональные элементы равны нулю.
Диагональная матрица, у которой все диагональные элементы равны 1, называется единичной матрицей Сложение матриц.
Свойства сложения:
А + В = В + А.
(А + В) + С = А + (В + С) .
Если О – нулевая матрица, то А + О = О + А = А
Замечание 1. Справедливость этих свойств следует из определения операции сложения матриц.
Замечание 2. Отметим еще раз, что складывать можно только матрицы одинаковой размерности.
Умножение матрицы на число.
Свойства умножения матрицы на число
(km)A=k(mA).
k(A + B) = kA + kB.
(k + m)A = kA + mA.
Замечание 1. Справедливость свойств следует из определений 3.4 и 3.5.
Замечание 2. Назовем разностью матриц А и В матрицу С, для которой С+В=А, т.е. С=А+(-1)В. Перемножение матриц.
Умножение матрицы на матрицу тоже требует выполнения определенных условий для размерностей сомножителей, а именно: число столбцов первого множителя должно равняться числу строк второго.
Для квадратных матриц одного порядка произведения АВ и ВА существуют и имеют одинаковую размерность, но их соответствующие элементы в общем случае не равны.
Однако в некоторых случаях произведения АВ и ВА совпадают
Обратная матрица.
Квадратная матрица А называется вырожденной, если ∆А=0, и невырожденной, если∆А≠0
Квадратная
матрица В называется обратной к
квадратной матрице А того же порядка,
если АВ = ВА = Е. При этом В обозначается
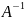
Для существования обратной матрицы необходимо и достаточно, чтобы исходная матрица была невырожденной.
Определитель матрицы. Свойства определителей.
Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца. (∆А)
Свойства определителей
Определитель — кососимметричная полилинейная функция строк (столбцов) матрицы. Полилинейность означает, что определитель линеен по всем строкам (столбцам): , где и т. д. — строчки матрицы, — определитель такой матрицы.
При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится.
Если две строки (столбца) матрицы совпадают, то её определитель равен нулю.
Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю.
Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1).
Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.
Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю.
Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю.
Сумма произведений всех элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
Определитель произведения квадратных матриц одинакового порядка равен произведению их определителей (cм. также формулу Бине-Коши).
С использованием индексной нотации определитель матрицы 3×3 может быть определён с помощью символа Леви-Чивита из соотношения:
