61) Потеря устойчивости прямого стержня под действием осевой сжимающей силы. Критические напряжения

При расчете элементов строительных конструкций на сжатие используется метод расчета на устойчивость при помощи коэффициента уменьшения основного допускаемого напряжения .

Из курса сопротивления материалов известно, что критическая сила, сжимающая прямой стержень, вычисляется с помощью формулы Эйлера

, (6.1)

где – коэффициент приведенной длины, зависящий от условий закрепления стержня.

Зная критическую силу, вычисляют критическое напряжение и условие применимости формулы Эйлера

, (6.2)

где - предел пропорциональности стали.

Подставив выражение для критической силы, получаем

, (6.3)

где – радиус инерции сечения;

– гибкость стержня.

Таким образом, критическое напряжение зависит только от модуля упругости и гибкости стержня .

Если , а для хрупких материалов , то этим напряжениям соответствует гибкость _.

Стержни, у которых гибкость называются стержнями малой гибкости. В этом случае сжатые элементы рассчитывают только на прочность.

В случае стержней большой гибкости опасным состоянием следует считать момент возникновения в сжатом стержне напряжения .

Условие работоспособности сжатого стержня

На практике критическое напряжение вычисляют в зависимости от расчетного сопротивления

, (6.4)

где – коэффициент продольного изгиба (коэффициент уменьшения допускаемого напряжения на сжатие). Его определяют в зависимости от гибкости , расчетного сопротивления и модуля упругости (модуля Юнга) .

62)Расчет центрально сжатых колонн

6.1. Расчет центрально сжатых колонн

Центрально сжатыми называются колонны, нагруженные сжимающими силами, направленными вдоль оси колонны (рис. 41). Такие колонны необходимо рассчитывать на прочность и устойчивость.

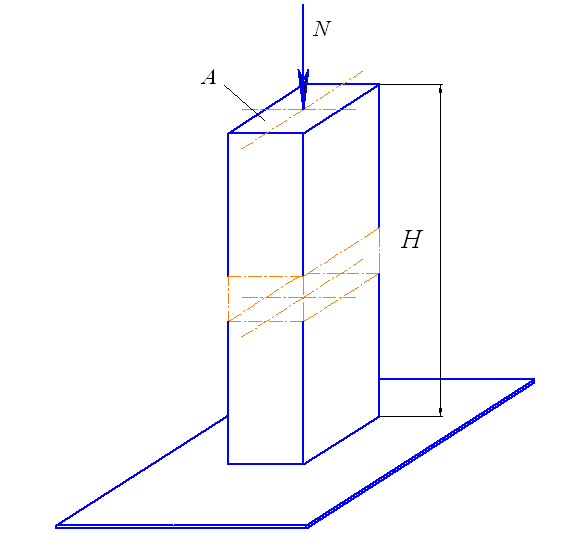
Рис 41. Центрально сжатая колонна

Условие прочности отражает первое предельное состояние

, (6.5)

где – сжимающая сила;

– площадь сечения колонны.

Условие устойчивости формулируется с использованием коэффициента продольного изгиба (уменьшения допускаемого напряжения на сжатие)

. (6.6)

Коэффициент определяется в зависимости от гибкости колонны

, (6.7)

где – расчетная длина колонны, которая принимается равной высоте колонны;

– радиус инерции поперечного сечения.

При вычислении гибкости колонны коэффициент приведенной длины принимается как для случая шарнирного закрепления по концам колонны, т.е. . Такое условие можно принять для случая свободного опирания траверсы, несущей трубопроводы, на колонну сверху и полагая, что соединение базы колонны с фундаментом не создает защемления нижнего конца колонны в силу того, что существует возможность изгиба опорной плиты.

Коэффициент вычисляют в зависимости от величины условной гибкости колонны

. (6.8)

Значения  следует определять по формулам СНиП II-23-81

(6.9)

(6.10)

. (6.11)

При этом гибкость колонны не должна превышать предельной гибкости

(6.12)

где

a – коэффициент, принимаемый не менее 0,5.

Исходя из условия предельной гибкости, можно рекомендовать предельные размеры при проектировании колонн.

Так, например, для сварных двутавровых колонн принимается:

• толщина листов для поясов двутавра ;

• толщина листов для стенки двутавра .

Высоту двутаврового сечения (рис. 42) принимают в зависимости от высоты колонны

. (6.13)

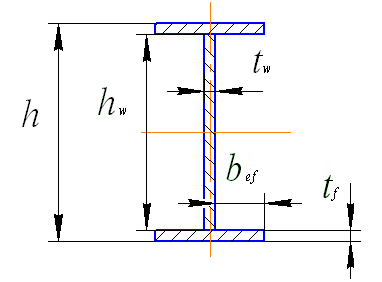
Рис 42. Обозначение размеров поперечного сечения двутавра

Для соотношения геометрических размеров поперечного сечения в зависимости от гибкости

(6.14)

(6.15)

(6.16)

Для укрепления контура сечения и стенки колонны, при отношении , устанавливают парные поперечные ребра жесткости на расстоянии 2,5-3 м, но не менее 2-х на одном отправочном элементе.

Если в результате расчета требуется вычислить площадь поперечного сечения но в этом случае коэффициент продольного изгиба не известен, поскольку он сам зависит от площади поперечного сечения.

Для разрешения этого противоречия используется метод последовательных приближений для подбора коэффициента . Первоначально можно принять . После этого вычисляют площадь сечения и уже для этой величины площади подбирают размеры сечения. Установив размеры поперечного сечения колонны и определив геометрические характеристики , и , устанавливают фактическое значение .

При второй попытке и т.д. пока не выполнится условие , где наперед заданная малая величина.

63)Расчет внецентренно сжатых колонн.