Железобетонные конструкции

Железобетон состоит из бетона и располомженных в нем стальных стержней, которые называются арматурой. Стальная арматура составляет с бетоном монолит, который в процессе нагружения деформируется совместно.

Бетон обладает значительным сопротивлением сжимающим напряжениям и весьма малым сопротивлением растяжению. Прочность бетона на растяжение в 10-15 раз меньше прочности на сжатие.

Сталь отлично работает на растяжение. Поэтому в железобетоне сжимающие напряжения воспринимаются бетоном, а растягивающие – стальной арматурой.

В изгибаемых железобетонных элементах рабочую арматуру размещают обычно в растянутой зоне в соответствии с эпюрой изгибающего момента.

Кроме экономических железобетон обладает рядом других важных технических преимуществ:

повышенная долговечность благодаря надежной сохранности арматуры, заключенной в бетон;
прочность со временем не уменьшается;
хорошее сопротивление атмосферному воздействию;
высокая огнестойкость;
возможность изготовления деталей и несущих элементов любой конструктивной и архитектурной формы;
малые затраты времени на изготовление и монтаж строительных конструкций.

Бетон

Бетон, как искусственный строительный материал, получается в результате затвердевания уплотненной смеси вяжущего вещества, воды, заполнителей и добавок.
Бетон должен обладать высокой прочностью, хорошим сцеплением с арматурой и плотностью, которая обеспечивает сохранность арматуры от коррозии и долговечность конструкции.
Физико-химические свойства бетона зависят от состояния смеси, вида вяжущего вещества, добавок и заполнителей, способов приготовления бетона, условий затвердевания, возраста бетона и др.
Наиболее широкое применение в строительстве получили обычные тяжелые бетоны плотностью 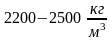, приготовляемые на основе обычных плотных заполнителей.
Материалы относят к плотным (нерудные строительные материалы, щебень и песок из отходов промышленности), если плотность зерен составляет свыше 2,0 г/см³ и к пористым (пористые заполнители) - если плотность зерен - до 2,0 г/см³.
В зависимости от объемной массы бетоны подразделяются на особо тяжелые 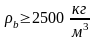, тяжелы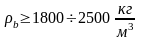е , легкие 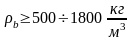и особо легкие 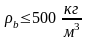. По виду вяжущего вещества цементные, силикатные, гипсовые, асфальтобетоновые, полимербетоновые и другие. По назначению различают обычные бетоны, гидротехнические, дорожные, теплоизоляционные, декоративные, специального назначения (химическистойкие, жаростойкие, от ядерного излучения).
Основным показателем качества бетона является прочность при сжатии, по которому устанавливается его марка.

Диаграмма испытаний бетонных образцов

При однократном нагружении бетонных образцов сжимающими нагрузками диаграмма напряжения – деформации ( ) имеет криволинейный характер (рис. 14). В бетоне одновременно с упругими деформациями развиваются и неупругие деформации, обусловленные ползучестью, т.е. способностью образца деформироваться во времени при неизменной нагрузке.

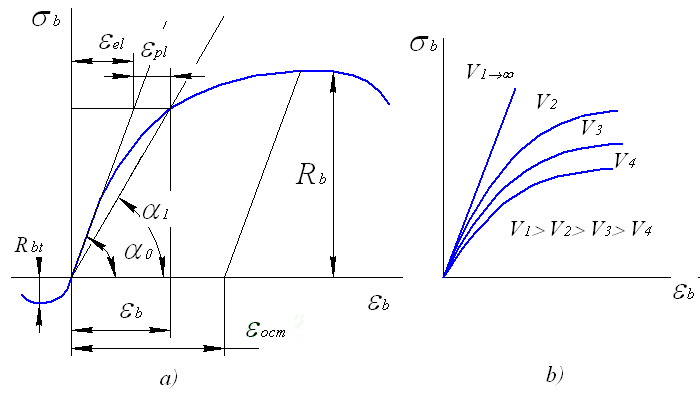
Рис.14. Диаграмма испытаний бетонных образцов
При очень быстром (мгновенном) нагружении бетонного образца деформации, возникающие в нем, пропорциональны прикладываемым нагрузкам, т.е. выполняется закон Гука. Отражением такого характера деформирования бетонного образца является прямая, проведенная из начала координат по касательной к действительной диаграмме , а тангенс угла наклона этой касательной к оси абсцисс называется модулем упругости бетона
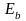
(3.3)
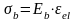, (3.4)
где 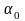– угол, характеризующий упругие деформации в бетоне;
– напряжения в бетонном образце;
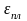– упругая составляющая деформаций образца.
Если образец нагружать ступенчато, то диаграмма примет также ступенчатый вид. Наклонные линии будут отражать упругие деформации, а горизонтальные площадки – неупругие деформации, вызванные ползучестью бетона.
Тогда в любой момент нагружения общие деформации будут определяться суммой упругих и пластических деформаций
, (3.5)
где 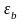– общая деформация бетонного образца;
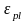– пластическая составляющая общих деформаций.
С уменьшением скорости нагружения бетонного образца кривые деформаций все больше отклоняются от прямой линии упругих деформаций, как это видно на диаграмме (рис. 14, b).
Особо следует подчеркнуть, что в процессе разгрузки ещё не разрушившегося образца зависимость будет иметь практически прямолинейный характер. На диаграмме это будет отражаться прямой параллельной линии упругих деформаций (α₀), при этом в образце возникнут остаточные деформации .
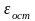Развитие полных деформаций будет характеризоваться модулем упругопластичности или модулем деформации бетона
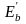
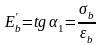, (3.6)
где 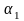– угол наклона секущей кривой полных деформаций (рис. 14).
С целью разделения свойств бетона вводятся коэффициенты упругости и пластичности бетона.
Коэффициент упругости бетона
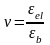. (3.7)
Практические значения коэффициента упругости изменяются в следующих пределах 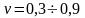. Предельным граничным значениям соответствуют идеальная упругость и идеальная пластичность .
Коэффициент пластичности бетона
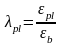. (3.8)
С увеличением и продолжительности действия нагрузки на бетонный образец коэффициент упругости уменьшается.
Очевидна связь между коэффициентами упругости и пластичности бетона
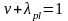, (3.9)
Модуль упругопластичности бетона выражается через коэффициенты упругости и пластичности
. (3.10)
При растяжении диаграмма деформирования бетона также как и при сжатии криволинейная.
Модули упругости бетона принимаются одинаковыми при сжатии и растяжении.
Соответственно модуль упругопластичности бетона 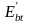при растяжении будет выражаться через коэффициенты упругости и пластичности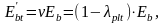
(3.11)
где – индекс обозначающий испытание бетонного образца при растяжении;
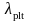– коэффициент пластичности бетона при растяжении.
Величина модуля упругости с увеличением прочности бетона возрастает. Для обычного бетона средняя величина ≈ 27000 – 39000 МПа, т.е. в 5-8 раз меньше модуля упругости стали.
Коэффициент Пуассона с увеличением напряжений возрастает, его первоначальное значение .
Модуль сдвига бетона 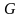зависит от его модуля упругости и коэффициента Пуассона