20.Распределение Больцмана.

Пусть мы находимся на уровне моря(нулевой уровень). -давление на этой поверхности.

П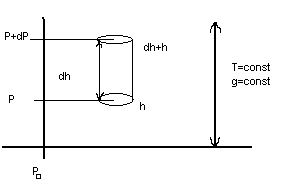 ри : . Предположим, что площадь основания цилиндра ровна 1. для .

, т.к. . Если , то , ,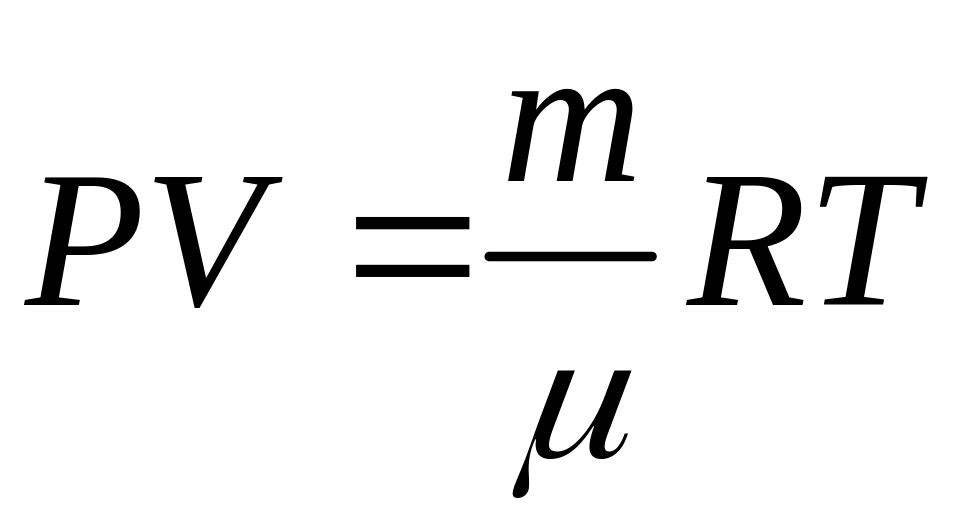 , ,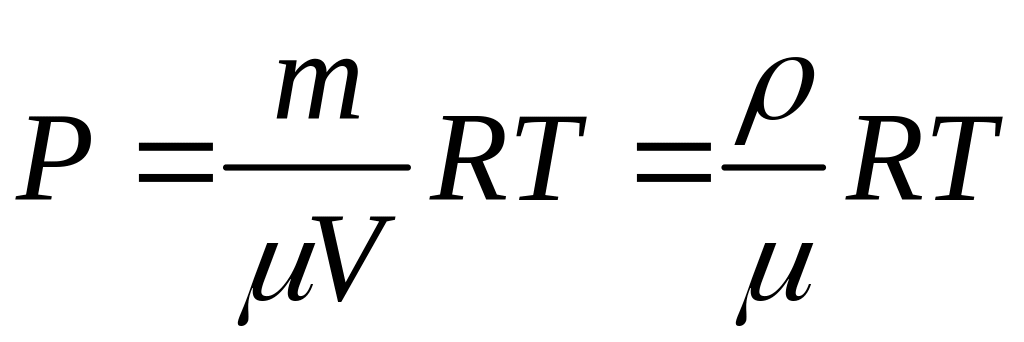 , ,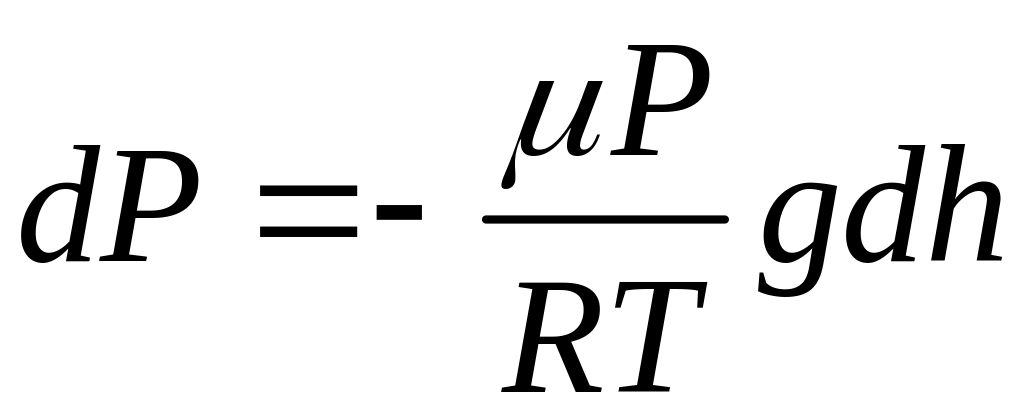 , 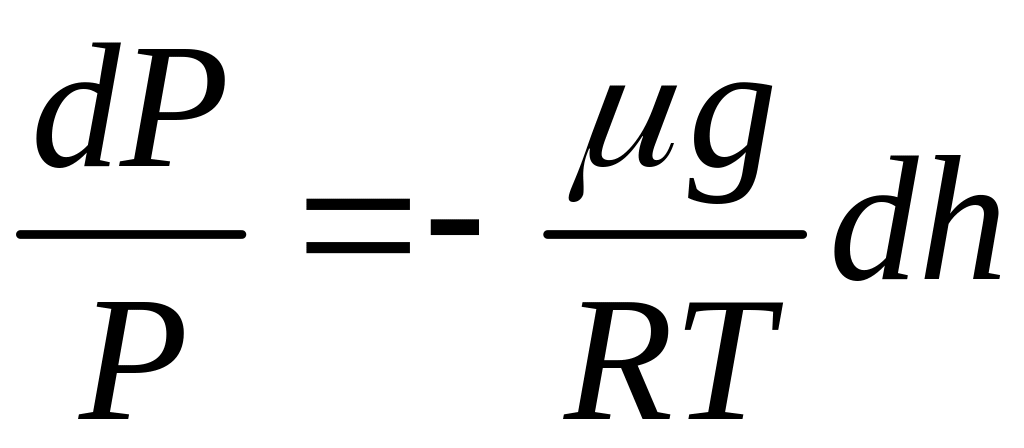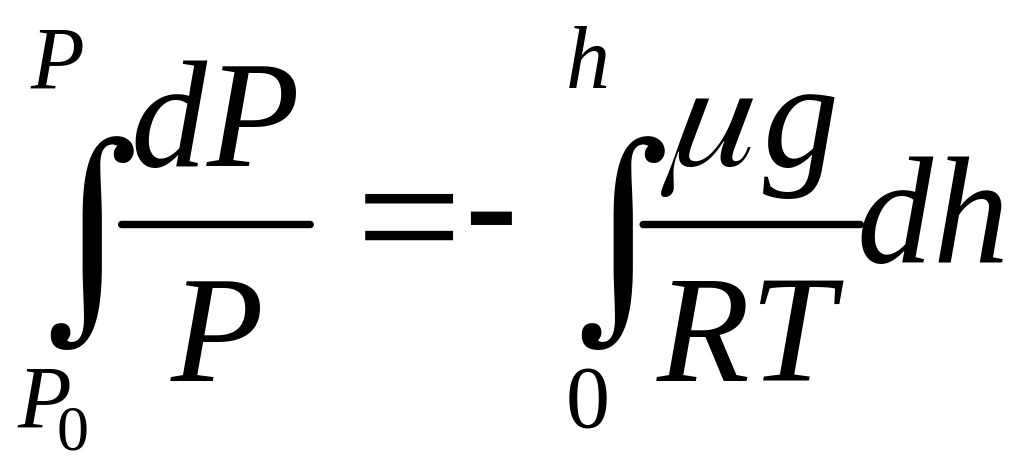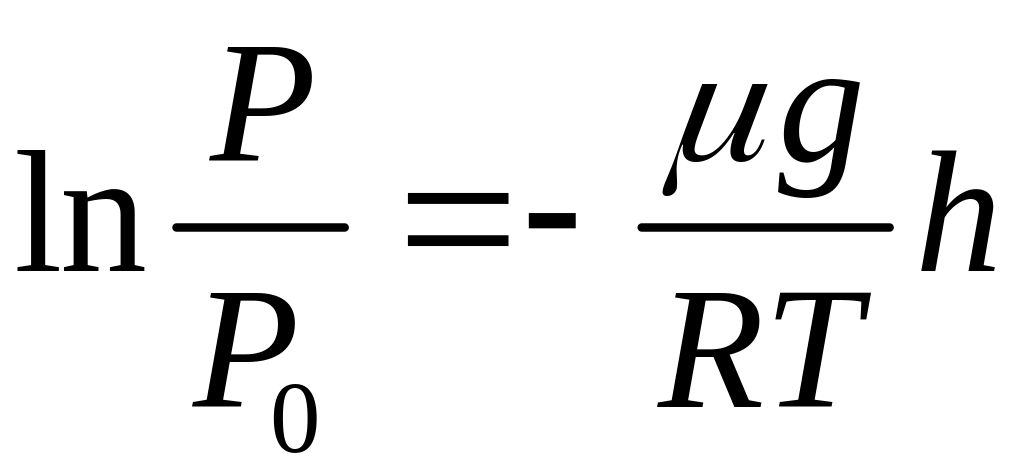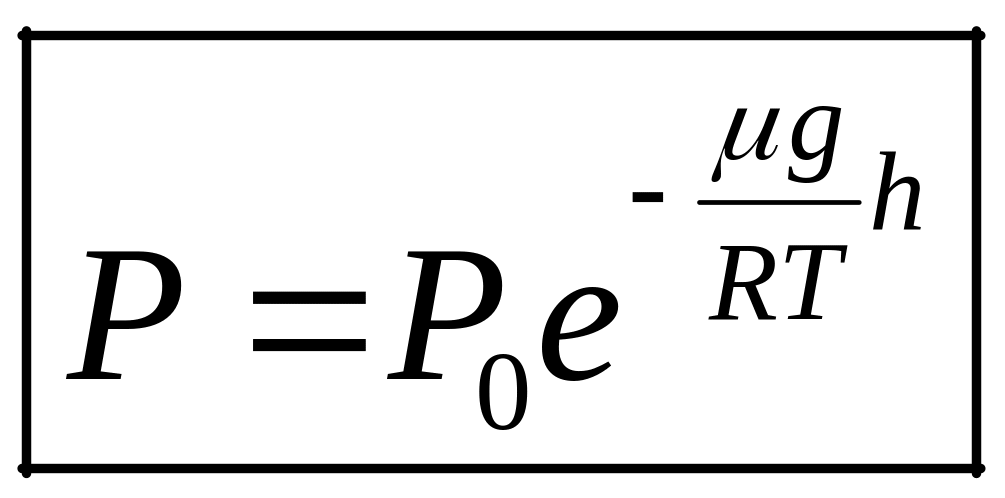-параметрическая формула, , , 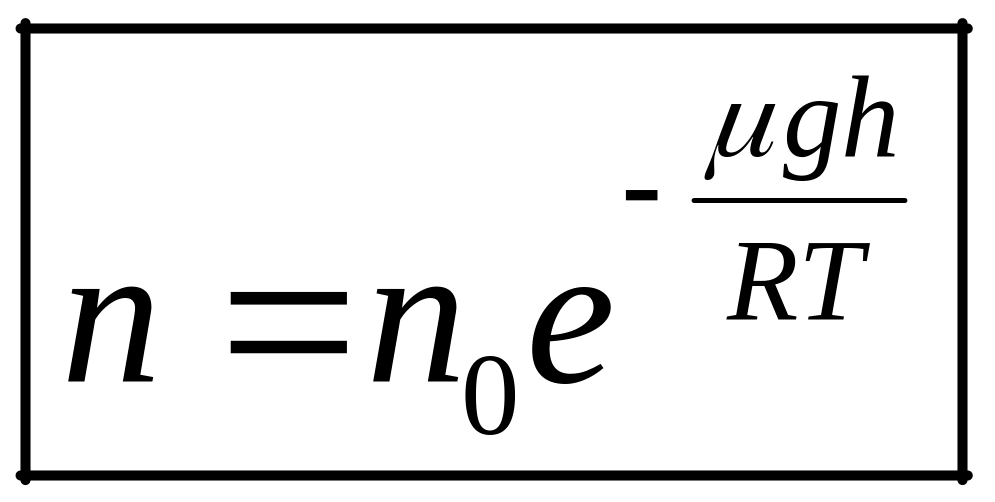-распределение Больцмана.

П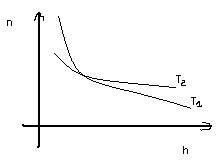 ри , (Т-повышается) .

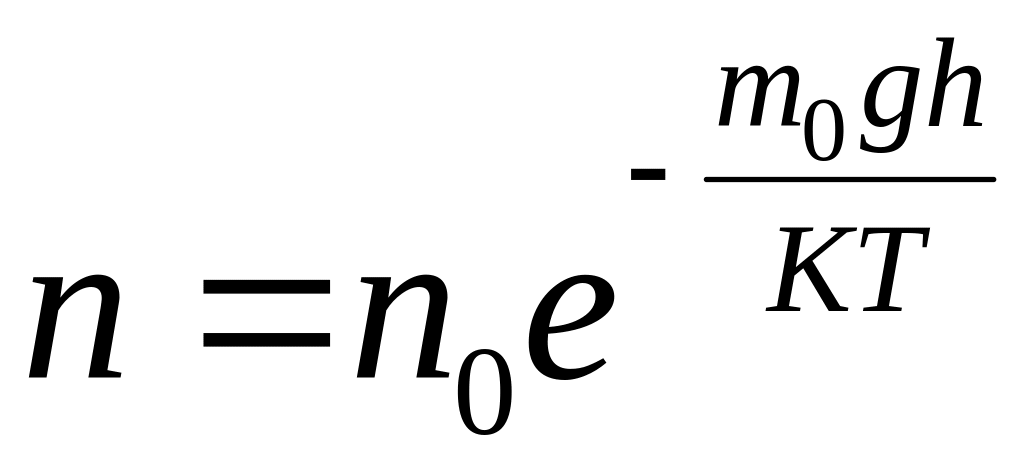, (*). Величина -потенциальная энергия, кот. обладает молекула на данной высоте. Тогда 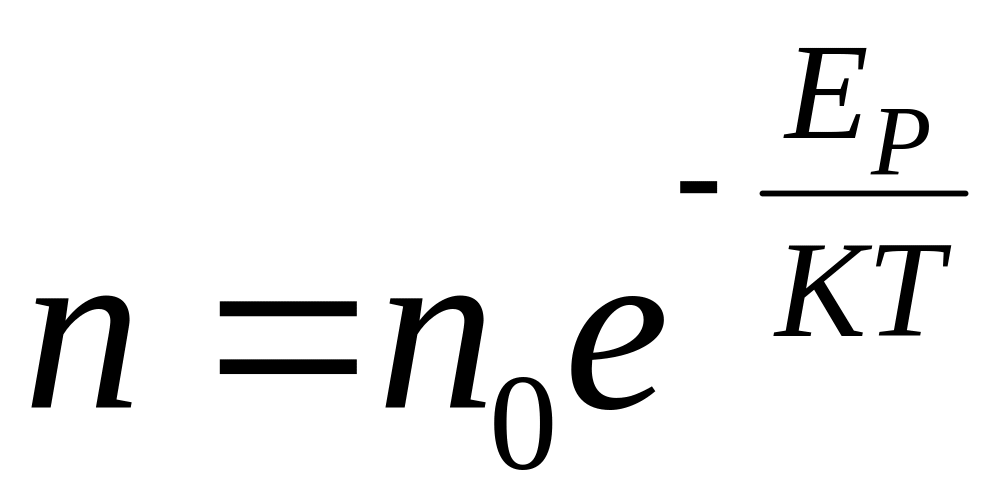, -доля молекул для высоты с энергией .

Существ. в атмосфере распределения молекул воздуха по высоте устанавливается в результате действия двух факторов: 1) под действием силы тяжести молекула стремится опустится на поверхность Земли. 2) Тепловое движение, характеризуемое величиной , стремится распределить молекулы равномерно по высотам.

Формула (*) определяет распределение молекул по высоте и выражает также распределение их по значениям потенц. энергии справедливо не только для поля силы тяжести, но и для любого поля потенц. сил.

21. Опытное обоснование мкт (опыт Штейна, броуновское движение, опытное определение постоянной Авогадро).

1. Суть опыта Штейна: берём платиновую проволоку, покрываем её серебром и располагаем по оси цилиндра. Внутри цилиндра находится ещё один цилиндр с прорезью, через которую был удалён воздух. Проволока разогревалась, атомы серебра испарялись и летели в разные стороны.

2. Опытное определение постоянной Авогадро:

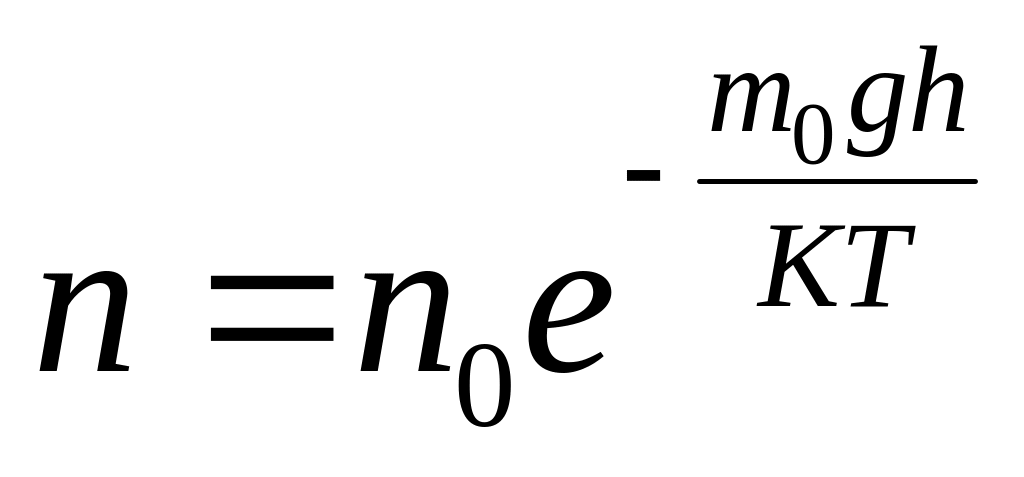- концентрация на различных уровнях

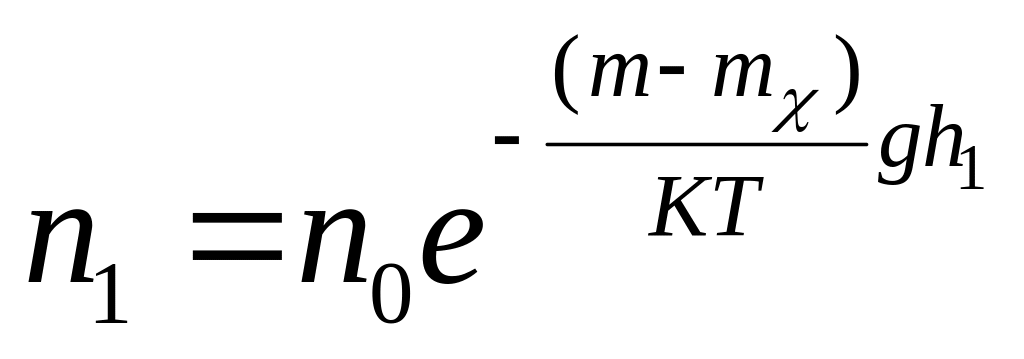
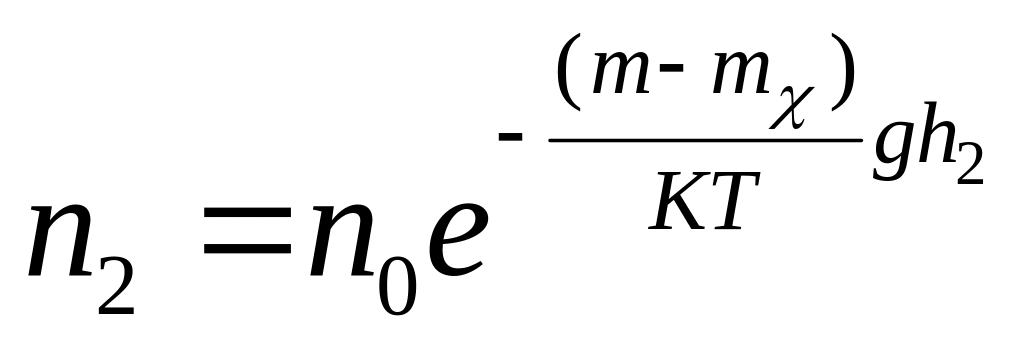
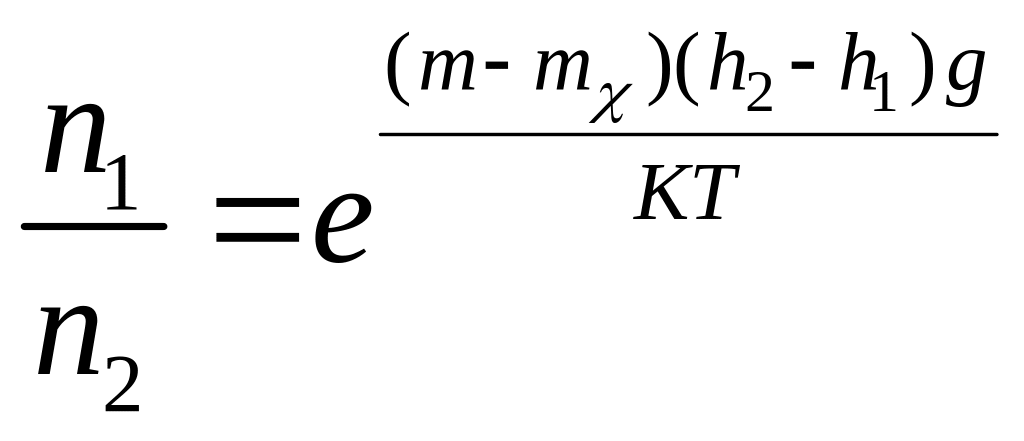
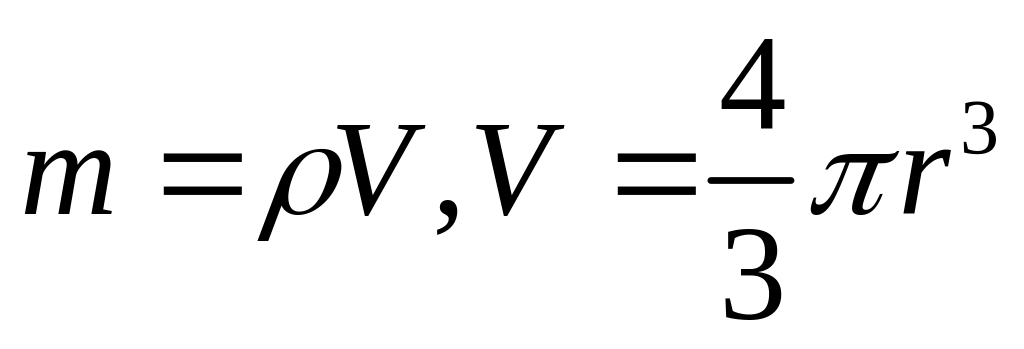
Тогда масса частицы равна

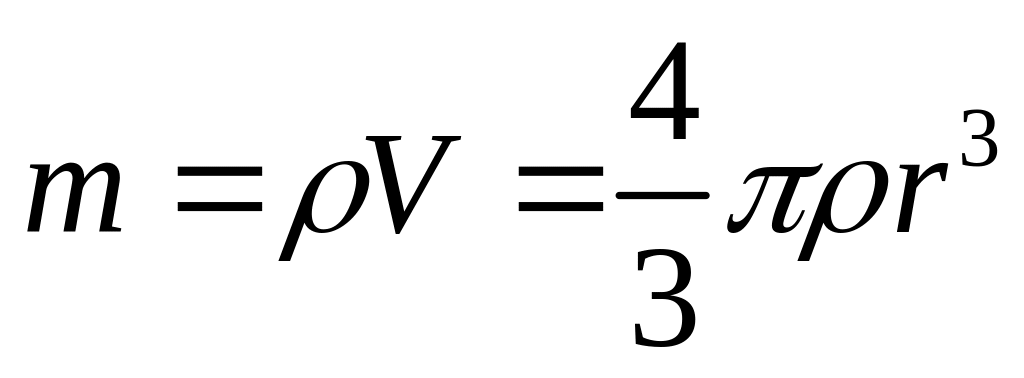
Тогда масса жидкости равна

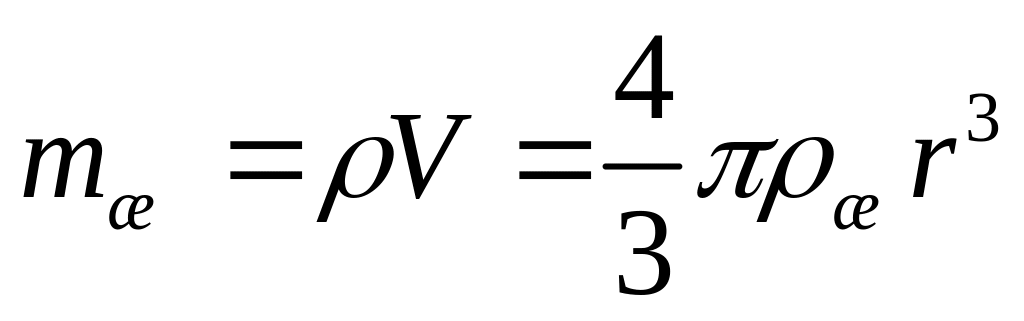
Следовательно,

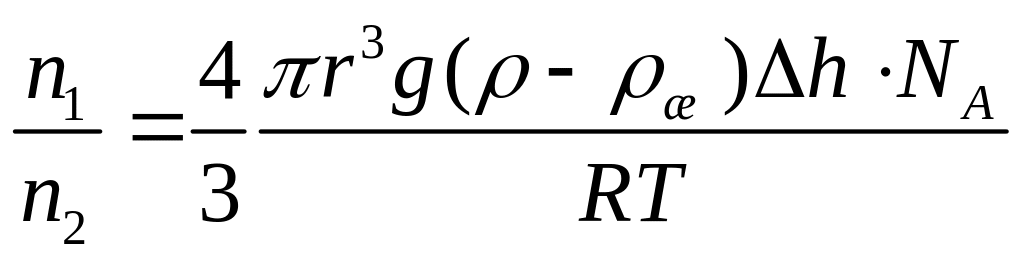
Число Авогадро

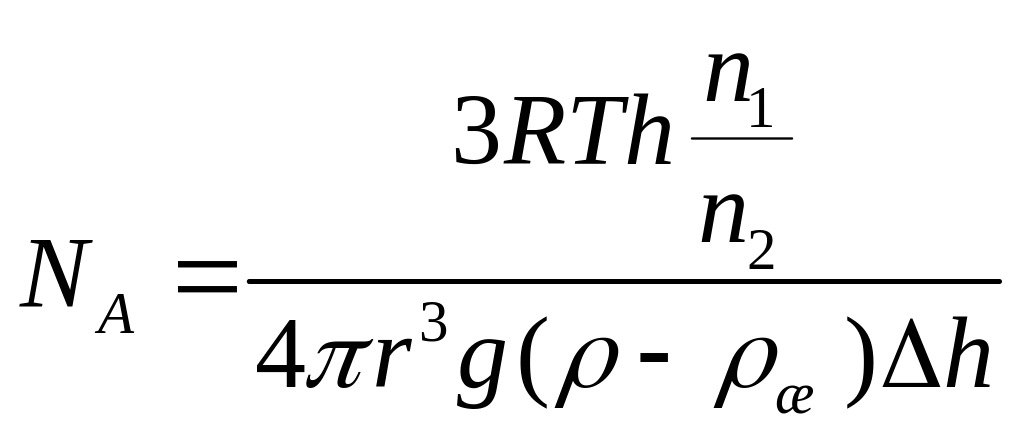
22. Внутренняя энергия. Закон Больцмана о равномерном распределении энергии по степеням свободы молекул.

Под внутренней энергией термодинамической системы понимаем все виды энергии, кроме механической энергии системы (кинетической и потенциальной).

Внутренняя энергия – функция состояния системы и является полным дифференциалом. Свяжем молекулы (одноатомные, двухатомные и трёхатомные с xyz).

1.Одноатомная молекула

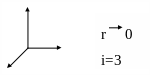
2. Двухатомная молекула

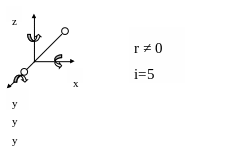
3. Трёхатомная молекула

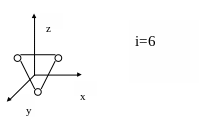
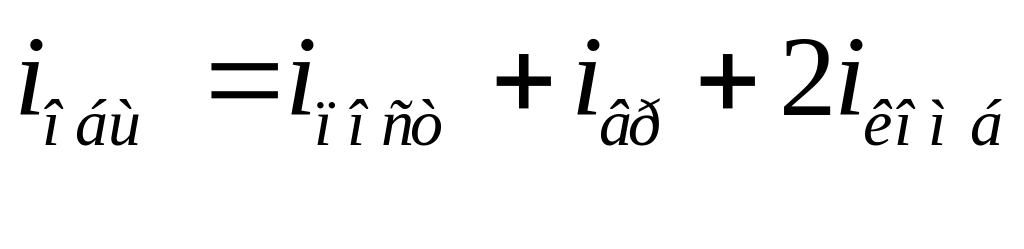
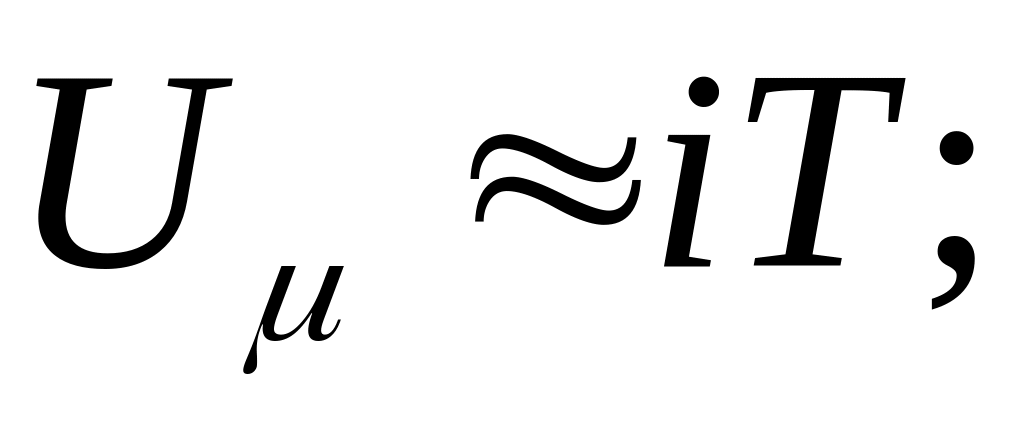
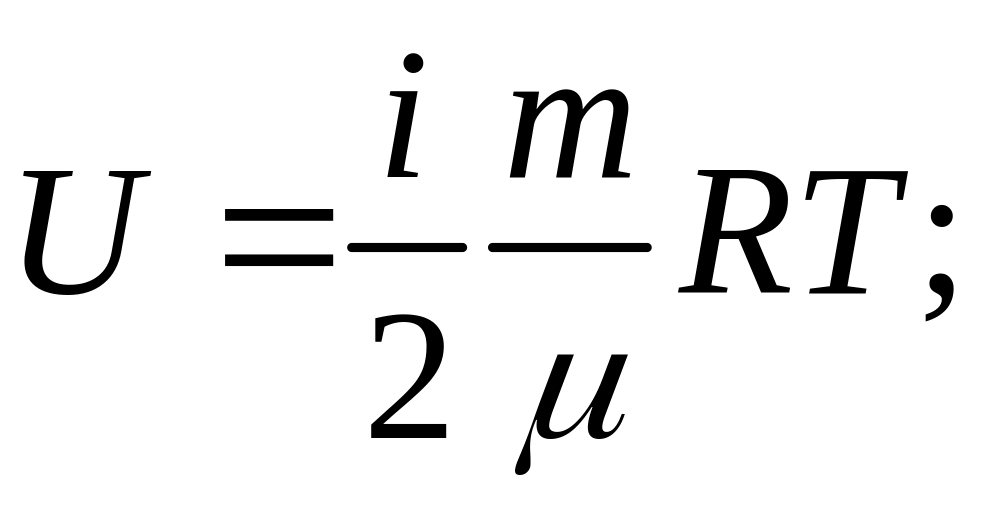
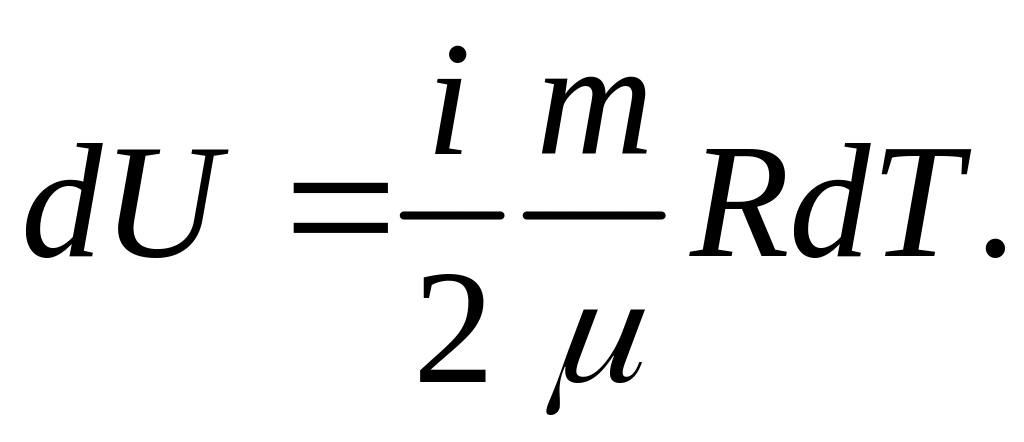
23. Работа и теплота. Пнт.

- элементарная работа

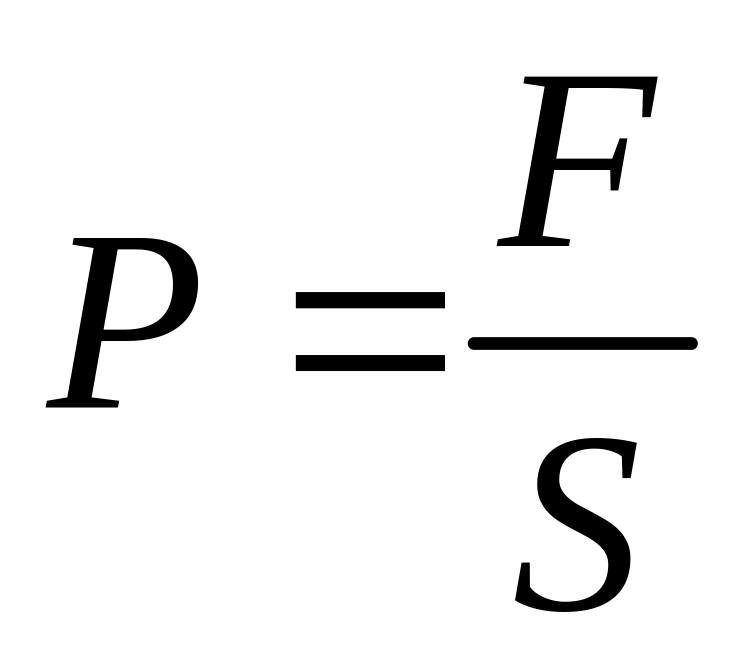- давление

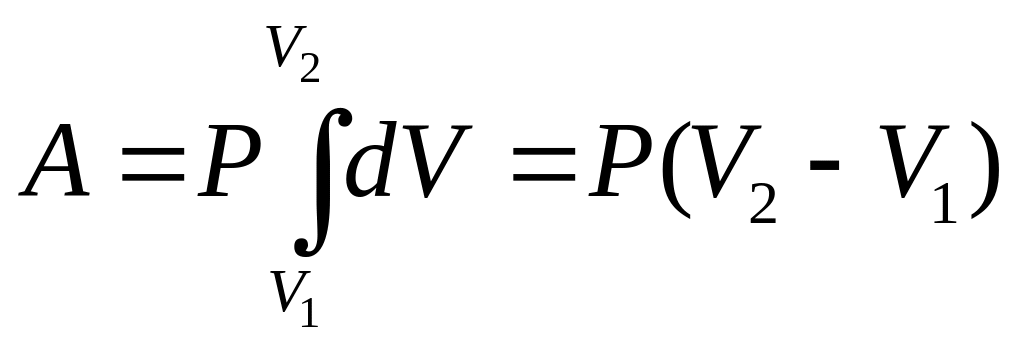(если Р - постоянное)

1. при ΔV>0, ΔA>0 – работа выполняется против внешних сил

2. при ΔV<0, ΔA<0

3. при ΔV=0, ΔA=0

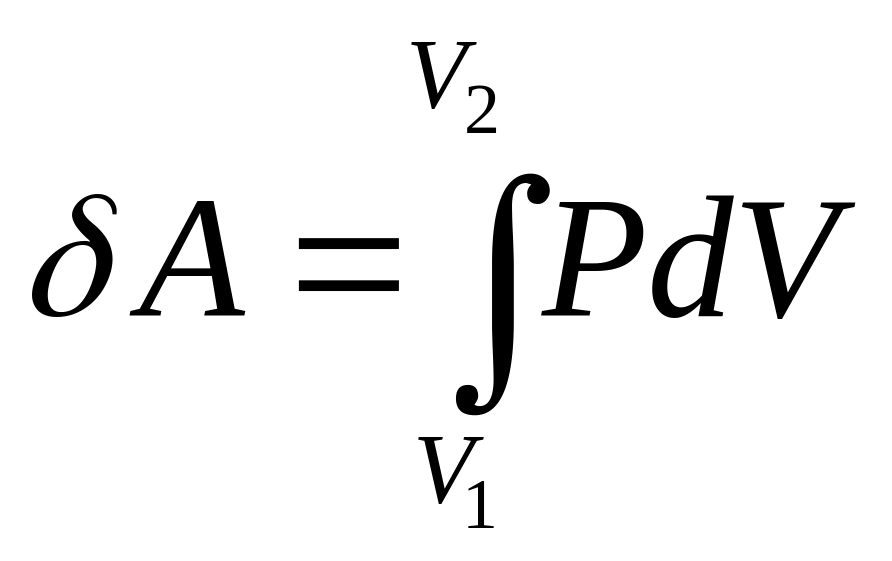
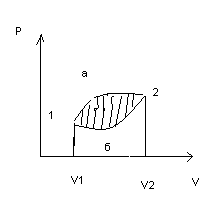
Количество теплоты есть мера изменения той части внутренней энергии, которая обусловлена хаотическим движением частиц, образующих систему. Количество теплоты, получаемая или отдаваемая системой, зависит от пути перехода, поэтому элем. изменение теплоты не является дифференциалом ф-ии параметра системы, т. е. функционал δQ, процесс совершения системой работы и процесс передачи тепла – это качественные различные формы передачи энергии. Работа проявляется в передаче энергии упорядоченного движения, а теплота – в передаче движения хаотического движения частиц.

1. ΔQ=ΔU+A

2. δQ=dU+δA

Эти два выражения – матем. Выражения ПНТ(1. в интегральной форме, 2. в дифференциальной форме)

В диф. форме ПНТ: количество теплоты δQ, сообщённая системой, равно сумме изменения её внутр. энергии dU и работы, совершаемой системой над внешней средой.

В интегр. форме ПНТ: полное количество теплоты Q, полученное системой, идёт на превращение её внутренней энергии и на совершение работы над внешней средой.