7. Механическая система. Импульс механической системы. Закон сохранения импульса.
Совокупность материальных точек и тел, рассматриваемых как единое целое наз. механической системой.
Силы взаимодействия между материальными точками механической системы наз. внутренними.
Силы, с которыми на матер. точки системы действуют внешние тела, наз. внешними.
Механ. система тел, на котор. не действуют внешние силы или результирующая внешних сил равна 0, наз. замкнутой (изолированной).
- массы точек,
- их скорости,
- результат внутр. силы,
- результат внешн. силы.
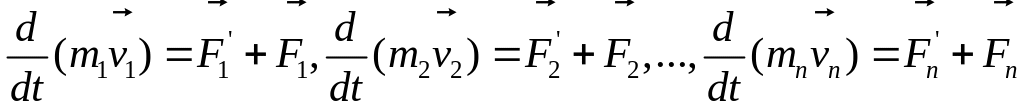
Сложив левые и правые части данных равенств, получим:
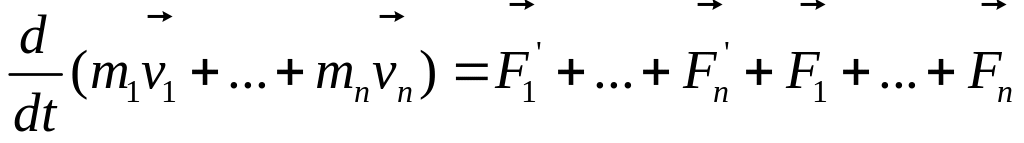
В силу 3-го закона
Ньютона -
,
тогда
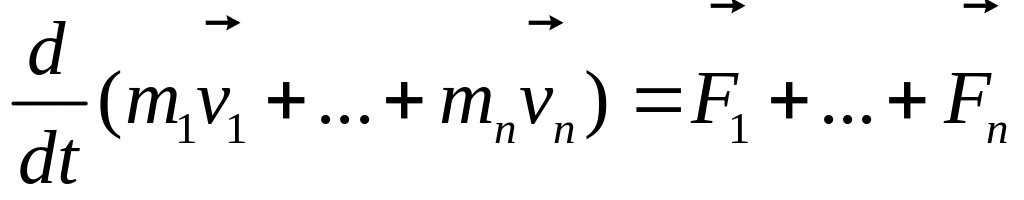
Обозначим
,
тогда
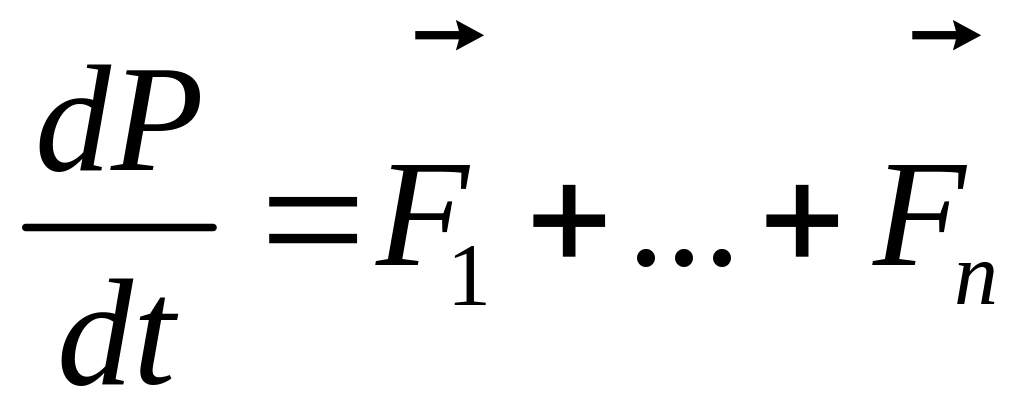- закон движения для механ. системы.
Производная от импульса механ. системы по времени равна векторной сумме внешних сил, действующих на механ. систему.
Пусть механ система
замкнута, т. е. на нее не действуют никакие
силы и результирующая этих сил равна
0, т. е.
.
Тогда
.
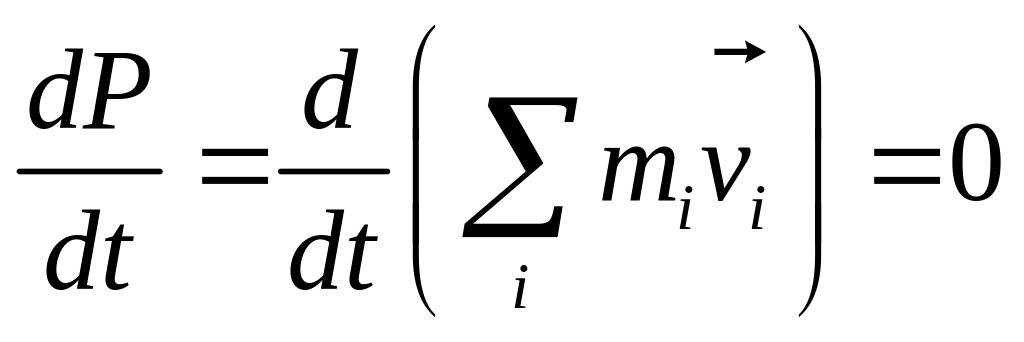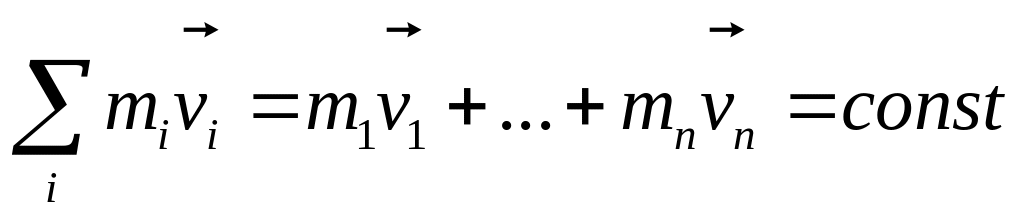
Импульс механической системы есть величина постоянная, при условии, что система замкнута (закон сохранения импульса).
Центр масс. Центр тяжести механической системы. Закон движения центра масс.
Центром масс
наз.
воображаемая точка
положение
котор. характеризует распределение
масс этой системы.
,
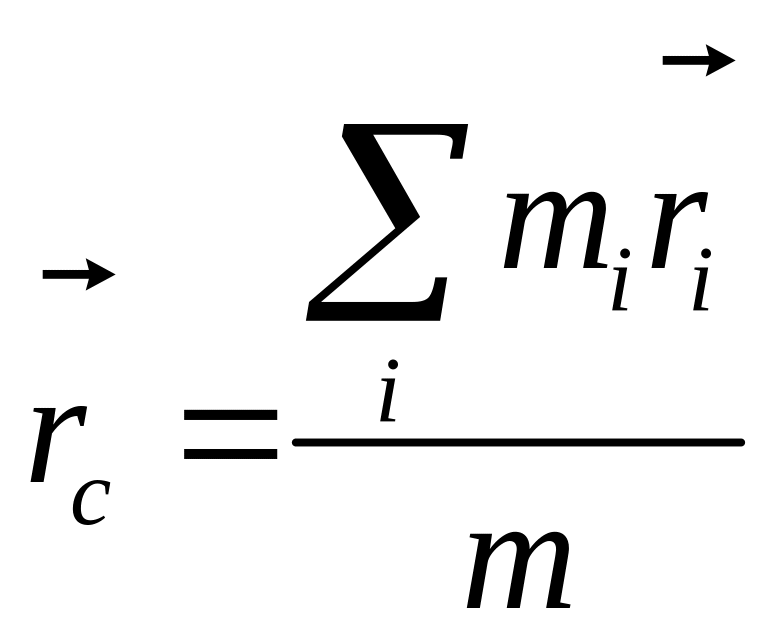где
,
,
;
,
;
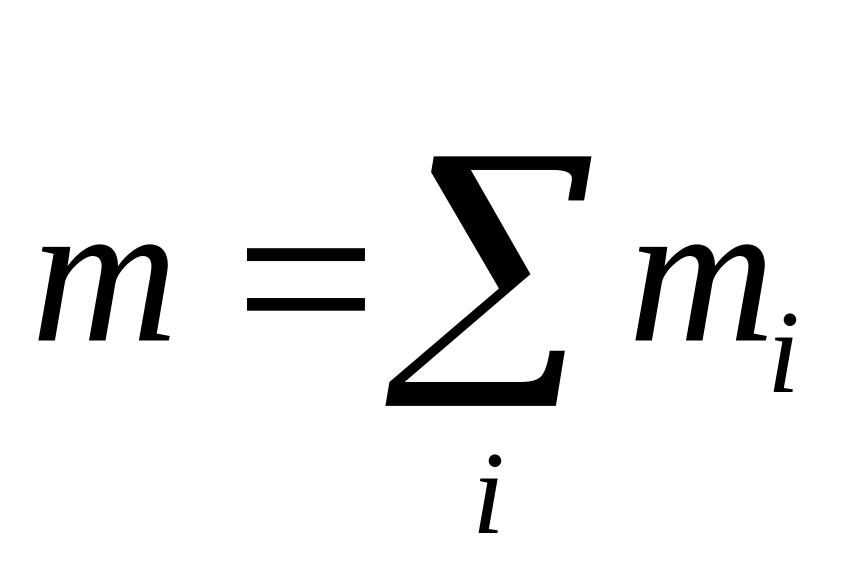
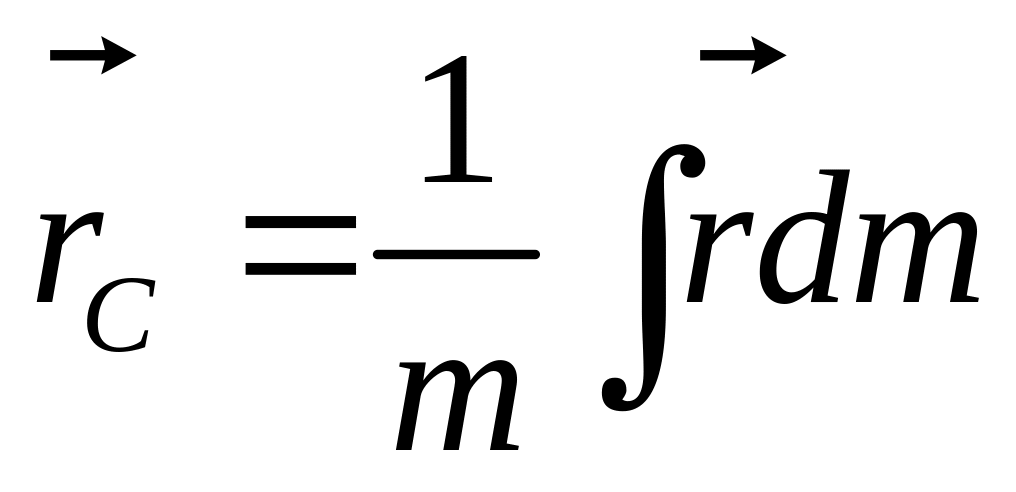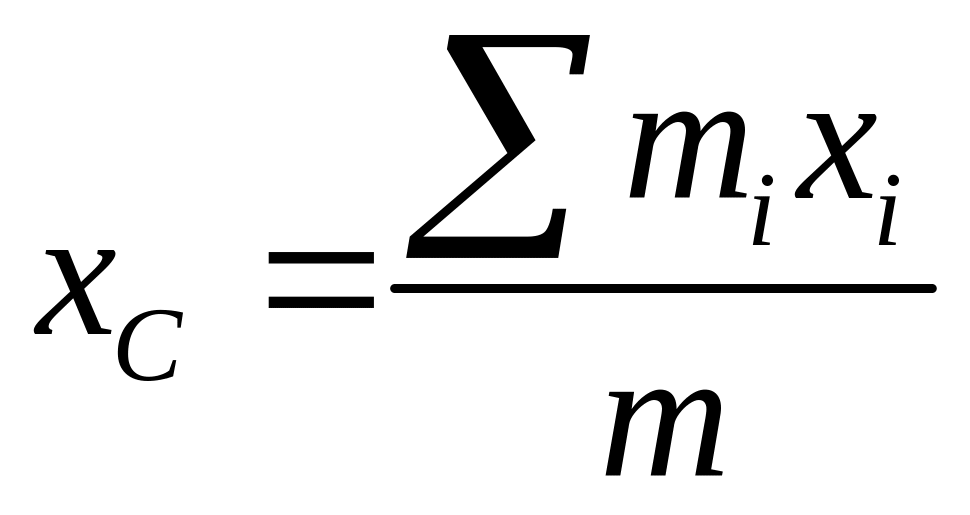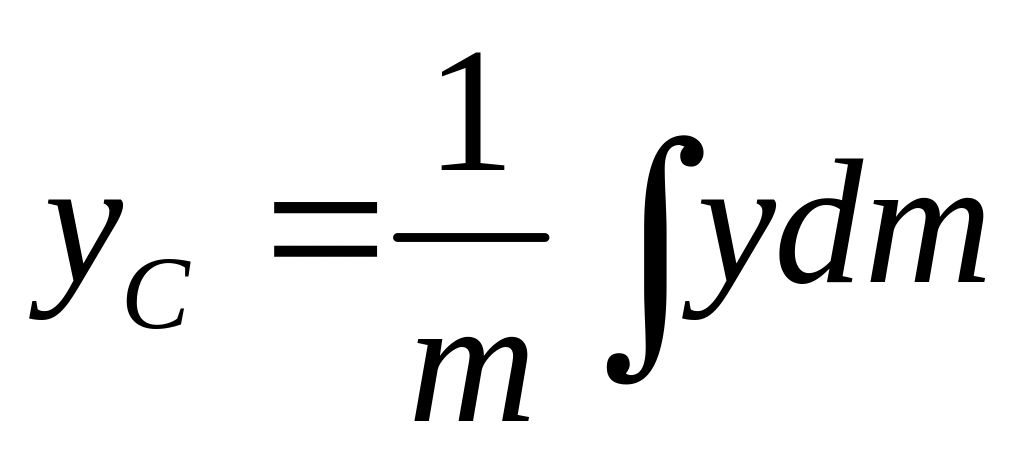
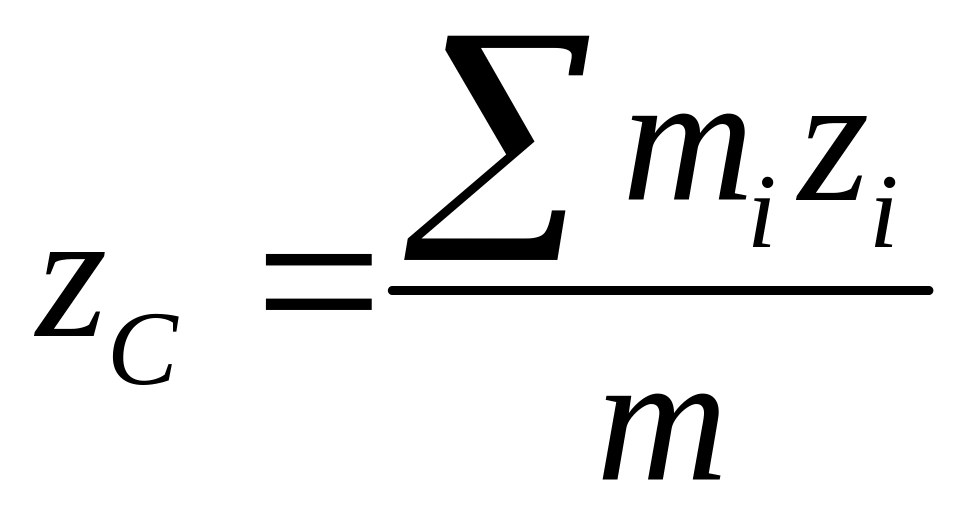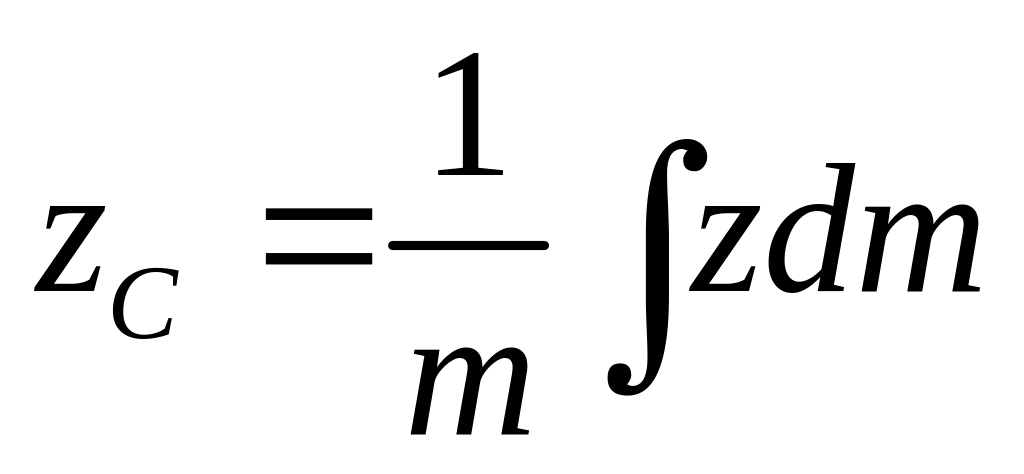
Скорость центра масс (вектор скорости)
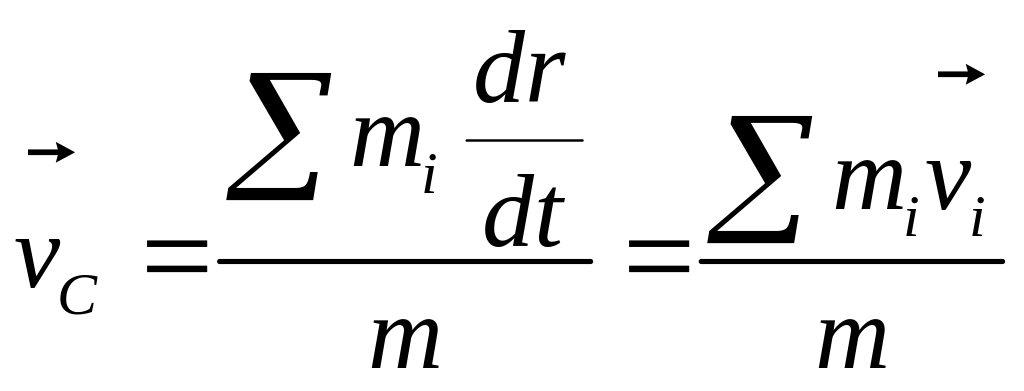
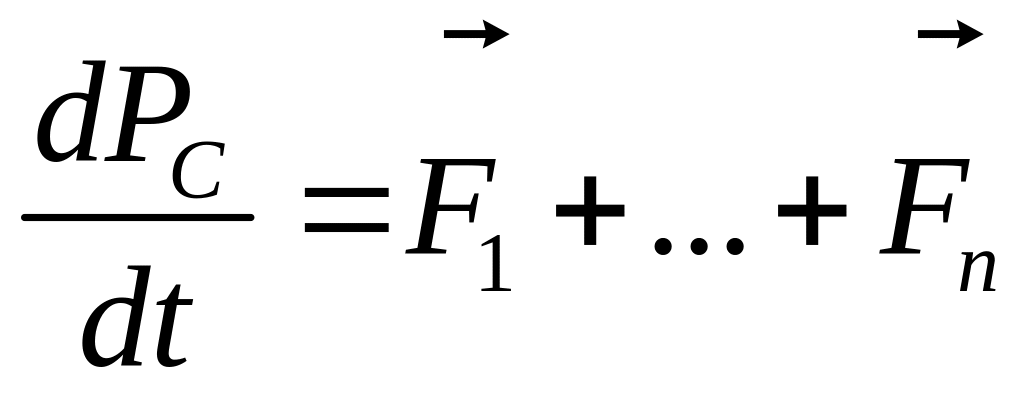- закон движения
центра масс.
Центр масс системы движется как матер. точка, в котор. сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме внешних сил, действ. на систему.
Очевидно, что
.
Из закона сохранения импульса
что центр масс либо покоится, либо
движется равномерно и прямолинейно.
8. Энергия, работа, мощность. Кинетическая и потенциальная энергия.
Энергия – универсальная количественная мера движения и взаимодействия всех видов материй.
.
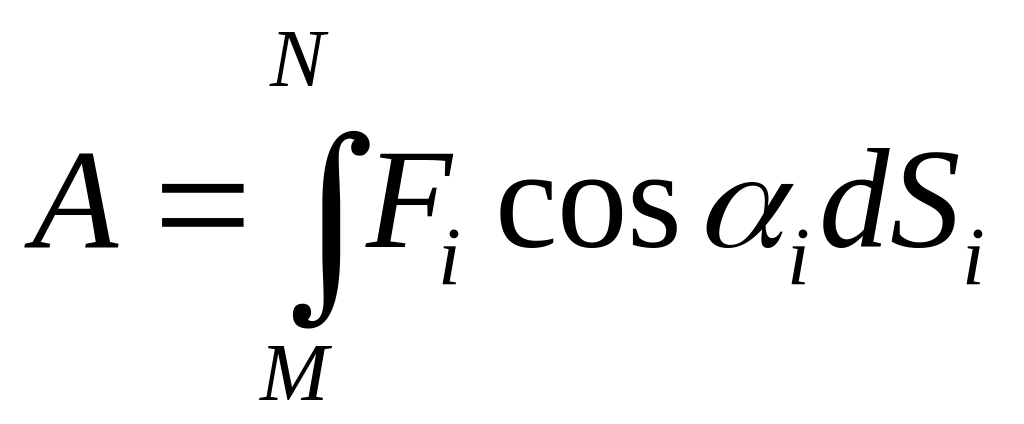- работа.
Пусть сила задается графически:
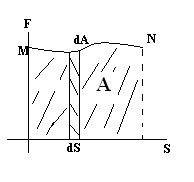
Если
,
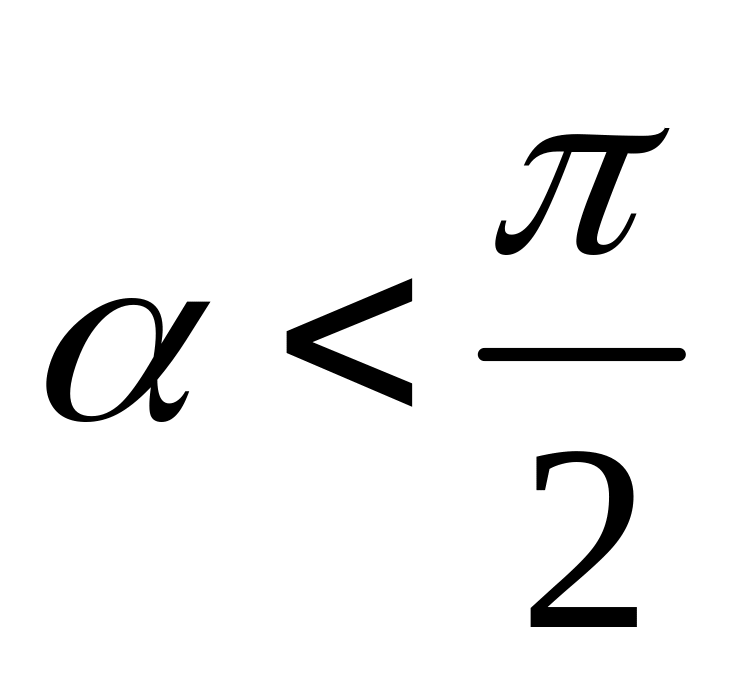то А>0 (движущая сила).
Если
,
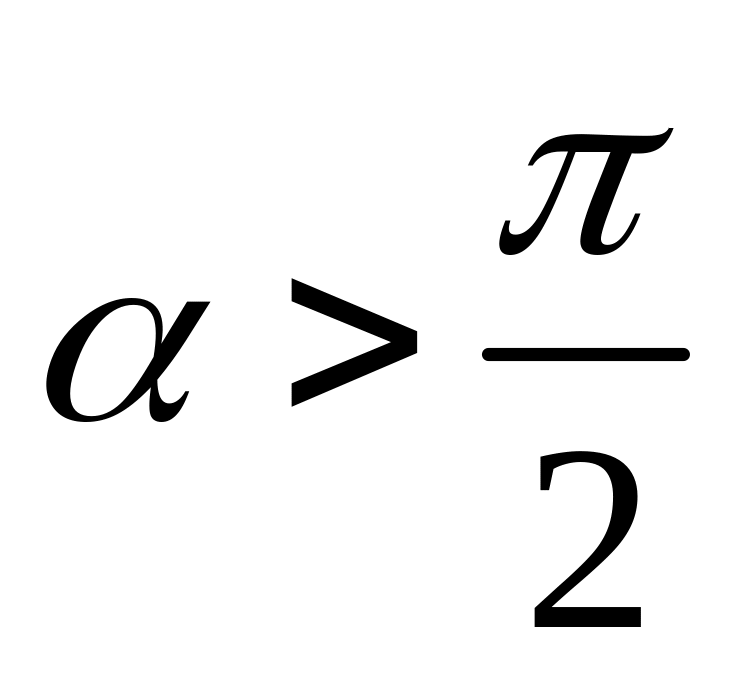то А<0(сила сопративления).
Если
,
то А=0.
Мощность – физич. величина, равная отношению работы ко времени.
,
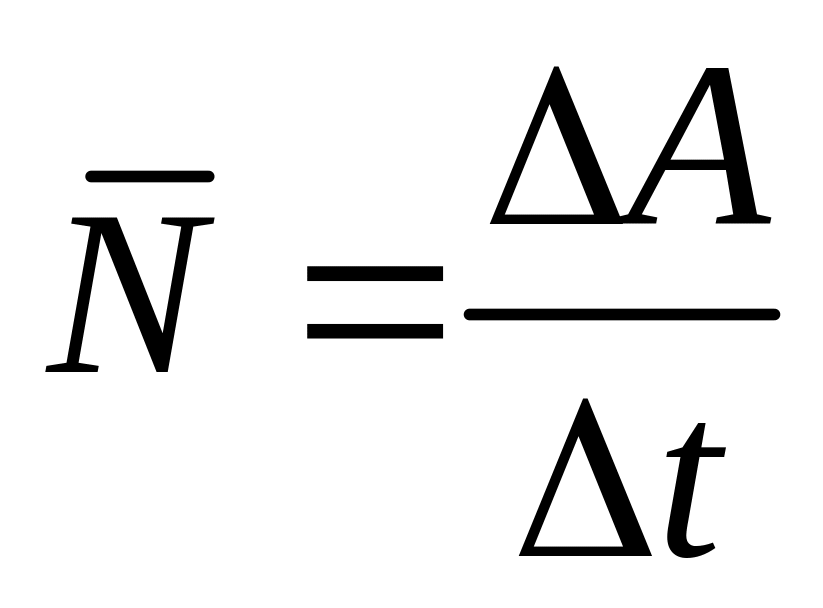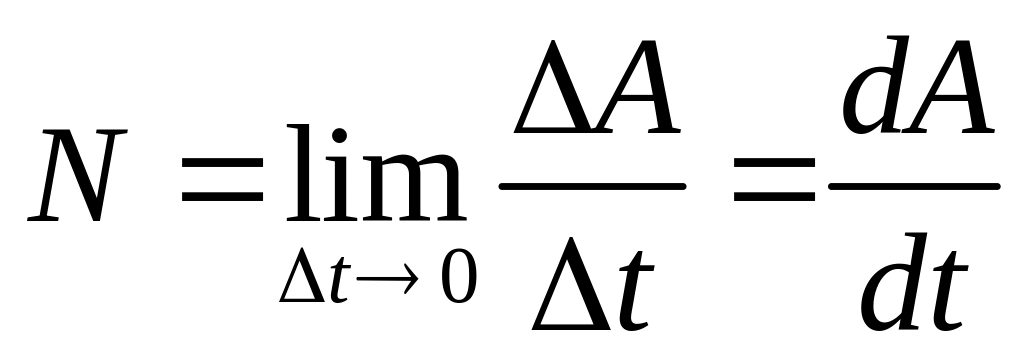- мгновенная мощность.
;
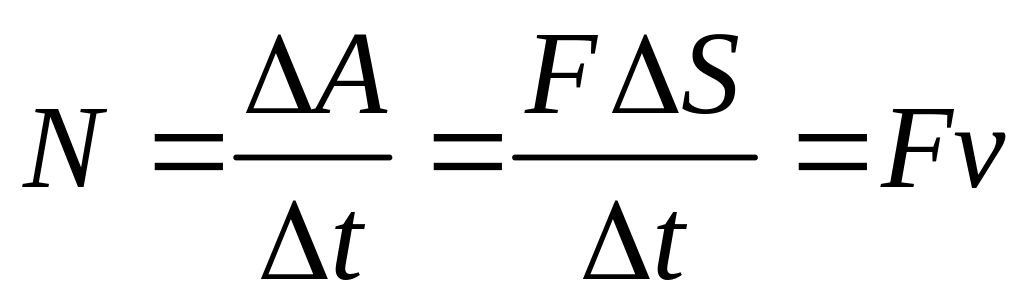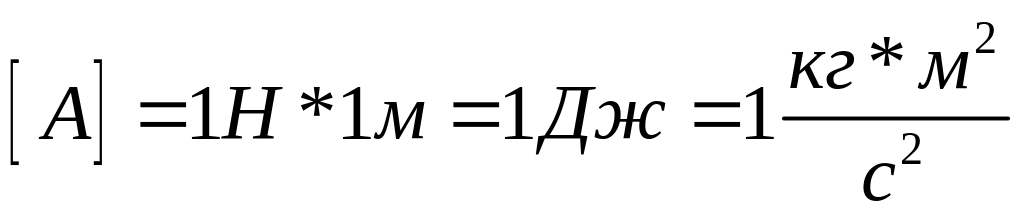
1 Дж – работа, котор. совершает сила в 1Н на пути 1м.
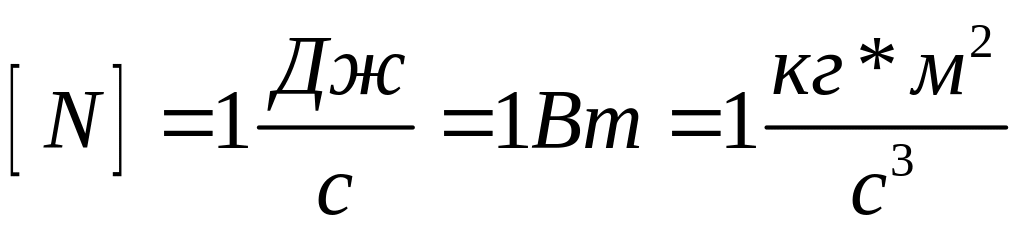
1 Вт – мощность, при котор. за время в 1с совершается работа в 1 Дж.
Кинетическая энергия (энергия движения):
,
где Т – кинетическая энергия.
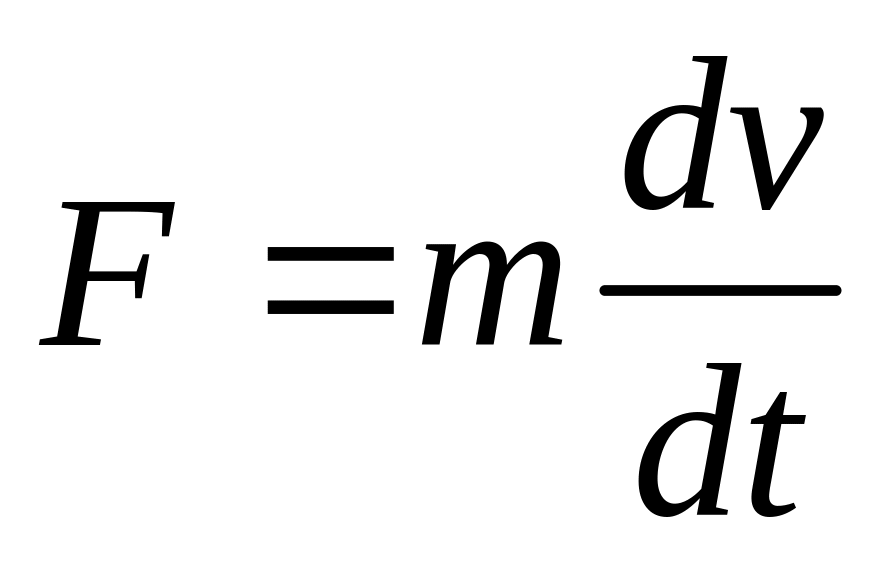(2
– ой закон Ньютона)
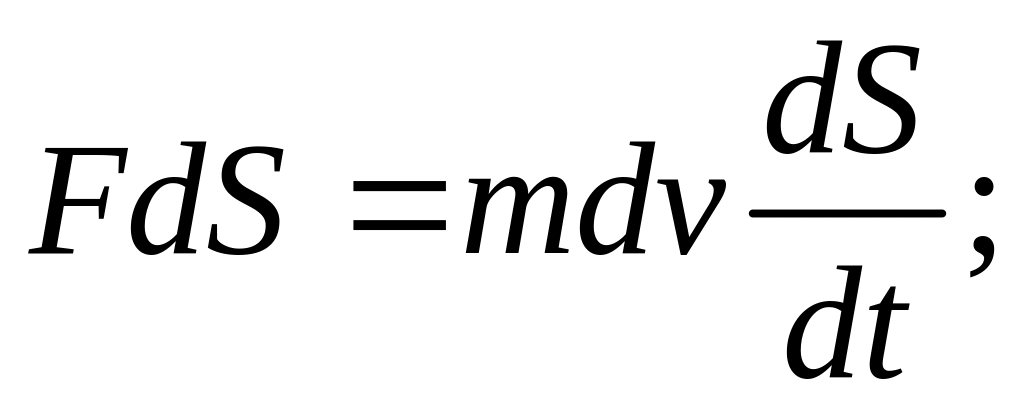
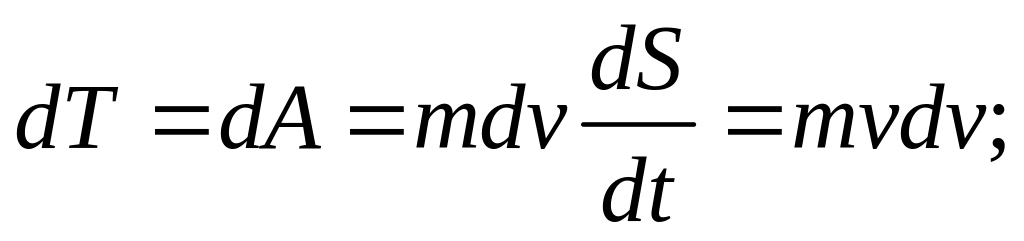
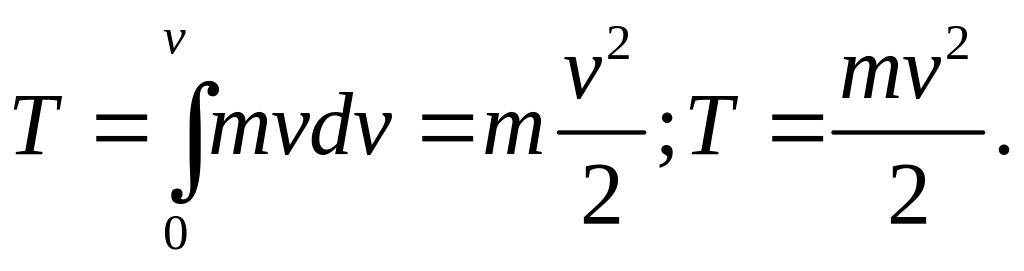
Потенциальная энергия – часть общей механической энергии системы, определ. взаимным расположением тел и характером сил взаимодействия между ними.
Пусть взаимодейст. тел осуществляется посредствам силовых полей, характеризующ. тем, что работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от пути перемещения, а зависит только от начального и конечного положений. Такие поля наз. потенциальными, а силы, действующие в них, консервативными (силы тяжести).
потенциальная
энергия (работа, выполненная консервативными
силами за счет убыли потенциальной
энергии).
;
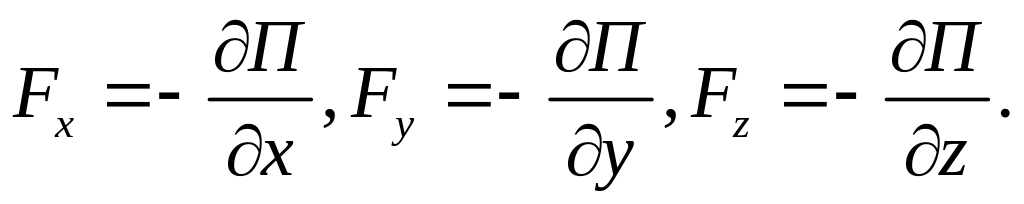
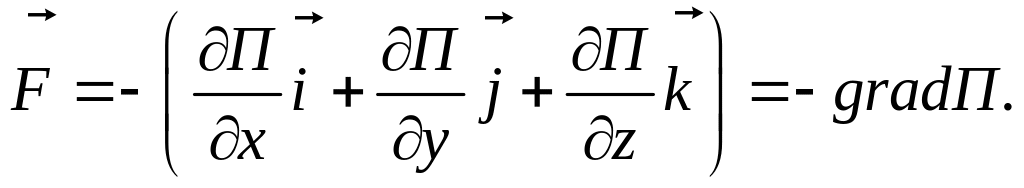
Определим потенциальные энергии упруго деформированной пружины:
,
- сила упругости;
-
абсолютная деформация;
- коэффициент
упругости.
;
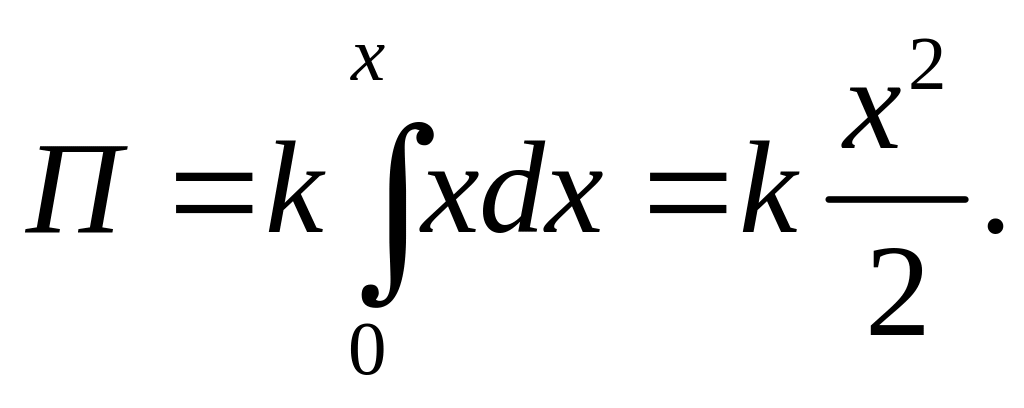
Полная механическая
энергия:
Закон сохранения энергии. Графическое представление энергии.
Пусть имеется
механическая система, состоящая из n
тел, массы
которых
и
- скорости движения.
Внутренние силы являются консервативными:
- внутренние силы;
- внешние силы.
П
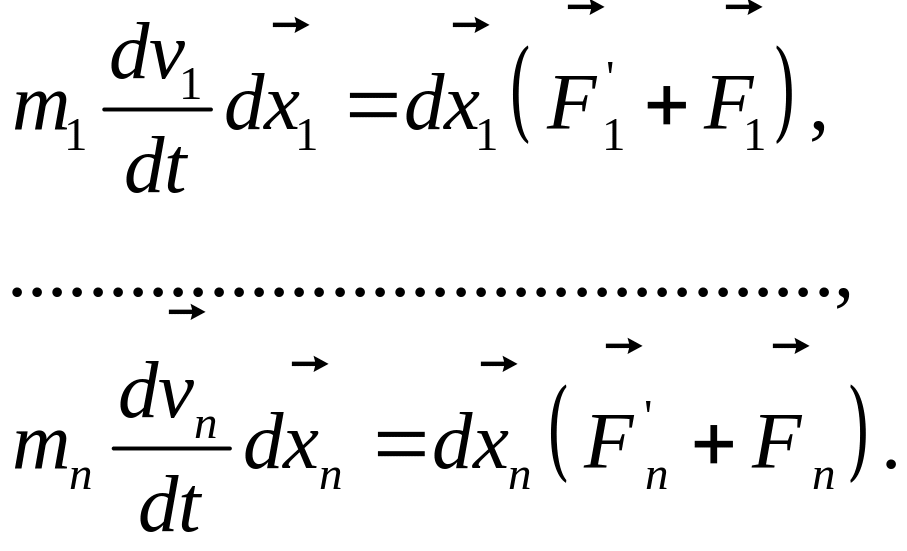усть
механическая система замкнута, тогда
2-ой закон Ньютона примет вид:
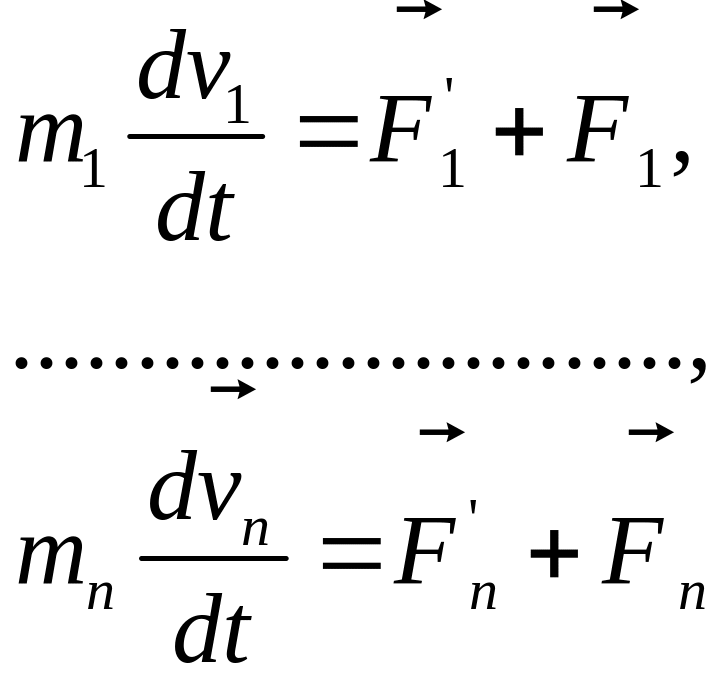
Сложим левые и
правые части, учитывая, что
.
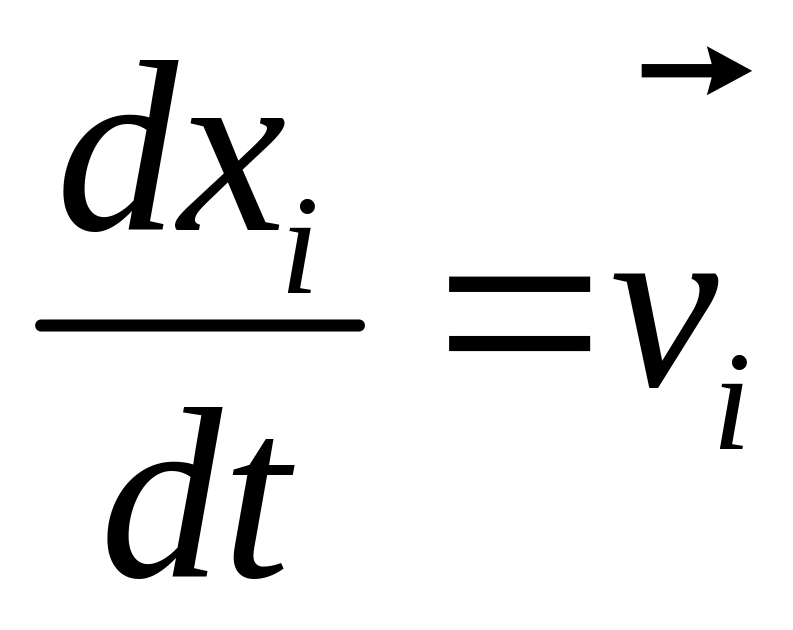Тогда
;
.
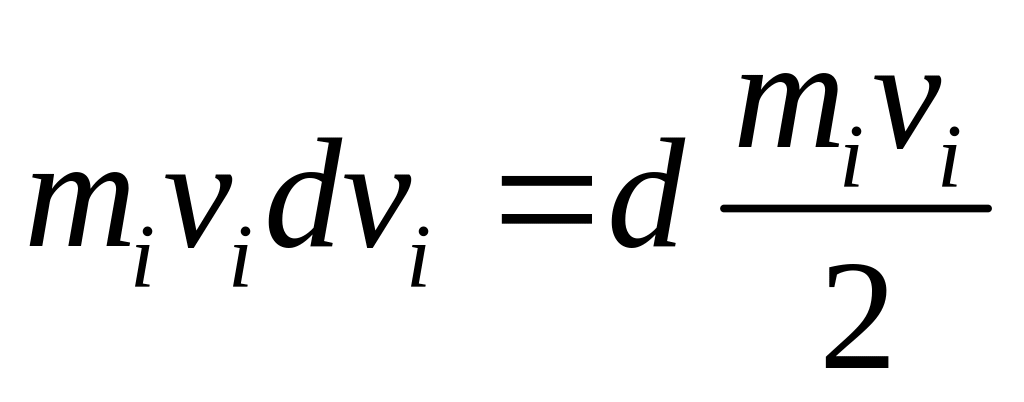т. к.
,
то
- закон
сохранения энергии.
Закон сохранения энергии:
В замкнутой механической системе, где действуют консервативные силы, механическая энергия сохраняется.
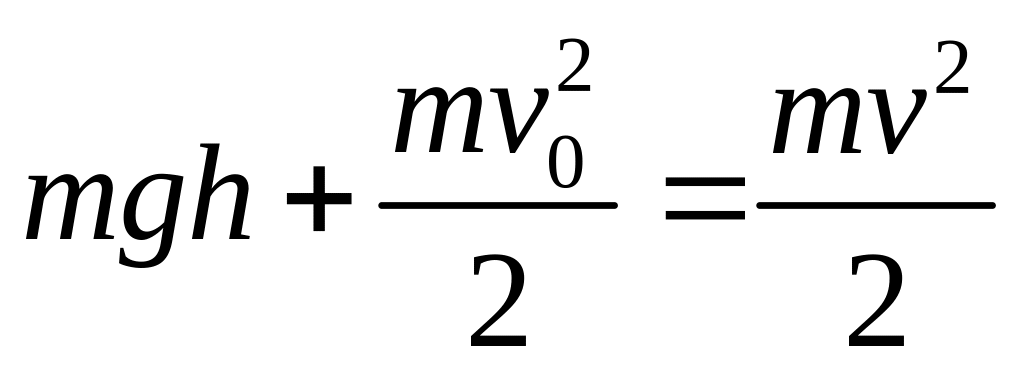
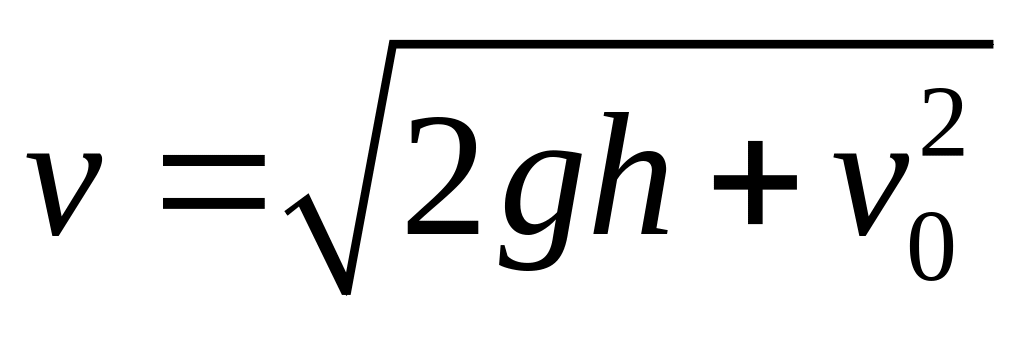
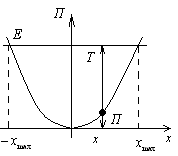
- потенциальные
кривые.
.
Пусть тело ограничено максимальной энергией.
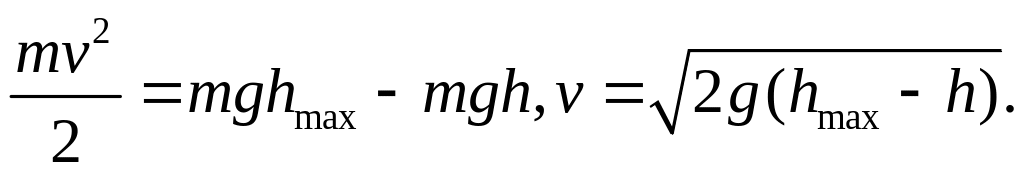
Рассмотрим тело, подвешен. на пружине:
.
-
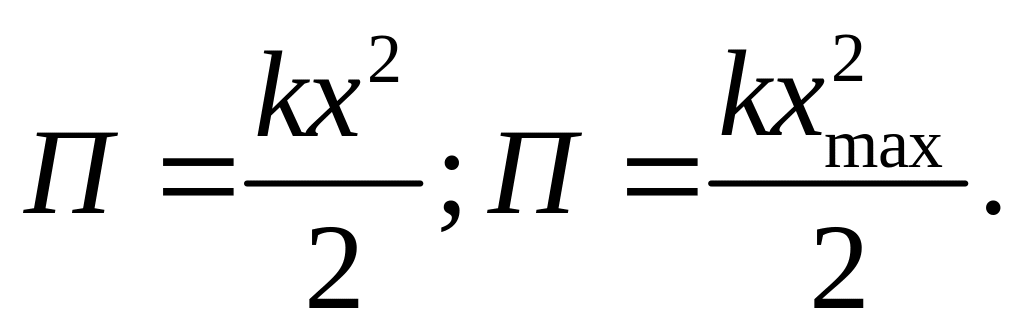
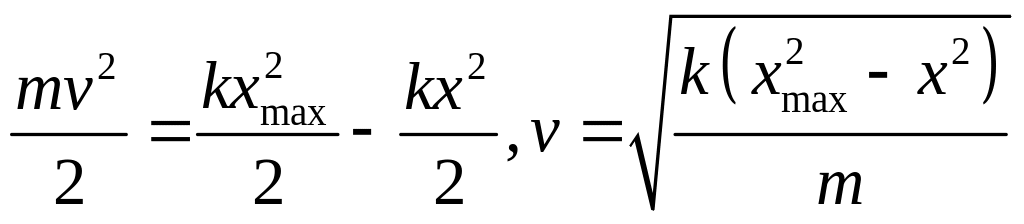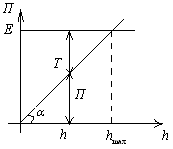
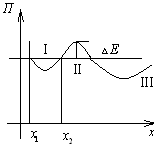высота потенциального барьера (если
добавим энергию, то тело перейдет из
в обл.
)
Если тело находится
в
или
,
то говорят, что оно находится в
потенциальной яме.
Устойчивое равновесие: система обладает минимумам потенциальной энергии.