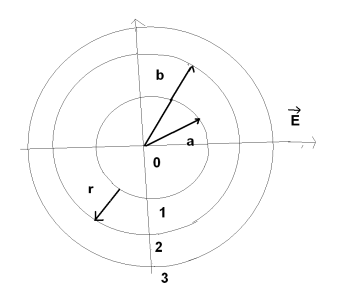
41.Потенциал в простейших электрических полях. Потенциал поля Диполя.

, , , , , , .

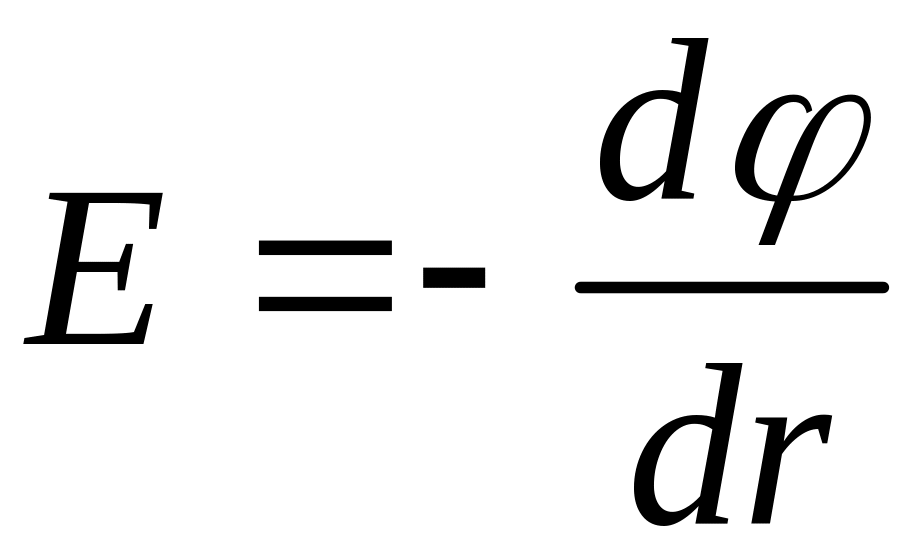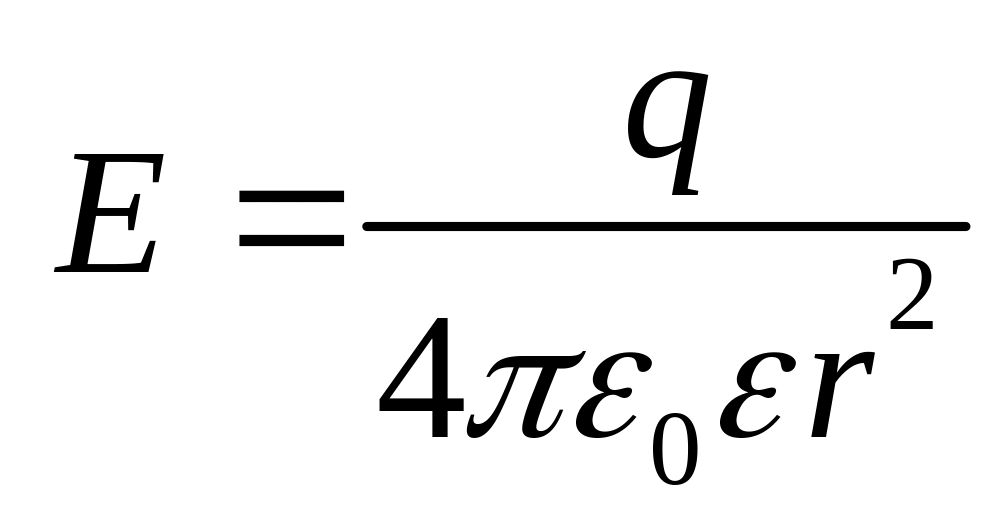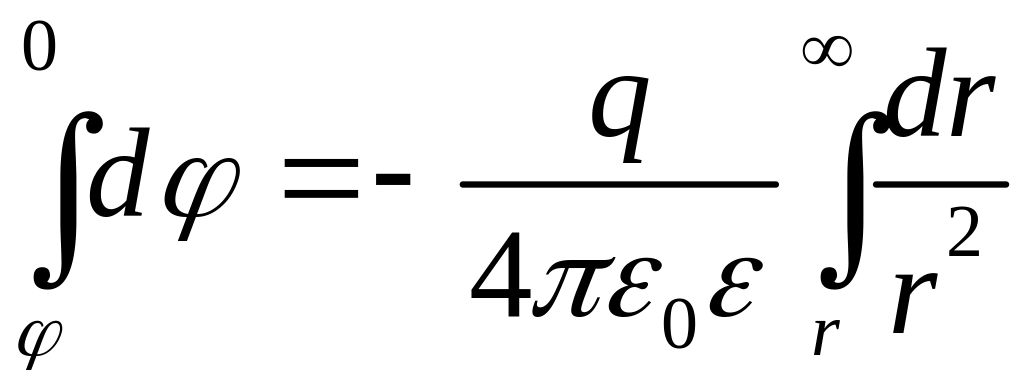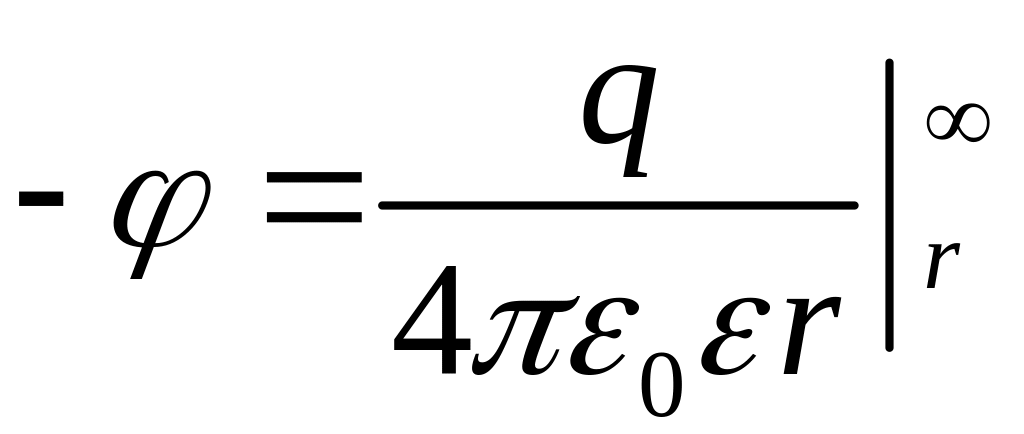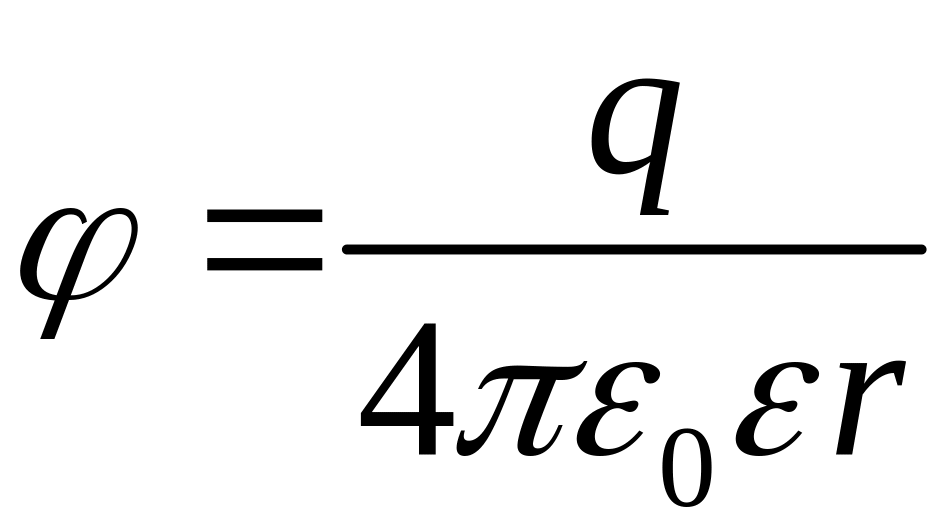Шаровой конденсатор:

, , , .

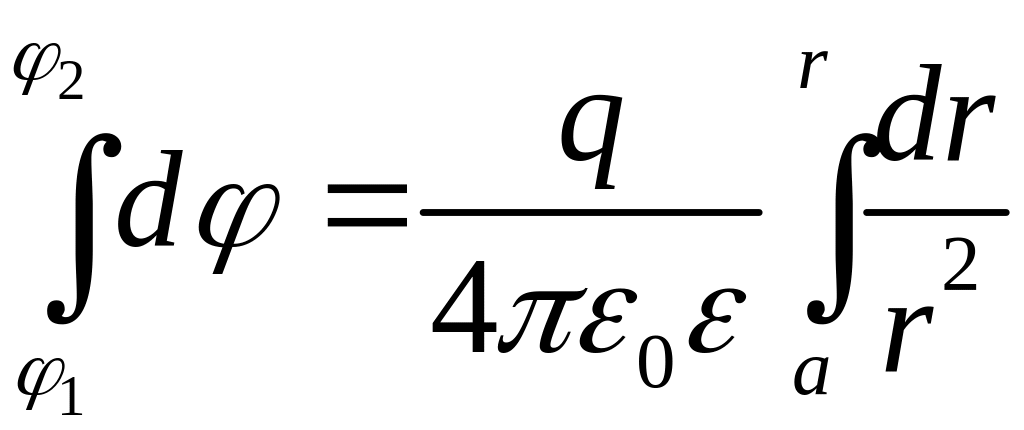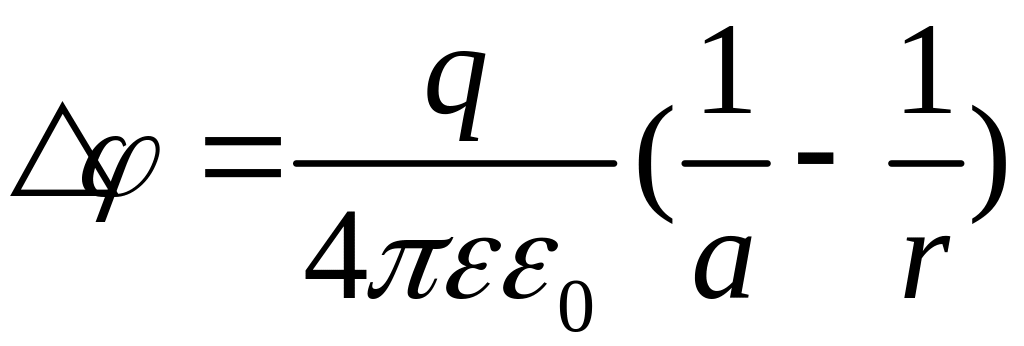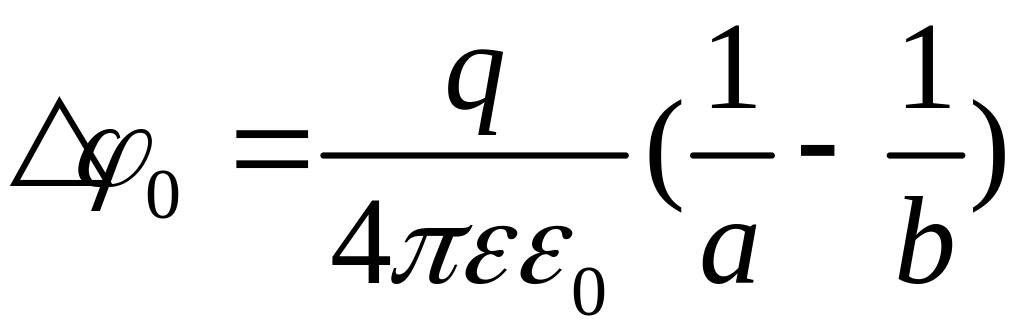Плоский конденсатор: 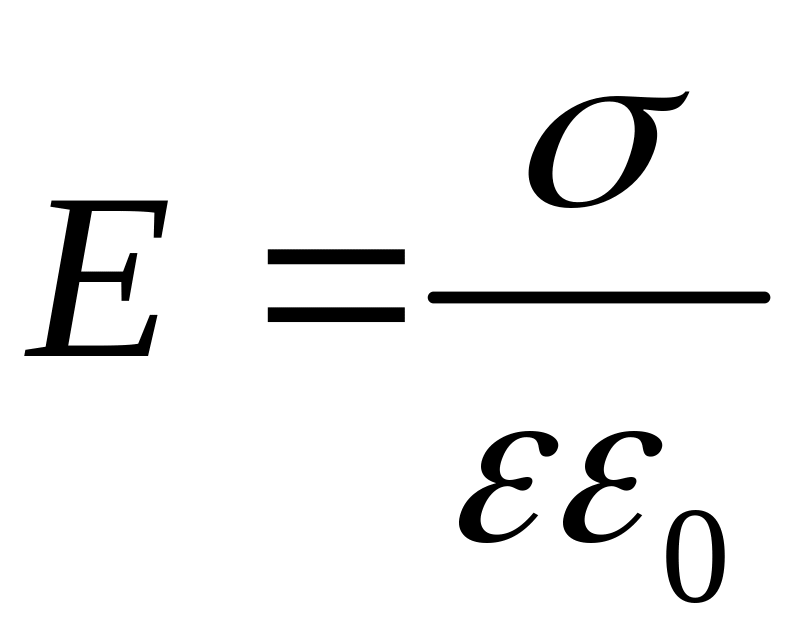, , 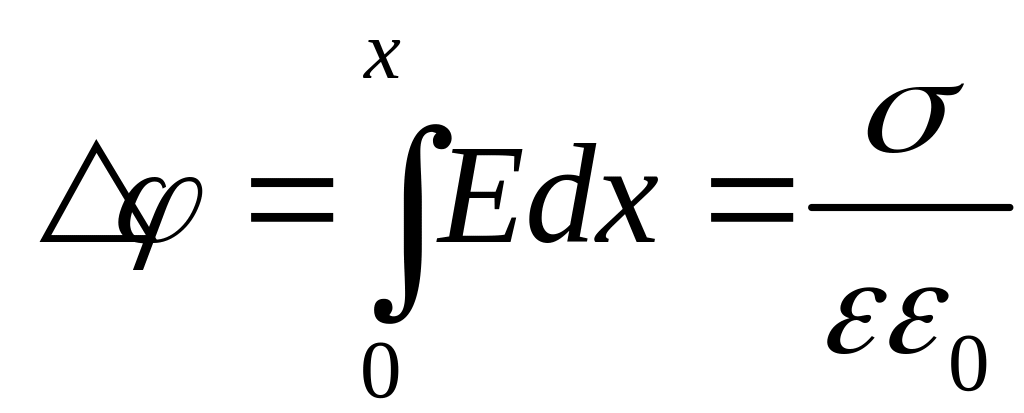, 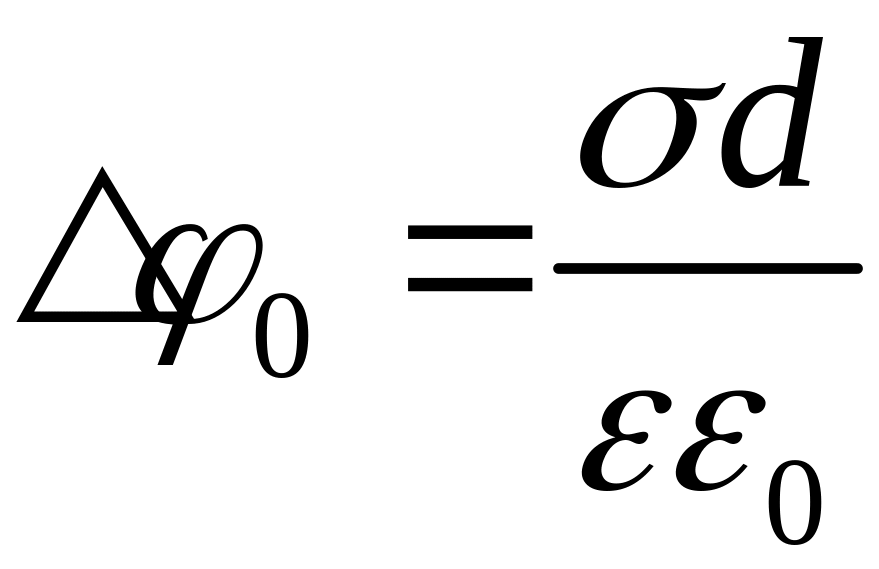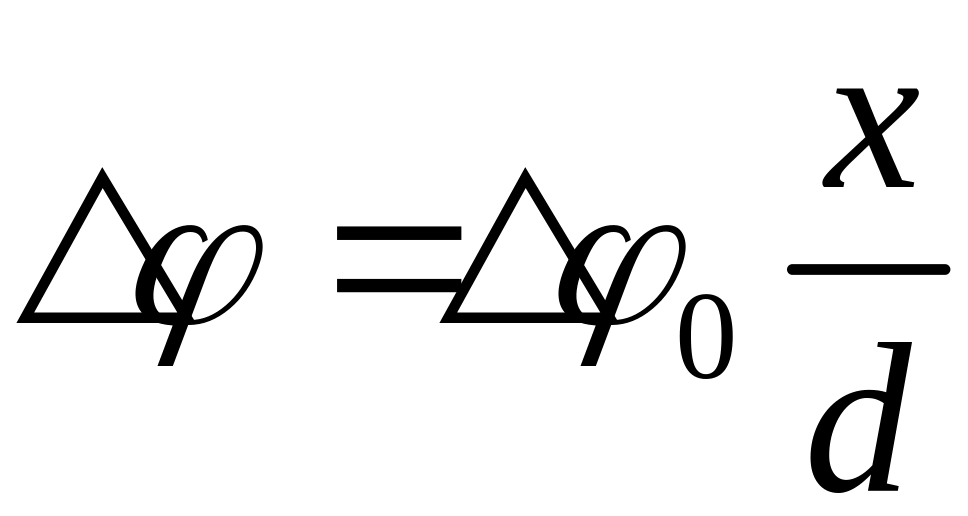.Потенциал изменяется в плоском конденсаторе по линейному закону.

Цилиндрический конденсатор: ,

, , , , , .

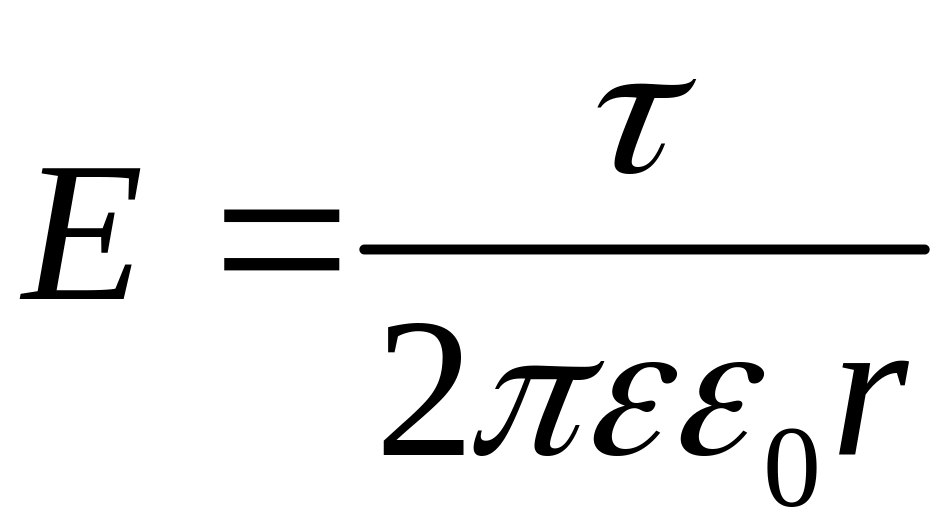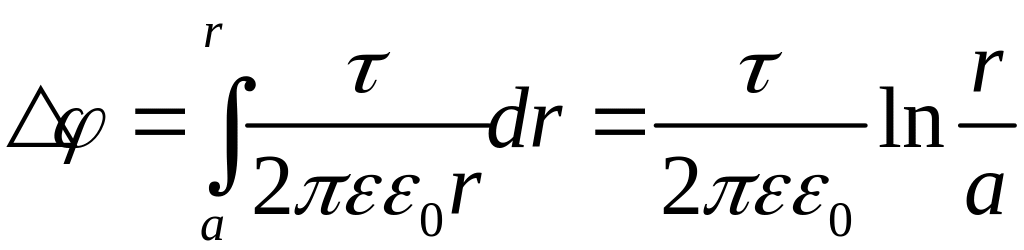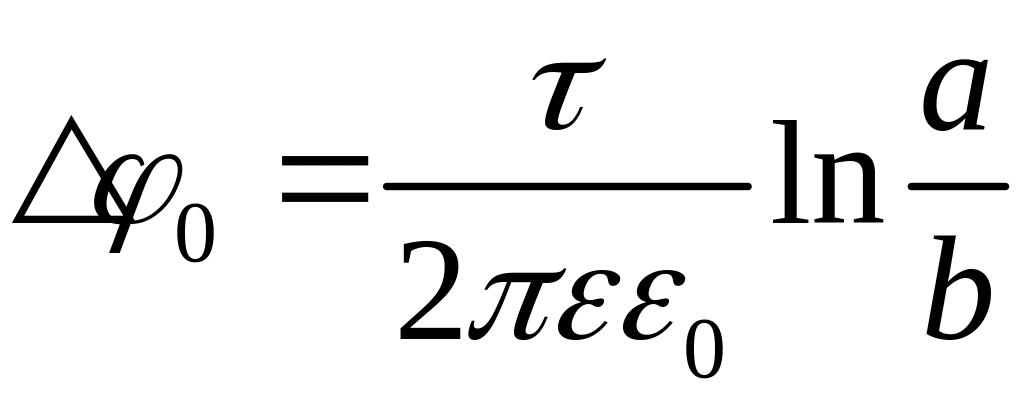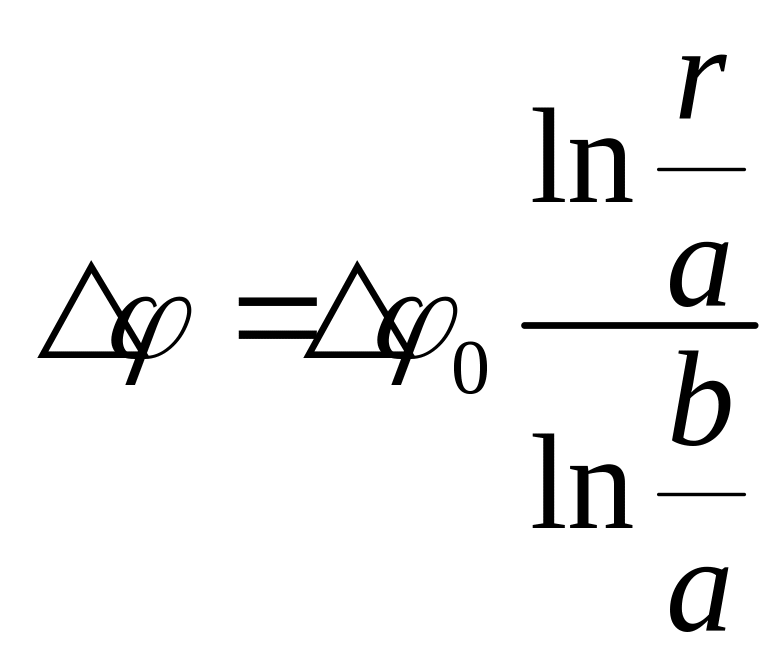
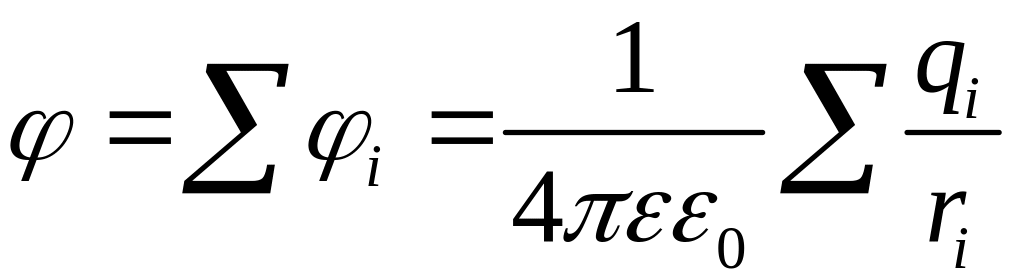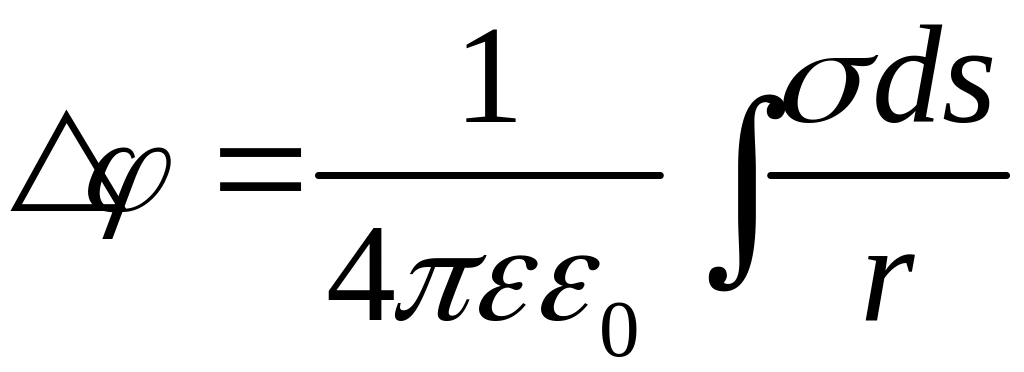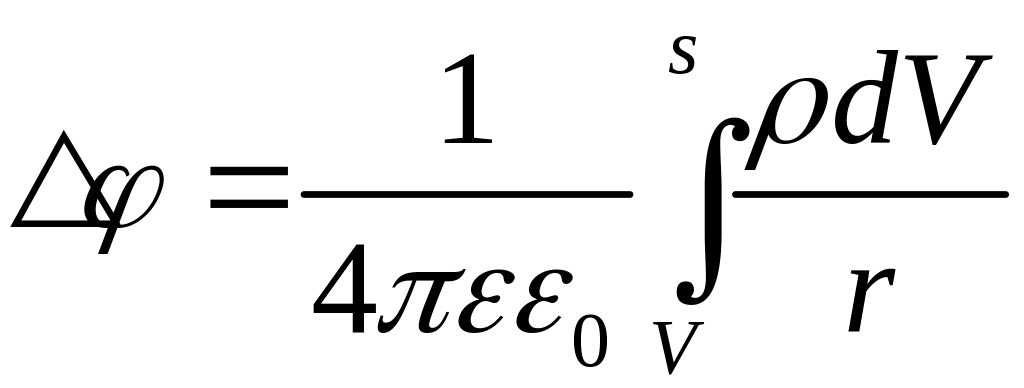Потенциал поля Диполя.

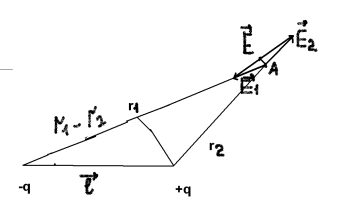
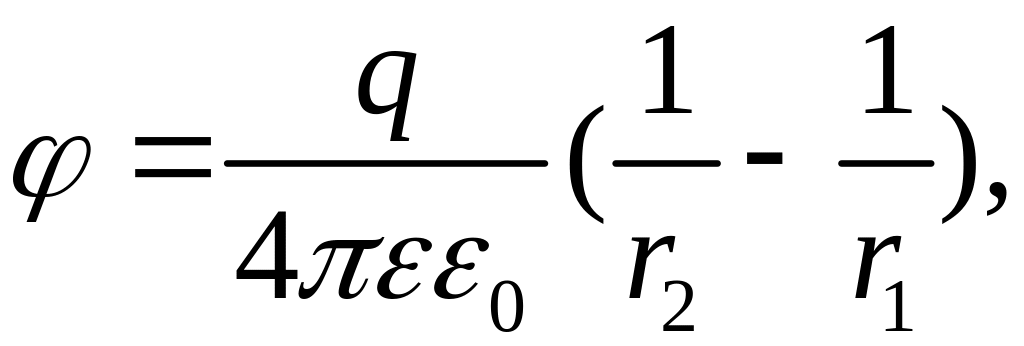
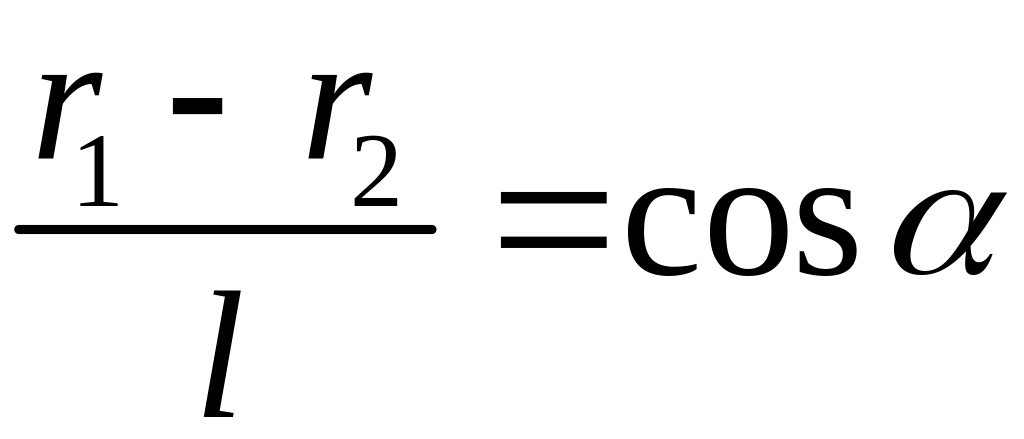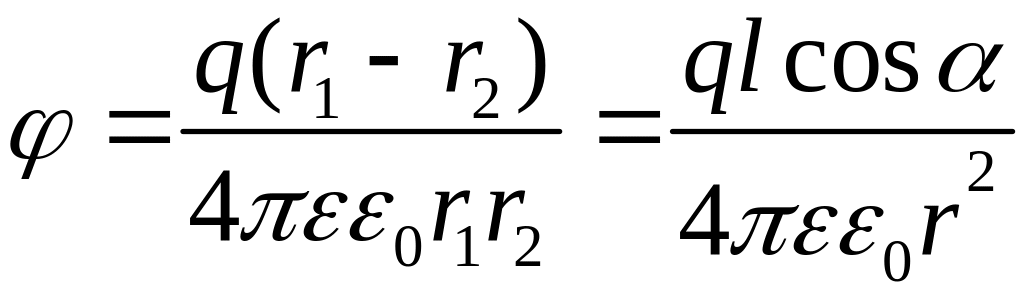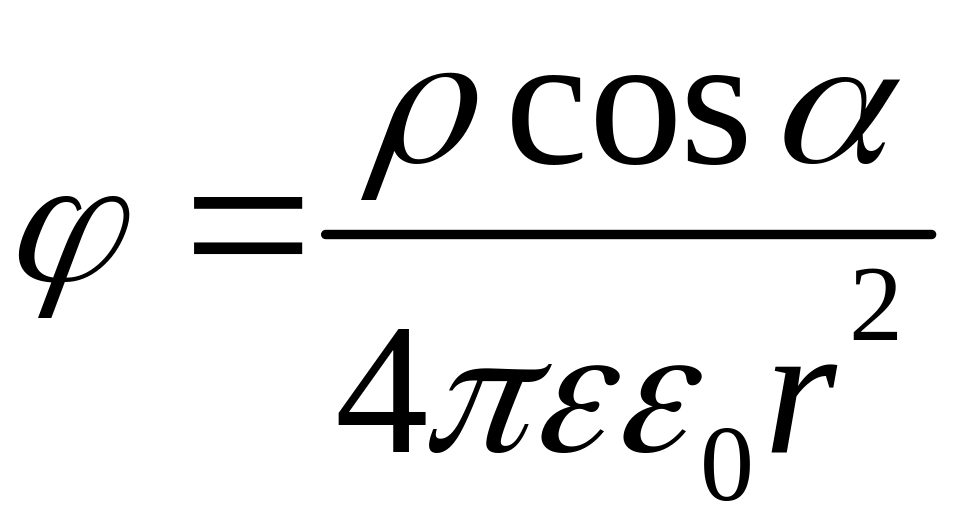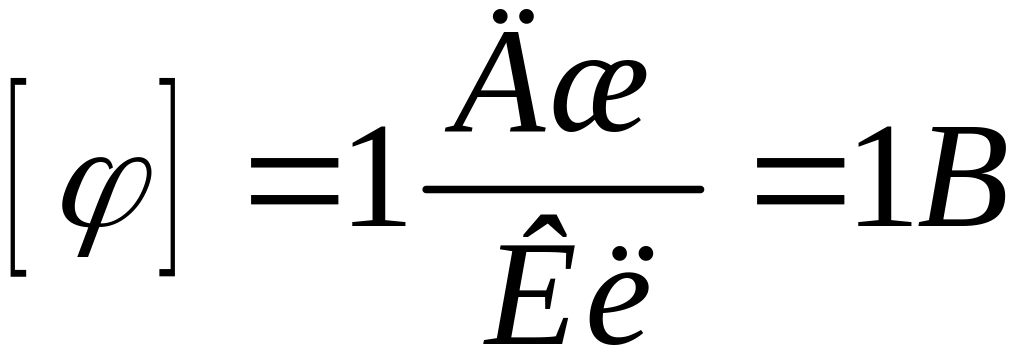, , , , , . 1 Вольт - есть потенциал такой точки поля, в которой заряд в 1Кулон обладает потенциальной энергией 1 Джоуль.

42.Электроёмкость удельного проводника.

, , -число зарядов, - потенциал.

Электроёмкость- величина, численно равная отношению заряда к величине потенциала. Она зависит от размеров проводника и формы, и не зависит от материала, агрегатного состояния, формы и размеров полостей.

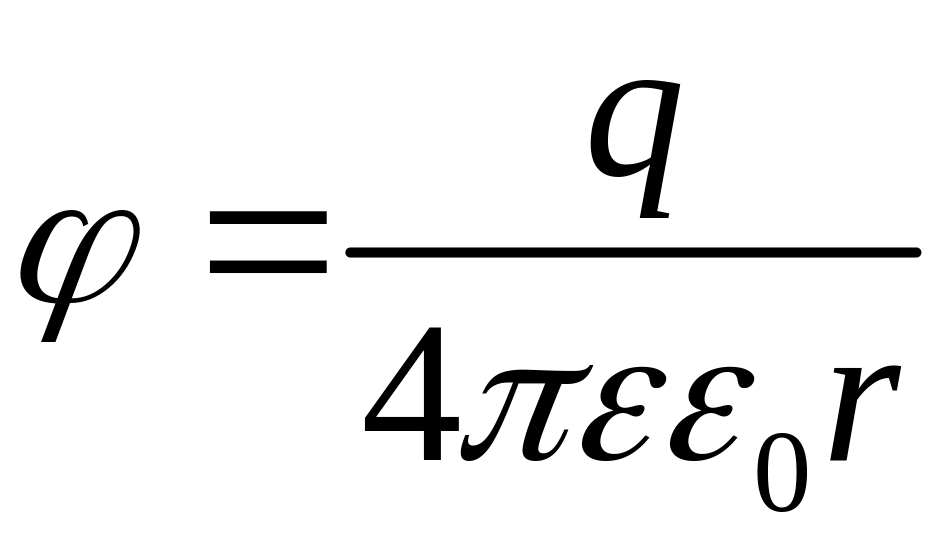. Определим шарика с ёмкостью 1Ф. , . Пусть, следовательно .

, , , .

Фарад – электроёмкость проводника, у которого изменение заряда на 1Кл изменяет измерение потенциала на 1В.

Электроёмкость простых конденсаторов: плоский, шаровой, цилиндрический.

Плоский конденсатор: , ,

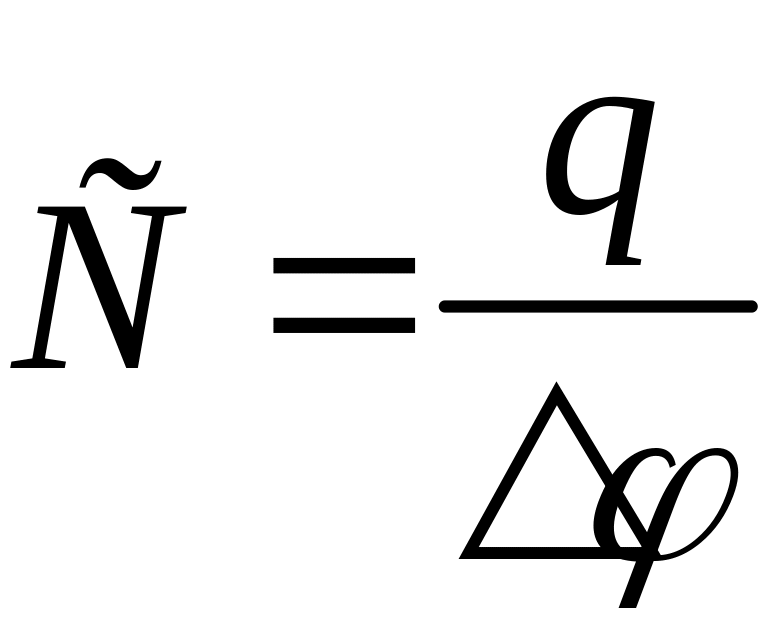-площадь пластинки. , .

, , .

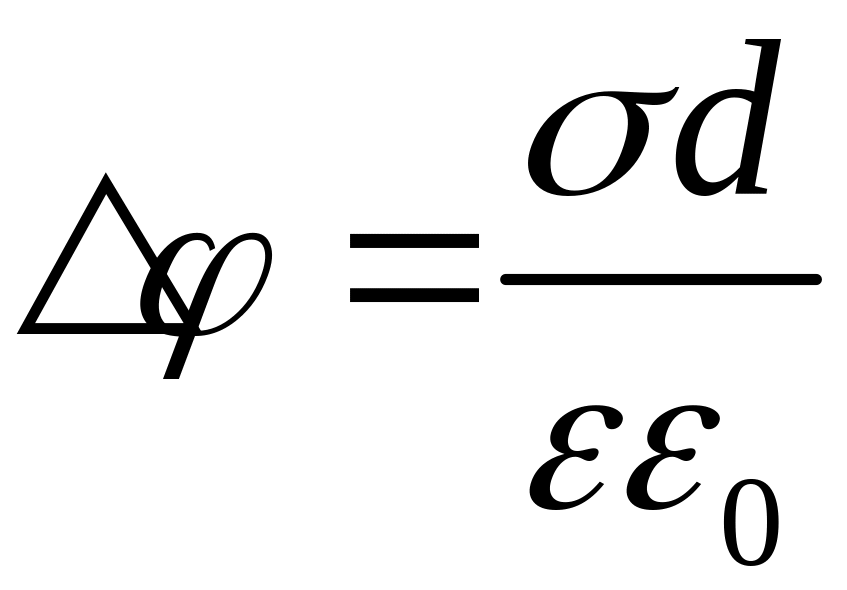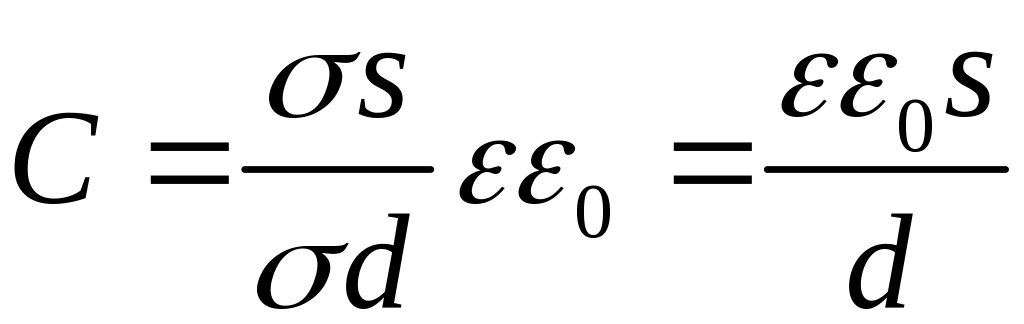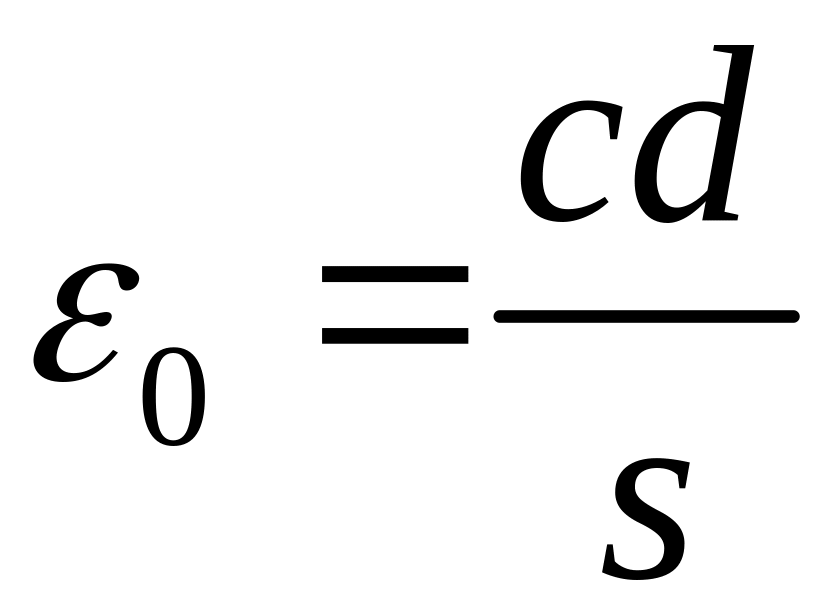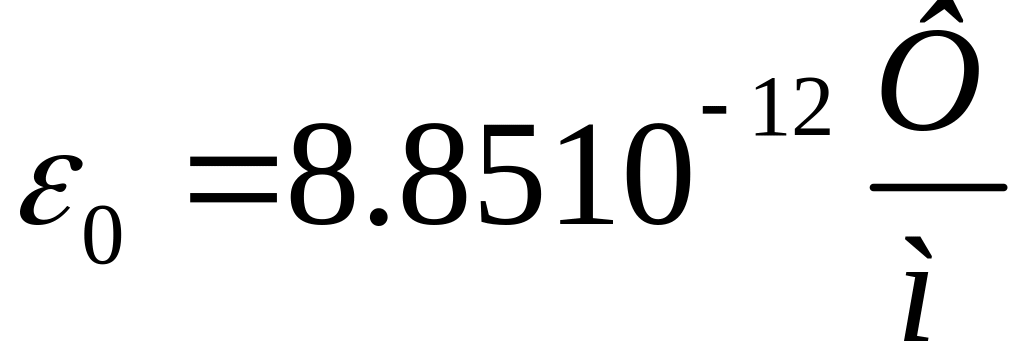Шаровой конденсатор: ,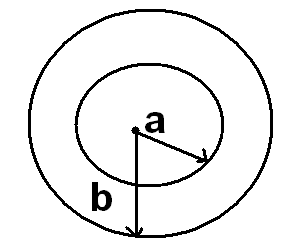

. , . , ,

. , , , .

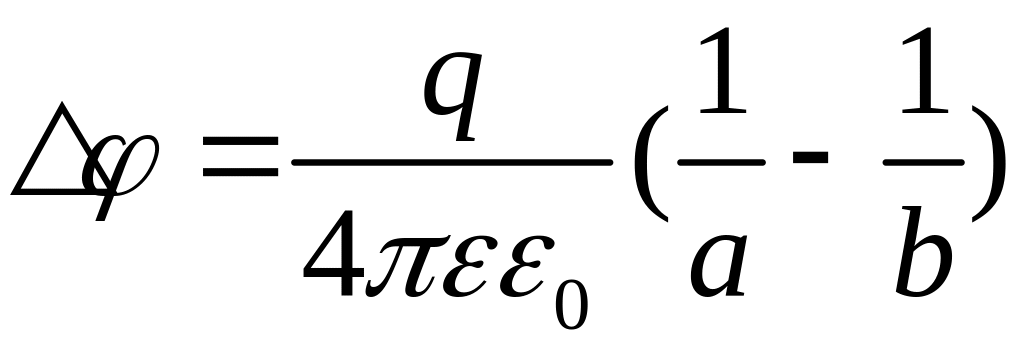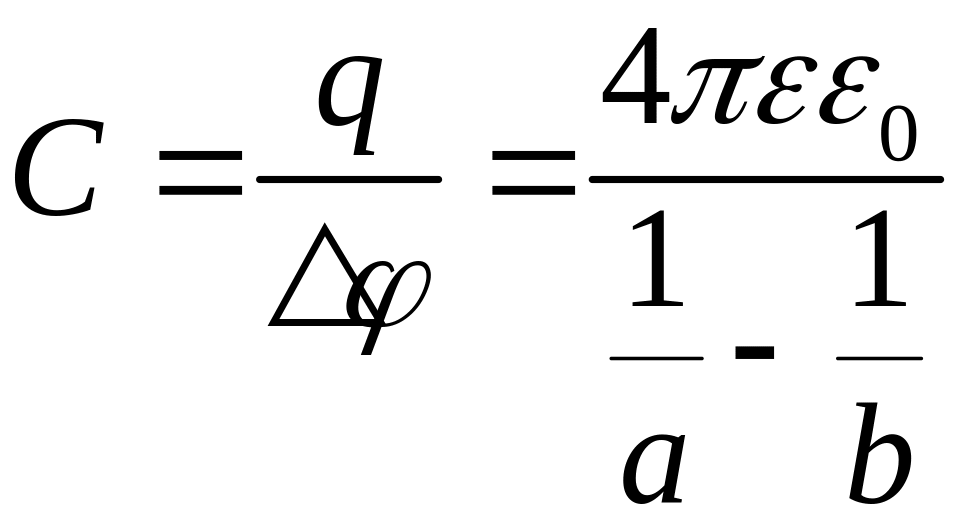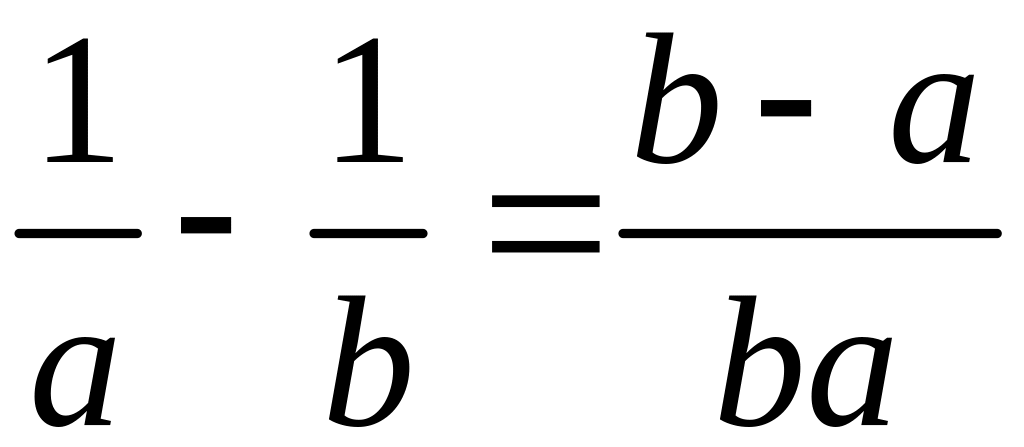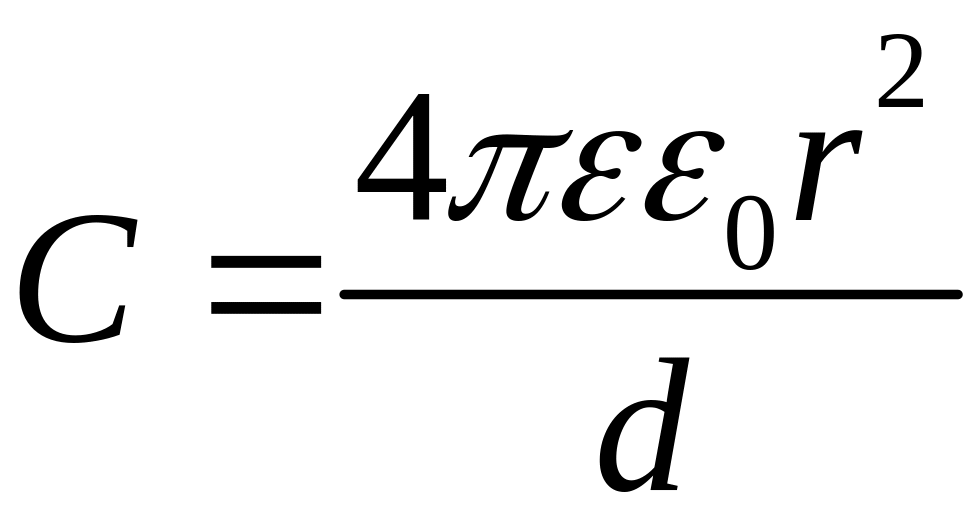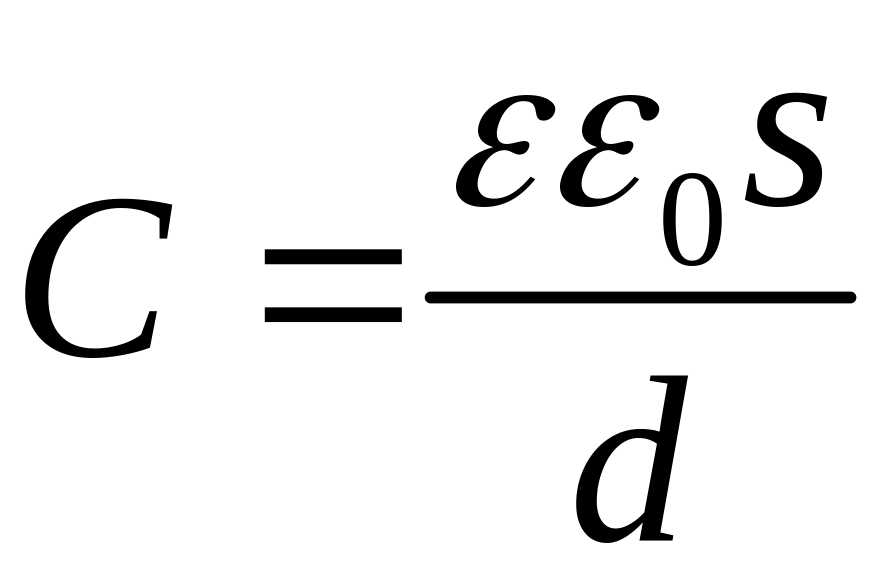Цилиндрический конденсатор: , , , , .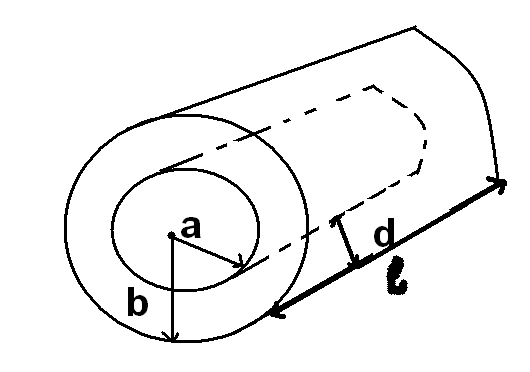

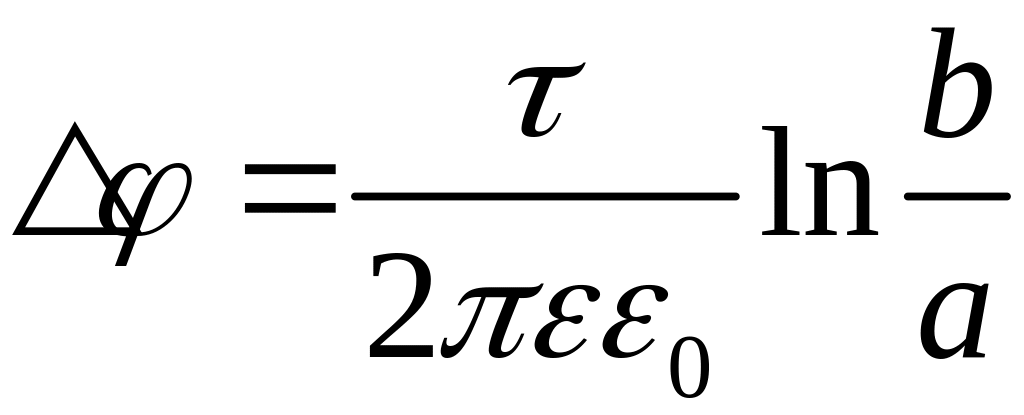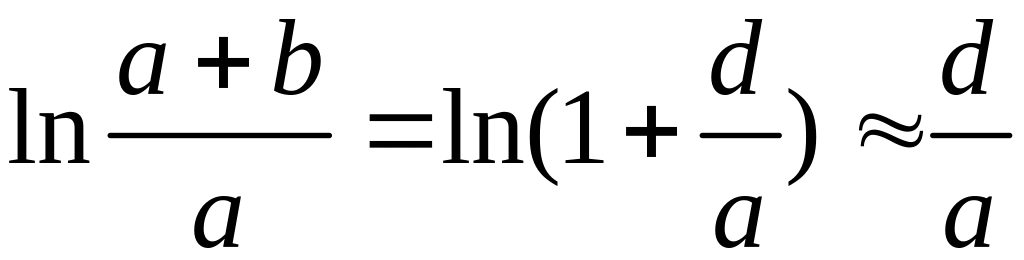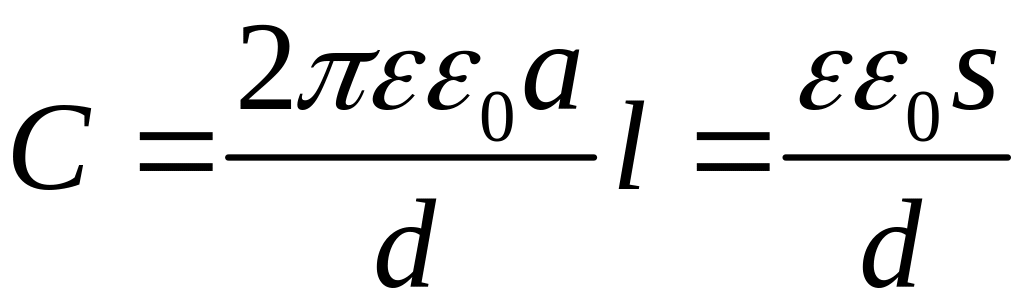Соединение конденсаторов: параллельное, последовательное, смешенное.

Параллельное: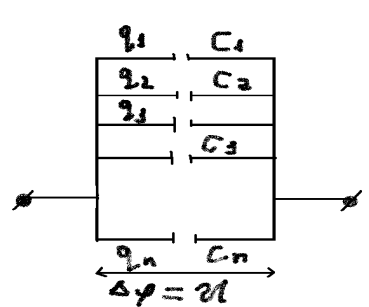 При параллельном соединении разность потенциалов (напряжение) на всех конденсаторах одинакова, а величина заряда равна сумме зарядов, находящихся на каждом конденсаторе.

, , , , .

Последовательное: , , , .

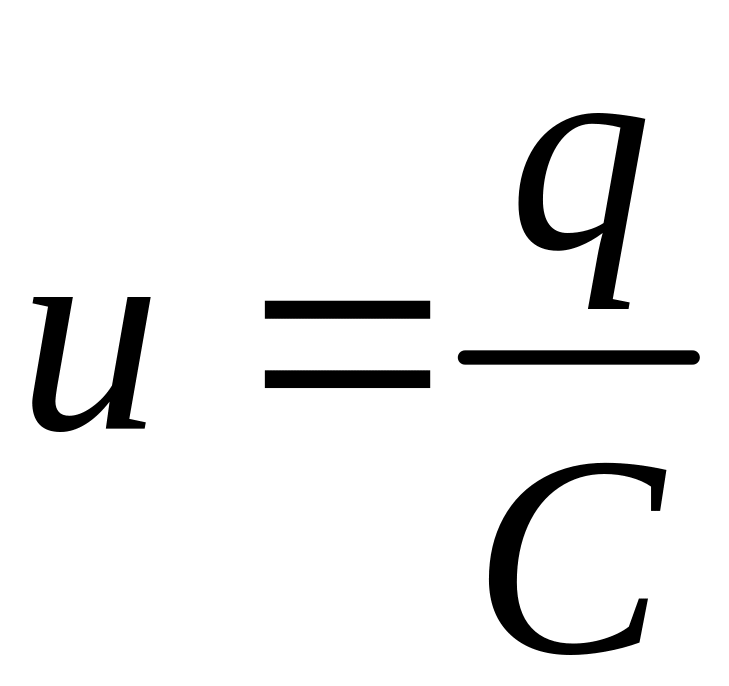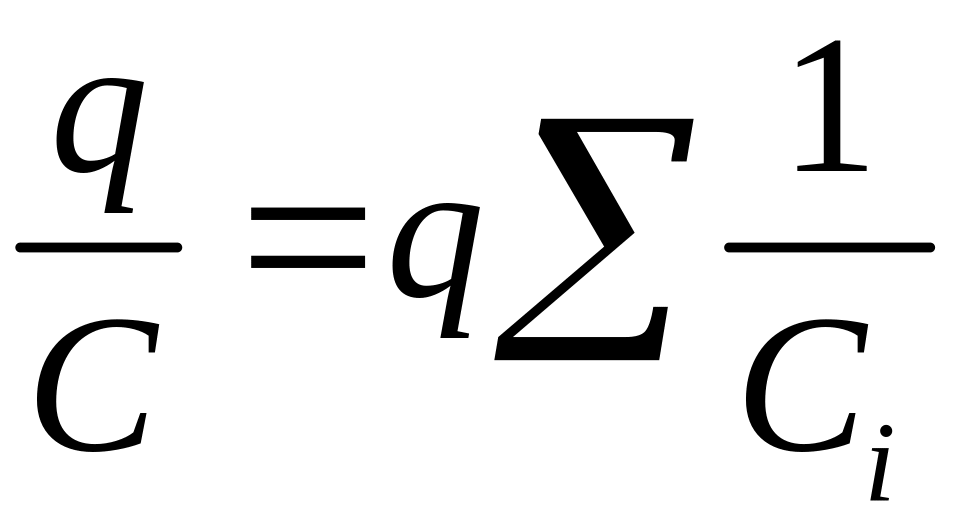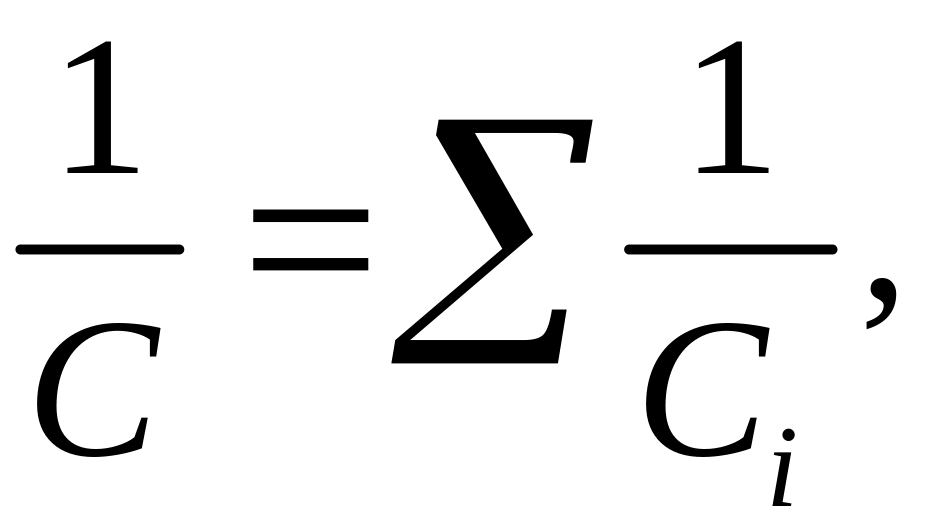
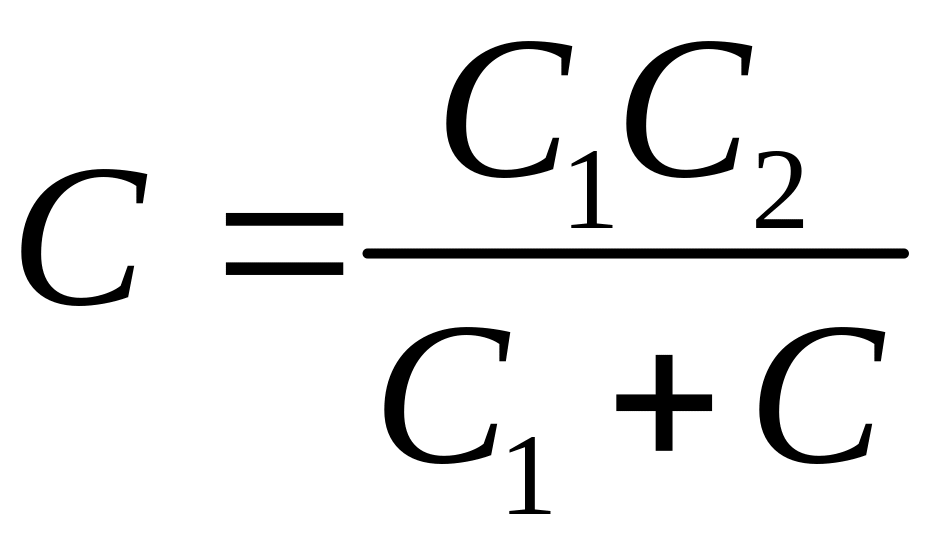Смешенное: ,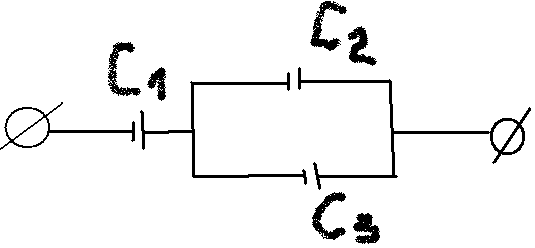

, .

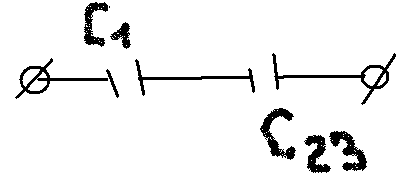
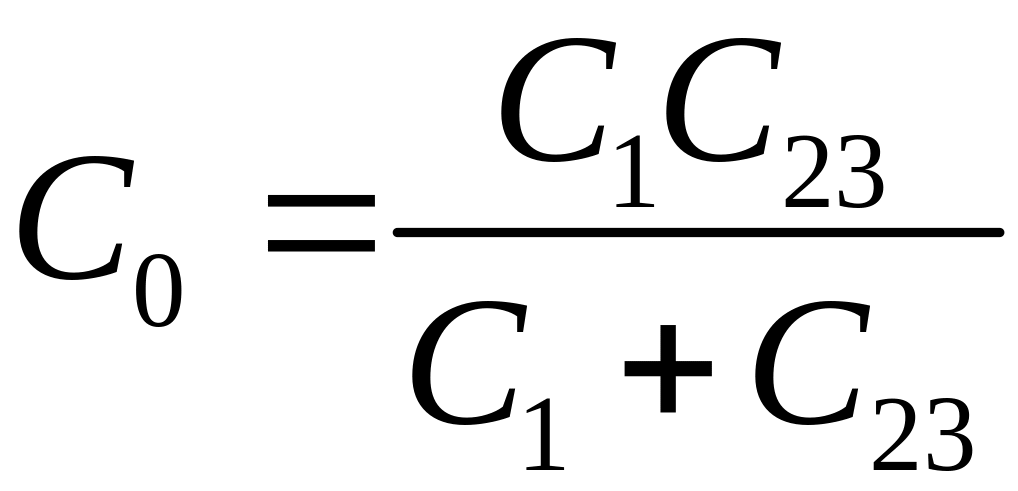43.Энергия уединенного заряженного проводника.

Для совокупности многих зарядов потенциальная энергия вычисляется как полу сумма произведения каждого заряда на сумму потенциалов полей, созданных всеми зарядами кроме него самого: умножится на сумму всех потенциалов кроме и т.д. Причина в том, что поле, созданное некоторым неподвижным зарядом , действует на любые другие заряды, но не на этот заряд

Э нергия заряженного конденсатора.

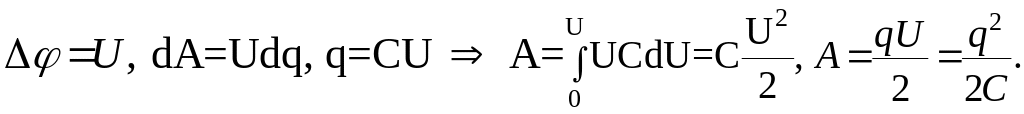
Знак «-» показывает, что сила стремится уменьшить расстояние между пластинами, т.е. является силой притяжения.

Энергия электростатического поля.

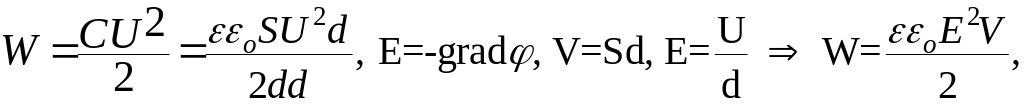где V- объем конденсатора. Последняя формула показывает, что энергия конденсатора выражается через величину, характеризующую электростатическое поле, - напряженность Е. Объемная плотность энергии электростатического поля (энергия единицы объема)

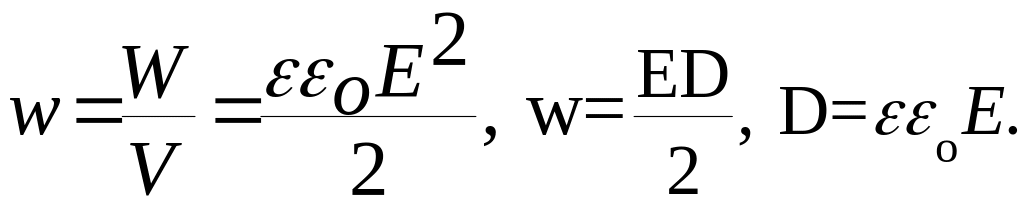
44. Характеристики электрического тока: сила и плотность тока. Ток – направленное движение заряженных частиц. Природа эл. тока в металлах и в полупроводниках: движущиеся электроды; в растворах – направленное движение положительных и отрицательных ионов; газы – направленное движение электронов и ионов. За направление эл. тока выбрано направление движения положительно заряженных частиц. Силой тока называют заряд, прошедший через полное сечение проводника за единицу 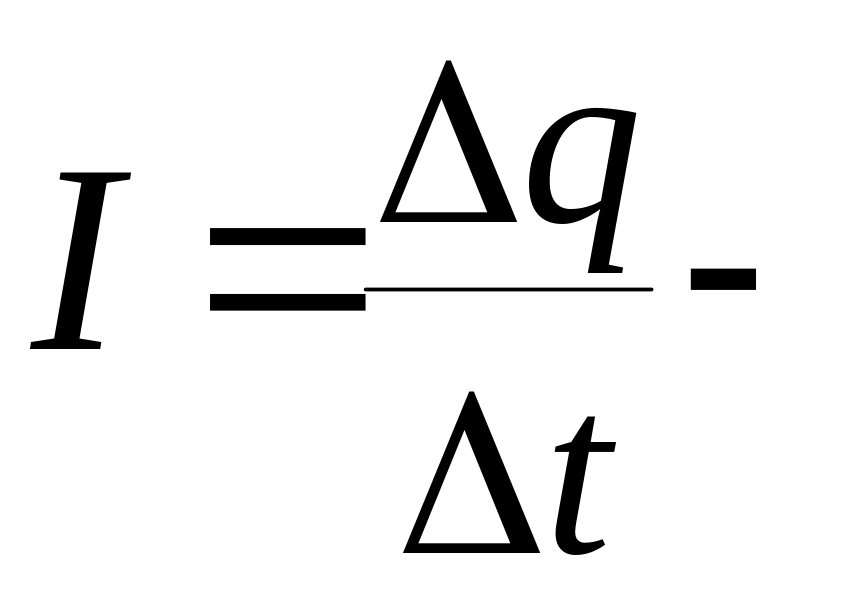времени. величина скалярная. Если за равные промежутки времени через проводник п роходят равные заряды и направление тока при этом не изменяется со временем, то такой ток наз. постоянным. Плотность тока равна величине заряда, прошедшего в единицу времени через единицу площади п ерпендикулярной линиям тока.

1А – сила тока, при котором через полное сечение проводника проходит заряд равный 1Кл за время 1с.

45.Сторонние силы. Электродвижущая сила (ЭДС) и напряжение. Физическая величина, определяемая работой, совершаемой сторонними силами при перемещении единичного положительного заряда, наз. ЭДС действующей в цепи.

ЭДС, действующая в замкнутой цепи, определяется как циркуляция вектора напряженности.

.

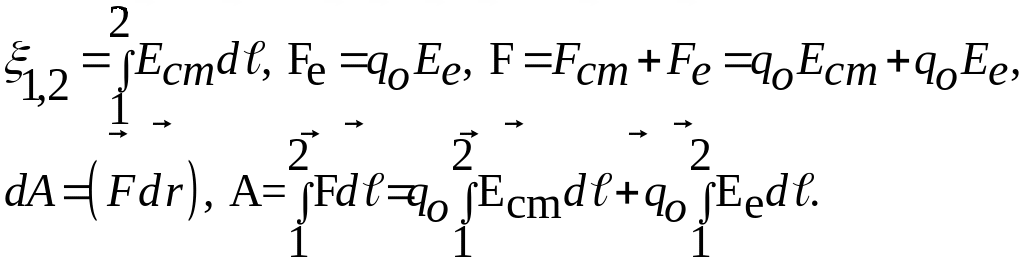
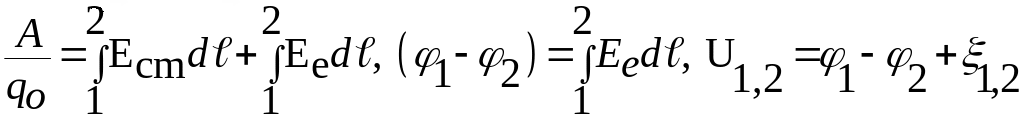Напряжение на участке цепи 1,2 наз. величина, определяемая работой, совершаемой суммарным полем электростатических и сторонних сил при перемещении единичного положительного заряда на данном участке цепи. Понятие напряжения является обобщением понятия разности потенциалов: напряжение на концах участка цепи равно разности потенциалов в том случае, если на этом участке цепи не приложена ЭДС, т.е. сторонние силы отсутствуют. Участок цепи, содержащий ЭДС, называется нелинейным.

46. З-н Ома для однородного участка цепи. Сопротивление проводников. Последовательное и параллельное подсоединение. Немецкий физик Г. Ом (1787-1854) экспериментально установил, что сила тока текущего по однородному металлическому проводнику (т.е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению на концах проводника: (закон Ома для участка цепи), где – эл. сопротивление проводника. 1 Ом –сопротивление такого проводника, в котором при напряжении 1 В течет постоянный ток 1 А. Величина наз. электрической проводимостью. Единица проводимости – сименс. 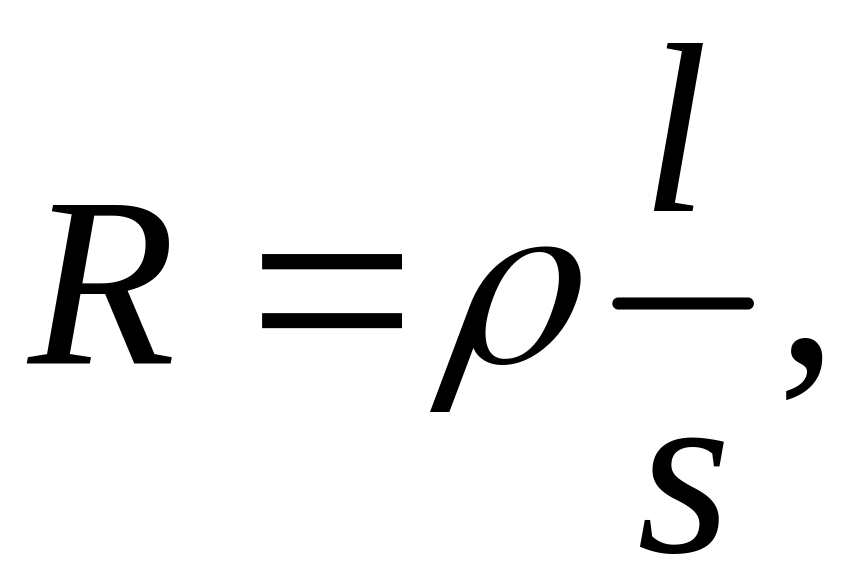Для однородного линейного проводника сопротивление R прямо пропорционально его длине и обратно пропорционально площади его поперечного сечения S: – удельное сопротивление проводника. - длина проводника, S –площадь поперечного сечения. Ед. удельного сопротивления – ом-метр (Ом·м). Последовательное соединение сопротивлений: 1) При последовательном соединении сопротивлений сила тока во всех участках цепи одинакова 2) при посл. соединении сопротивлений, напряжение на внешней цепи равно сумме напряжений на отдельных участках цепи 3) Напряжение на отдельных участках цепи при последовательном соединении прямо пропорционально сопротивлению участка 4) При посл. соединен. сопротив. эквивалентное сопротивление всей цепи равно сумме сопротивлений отдельных участков цепи для всех . Параллельное соединение сопротивлений: 1) При параллельном соединений напряжение на отдельных ветвях и на всем соединении одинаково 2) ток до и после разветвления равен сумме токов в отдельных ветвях 3) ток в отдельных разветвлениях обратно пропорционально сопротивлениям этих ветвей 4) Проводимость всего ветвления равна сумме проводимостей отдельных ветвей 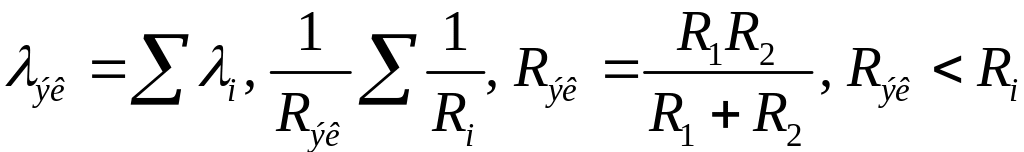для всех .

Зависимость сопротивления от температуры.

Рассмотрим формулы: где и и – соответственно удельное сопротивления и сопротивления проводника при и – температурный коэффициент сопротивления, для чистых металлов (при не очень низких температурах) близкий к 1/123 К^-1. Следовательно, температурная зависимость сопротивления может быть представлена в виде где –термодинамическая температура. Сопротивление многих металлов (например, ) и их сплавов при очень низких температурах (0,14 -20К), называемых критическими, характерных для каждого вещества, скачкообразно уменьшается до нуля, т.е. металл становится абсолютным проводником. Впервые это явление, названное сверхпроводимостью, обнаружено в 1911 г. Г.Камерлинг-Оннесом для ртути. Явление сверхпроводимости объясняется на основе квантовой теории. Практическое использование сверхпроводящих материалов затруднено из-за их низких критических температур. В настоящее время обнаружены и активно исследуются керамические материалы, обладающие сверхпроводимостью при температуре выше 100К. На зависимости электрического сопротивления металлов от температуры основано действие термометров сопротивления, которые позволяют по градуированной взаимосвязи сопротивления от температуры измерять температуру с точностью до 0,003 К. Термометры сопротивления, в которых в качестве рабочего вещества используются полупроводники, изготовленные по специальной технологии, называются термисторами. Они позволяют измерять температуры с точностью до миллионных долей кельвин.

47. З-н Ома в дифференциальной форме для неоднородного участка цепи.

Рассмотрим неоднородный участок цепи. Обозначим э.д.с. через а разность потенциалов – Если ток проходит по неподвижным проводникам, то работа А всех сил, совершаемая над носителем тока, по закону сохранения и превращения энергии равна теплоте, выделяющееся на участке. Работа всех сил, совершаемая при перемещении заряда на участке: Э.д.с. как и сила тока – величина скалярная. Ее необходимо брать либо с положительным, либо с отрицательным знаком в зависимости от знака работы, совершаемой сторонними силами. За время в проводнике выделяется теплота Из формул и получим откуда это выражение представляет собой закон Ома для неоднородного участка цепи, который является обобщенным законом Ома. Если на данном участке цепи источник тока отсутствует то приходим к закону Ома для однородного участка цепи: Если же электрическая цепь замкнута, то Тогда получаем закон Ома для замкнутой цепи где –э.д.с. действующая в цепи , – суммарное сопротивление всей цепи . В общем случае где - внутренне сопротивление источника тока , –сопротивление внешней цепи. Поэтому закон Ома для замкнутой цепи будет иметь вид Если цепь разомкнута и, следовательно, в ней ток отсутствует то из закона Ома получим, что т.е. э.д.с., действующая в разомкнутой цепи, равна разности потенциалов на ее концах.

48. Разветвленные цепи. Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю: 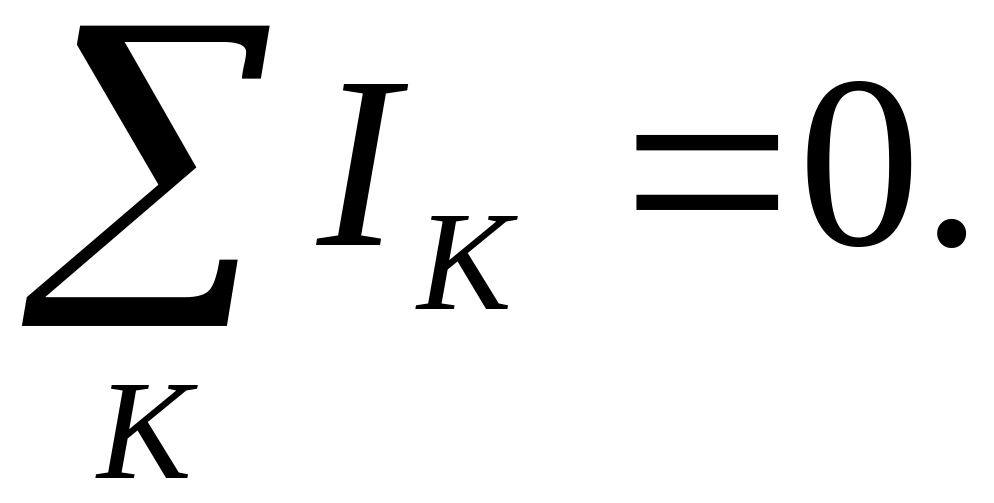Первое правило Кирхгофа вытекает из закона сохранения электрического заряда. Действительно, в случае установившегося постоянного тока ни в одной точке проводника и ни на одном его участке не должны накапливаться электрические заряды. Второе правило Кирхгофа: в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов на сопротивления соответствующих участков этого контура равна алгебраической сумме э.д.с. встречающихся в этом контуре: 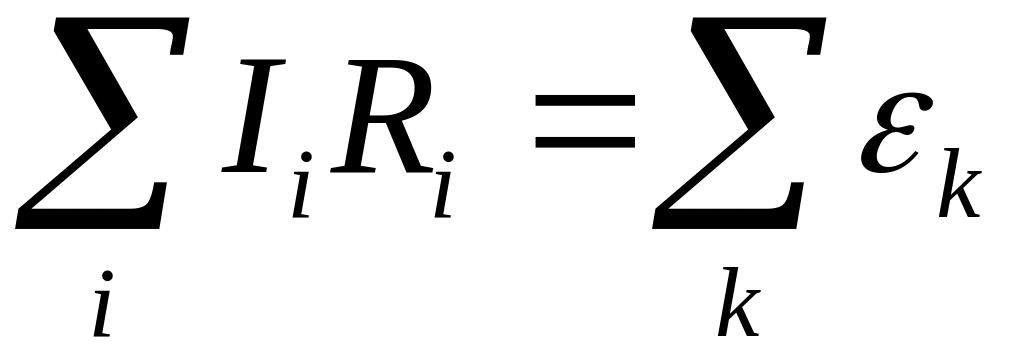. При расчете сложных цепей постоянного тока с применением правил Кирхгофа необходимо: 1) Выбрать произвольное направление токов на всех участках цепи; действительное направление токов определяется при решении задачи: если искомый ток получится положительным, то его направление было выбрано правильно, отрицательным – его истинное направление противоположно выбранному.

2) Выбрать направление обхода контура и строго его придерживаться; произведение положительно, если ток на данном участке совпадает с направлением обхода, и, наоборот, э.д.с., действующие по выбранному направлению обхода, считаются положительными, против – отрицательными.

3) Составить столько уравнений, чтобы их число было равно числу искомых величин; каждый рассматриваемый контур должен содержать хотя бы один элемент, не содержащийся в предыдущих контурах, иначе получается уравнения, являющиеся простой комбинацией уже составленных.