Дифференциальная формулировка потенциальности электростатического поля

Если известно распределение потенциала, т. е. его значение в каждой точке поля, то можно найти напряженность этого поля в каждой точке.

Р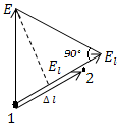 ассмотрим в однородном поле две точки 1 и 2 и предположим, что заряд +1 из точки 1 переходит в точку 2 вдоль отрезка .

(1)

– проекция напряженности Е на направлении .

Введем теперь приращение потенциала при перемещении , т. е. разность потенциалов в точке 2 и точке 1 и будем обозначать его просто , тогда

(2)

(3) (3.а)

Физический смысл выражения следующий: напряженность поля измеряется уменьшение потенциала, приходящееся на единицу длины вдоль линии напряженности.

Связь между напряженностью поля и потенциалом можно выразить с помощью понятия градиента потенциала. Градиентом любой скалярный величины φ в векторном анализе называют вектор, направление которого совпадает с направлением быстрейшего увеличения величины φ. Величина же этого вектора равна изменению φ при перемещении на единицу длины в направлении быстрейшего изменения.

Введем единичный вектор , совпадающий с направлением линии напряженности, тогда векторное значение Е выражается:

,

т. е. напряженность электростатического поля равна градиенту потенциала с обратным знаком:

E = - grad φ

В случае неоднородного поля имеем

Составляющие вектора напряженности по осям прямоугольной системы координат равен:

При этом модуль вектора напряженности:

ед. СГСЕ напр.

Вывод: распределение потенциалов в пространстве однозначно определяет поле вектора . В этом смысле электростатическое поле часто называют потенциальным полем, понимая под этим, что скалярная функция u однозначно определяет векторное поле напряженности. Одним из характерных свойств потенциального поля является равенство нулю циркуляции напряженности этого поля.

Потенциал точечного заряда

Пусть поле точечного заряда q исследуется зарядом Q.

;

Л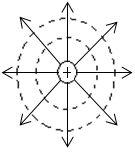 инии напряженности совпадают с радиусами

Интегрируя последнее выражение, найдем:

т.к. потенциал в бесконечности (r= ) равен нулю ( , то С=0

Энергия заряда в поле точечного заряда q равна:

;

Работа перемещения в таком поле равна:

Поле диполя

Система из двух точечных зарядов +q и –q, находящихся на расстоянии друг от друга, называются диполем.

Такую систему в физике рассматривают потому, что центры положительных и отрицательных зарядов молекул многих веществ можно представить с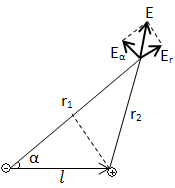 мещенными друг относительно друга. Представление о диполях часто позволяет с известным приближением описать воздействие молекул различных веществ. Модель дипольного состояния вещества лежит в основе диэлектриков.

Произведение положительного заряда на расстояние между зарядами называется моментом диполя:

P=

Если расстояние вектор, направленный от (-) к (+), то .

Рассмотрим жесткие диполи. Согласно принципа суперпозиции

Путь точка наблюдения выбрана так, что длина .

;

α-угол между направлением момента диполя и направлением к точке наблюдения, проведенным из диполя.

Зная зависимость потенциала от координат, можно найти напряженность. Пользуемся полярными координатами r и α.

;

Полная напряженность в точке наблюдения равна:

Если α=0 или α=π, то

Эта формула выражает напряженность поля для точек, лежащих на линии момента диполя.

Если или , то

Эта формула определяет напряженность поля по линии, перпендикулярной к моменту диполя.