Т еорема Остроградского-Гаусса в дифференциальной форме

Теорема Остроградского-Гаусса связывает значение электрического смещения в точках некоторой замкнутой поверхности с величиной заряда, находящегося внутри объема, ограниченного этой поверхностью, т. е. связывает величины, относящиеся к разным точкам поля.

Точка а(x; y; z)→D(D_x; D_y; D_z)

Рассмотрим бесконечно малый параллелепипед с вершиной в точке а и ребрами dx, dy, dz параллельный осям координат.

Поток через грань dy, dz есть -D_x dy dz. Знак минус входит потому, что внешняя нормаль к dy dz и положительное направление D_x составляет <α=π; cos π=-1. Поток через параллельную ей грань, смещенную вдоль Х на dx есть . Поэтому поток через обе ее грани равен

,

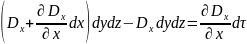– общий поток через всю поверхность параллелепипеда.

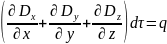
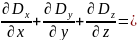
; – уравнение Пуассона

; →

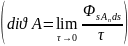
Потенциальный характер электростатического поля. Скалярный потенциал. Потенциал точечного заряда

Электрическое поле неподвижных зарядов называют также электростатическим, параметры этого поля не зависят от времени и являются функциями координат.

Рассмотрим пробный заряд в электростатическом поле. Заряд под действием поля может прийти в действие

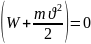
При действии нельзя обнаружить какие-либо изменения в окружающей среде. Работа перемещения заряда в электростатическом поле, изменение кинетической энергии могут иметь место за счет особого вида потенциальной энергии как результата взаимодействия заряда с полем.

Энергия заряда в электростатическом поле зависит от положения заряда и поэтому является потенциальной энергией.

Потенциал поля есть величина, равная отношению потенциальной энергии заряда к величине заряда, помещенного в данную точку электрического поля.

1В = 1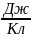

За единицу потенциала в системе СИ принимается потенциал такой точки поля, в которой единица заряда в 1Кл обладает потенциальной энергией в 1Дж.

1В = СГСЕ ед. пот.

Разность потенциалов

И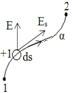 з точки 1 в точке 2 перемещается заряд . Работа, совершаемая зарядом, не зависит от формы пути. Она зависит от соответствующего электростатического поля и может служить его характеристикой. Она называется разностью потенциалов точек 1 и 2 или электростатическим напряжением.

Разность потенциалов двух точек 1 и 2 в электростатическом поле измеряется работой, совершаемой силами поля при перемещении заряда +1 из точки 1 в точку 2.

Зная напряженность в каждой точке, можно вычислить и разность потенциалов любых двух точек.

ds – элемент перемещения заряда.

E_s – проекция вектора напряженности поля на направление ds, то работа при перемещении заряда +1 на отрезок ds есть E_s ds.

Поэтому разность потенциалов .

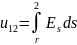А₁₂=qu₁₂, если не единичный заряд.

Физический смысл имеет только разность потенциалов между двумя точками поля, т. к. работа определена тогда, когда заданы две точки – начало и конец пути. Но иногда говорят о потенциале в данной точке.

В электростатическом поле заряд не зависит от формы пути.

U₁₂+U₂₁=U₁₂-U₁₂=0

В электростатическом поле напряжение вдоль замкнутого контура всегда равно нулю. – свойство электростатического поля.

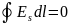
Величина 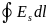подвергающееся циркуляцией вектора напряженности – это есть работа перемещения по замкнутому контуру единичного заряда. С точки зрения силовой характеристики нулевое значение циркуляции объясняется тем, что линии напряженности не могут быть замкнутыми линиями. Поэтому при перемещении заряда по замкнутой линии на одних участках работа электростатических сил >0, на других - <0, результирующая работа равна нулю.

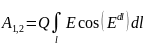
Понятие разности потенциалов широко используют по двум основным причинам:

1. Описание электростатического поля при помощи потенциала гораздо проще, чем при помощи напряженности. Е – вектор, для каждой точки поля нужно знать 3 скалярные величины – составляющие напряженности по координатам. Потенциал – скаляр и вполне определяется величина в каждой точке поля.

2. Разность потенциалов легче измерить, чем напряженность.