2.2 Методы определения лимитирующей стадии гетерогенного процесса.

1. По зависимости общей скорости процесса от скорости обтекания частиц твердого вещества потоком жидкости (сжимаемой – газа, или капельной –несжимаемой).

Если процесс протекает в диффузионной области, то его скорость, как и скорость массопередачи будут зависеть от скорости движения жидкости. Если режим движения жидкости при обтекании является турбулентным, то наблюдаемая скорость процесса будет пропорциональна скорости движения жидкости в степени 0.8. Если режим движения ламинарный, то скорость процесса будет зависеть от скорости потока в степени 0.5.

Т аким образом,

Для турбулентного режима:

Д ля ламинарного режима

скорость процесса при отсутствии обтекания

скорость обтекания твердой частицы жидкостью

2. По температурной зависимости наблюдаемой константы скорости.

Если так называемая эффективная энергия активации гетерогенного процесса составляет величину более 40 кДж/моль, то процесс лимитируется скоростью химической реакции и протекает в кинетической области.

Если эффективная энергия активации равна 10-20 кДж/ моль, то процесс проходит в диффузионной области. Если эффективная энергия активации лежит в пределах от 20 до 40 кДж/моль, то процесс происходит в смешанной, диффузионно-кинетической области.

Если исследовать температурную зависимость наблюдаемой константы скорости гетерогенного процесса в широких температурных пределах, то можно наблюдать переход из кинетической области в диффузионную, вследствие того, что при дальнейшем росте скорости реакции транспорт реагента к поверхности реакции становится меньше скорости его расхода и процесс переходит в диффузионную область.

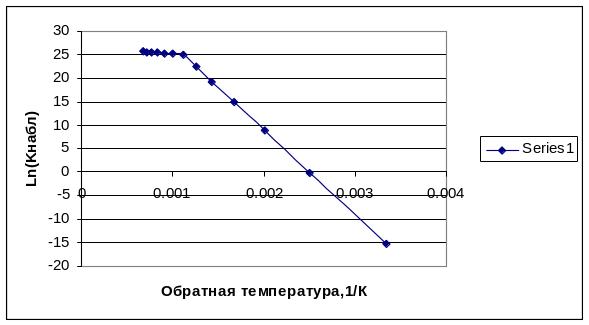
Рис.2.4.Температурная зависимость наблюдаемой константы скорости гетерогенного процесса в координатах уравнения Аррениуса

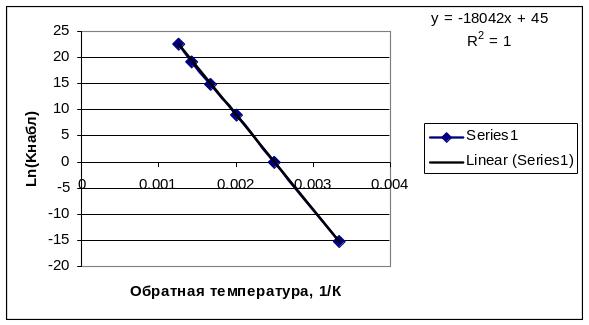
Р ис.2.4а. Температурная зависимость константы скорости в кинетической области

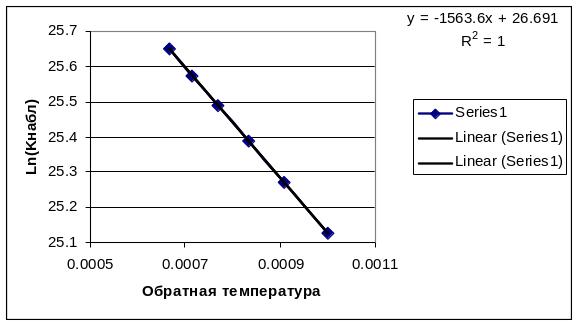
Р ис.2.4б. Температурная зависимость константы скорости в диффузионной области.

Учет внутренней диффузии в гетерогенных каталитических

процессах.

Катализаторы для каталитических процессов изготавливают обычно в виде частиц различной формы чаще всего в виде таблеток цилиндрической или сферической формы. Таблетки обычно имеют развитую пористую структуру, что позволяет создавать катализаторы, имеющие внутреннюю поверхность пор, достигающих нескольких сотен м² на грамм. При такой структуре частиц большая часть химических превращений протекает внутри частицы катализатора. Рассмотрим вывод уравнения математической модели каталитического процесса, протекающего внутри пористой частицы катализатора. Для анализа процессов и вывода уравнений математической модели чаще всего используют так называемую квазигомогенную модель частицы катализатора. В соответствии с этой моделью частицу рассматривают как некую изотропную среду, обладающую проницаемостью для реагентов и продуктов реакции и обладающую каталитическими свойствами к превращению исходного реагента в продукты реакции.

При этих допущениях можно считать, что транспорт вещества внутри пористой частицы катализатора подчинятся закону диффузии Фика, а скорость гетерогенной реакции на внутренней поверхности катализатора может быть отнесена к единице объема катализатора при введении так называемой удельной поверхности, т.е. поверхности, отнесенной к единице объема катализатора.

В этом случае, частица катализатора может характеризоваться эффективным коэффициентом диффузии, D_eff и константой скоростью, отнесенной к единице объема катализатора k_v.

С учетом введенных понятий, можно записать:

Где - коэффициент молекулярной диффузии, м²/с

- пористость частицы, отношение свободного объема пор V_пор к объему

катализатора V_кат, м³/ м³.

- коэффициент извилистости поры, отношение средней длины

транспортной поры к радиусу частицы катализатора , м/м

константа скорости гетерогенного процесса, отнесенная к единице

объема пористой частицы катализатора, 1/сек (для реакции первого

порядка)

k_het - константа скорости гетерогенного процесса, м/сек (для реакции

первого порядка).

S_уд- удельная поверхность катализатора, отнесенная к единице объема

твердой фазы, м²/м³.

Рассмотрим сферическую частицу катализатора, окруженную сплошной средой с концентрацией реагента с_v, кмоль/м³. Концентрацию на поверхности частицы будем считать равной концентрации вдали от поверхности вследствие интенсивного массообмена. На поверхности катализатора происходит реакция 1-го порядка, в результате которой исходное вещество превращается в продукт реакции по схеме:

Рис. 2.5. Схема диффузии реагента

внутри частицы катализатора

В качестве начальных условий обычно задают профиль концентрации по радиусу в начальный момент времени, а в качестве граничных условий задают значения концентраций и ее производных на границах частицы и внутри.

Р ассмотрим решение уравнения (2.19) с граничными условиями (2.21) при стационарном режиме работы катализатора, т.е. при условии, что

Уравнение для стационарных условий будет иметь вид:

(2.22)

Разделим обе части уравнения (2.22) на коэффициент диффузии D и введем новую переменную – безразмерный радиус , где -радиус частицы

У равнение примет вид:

(2.23)

Уравнение (2.23) имеет общее решение в виде:

(2.24)

Где А₁ и А₂ постоянные интегрирования определяемые из граничных условий, учитывающих массобмен на границе и изотропность свойств катализатора.

- модуль Тиле, учитывающий соотношение интенсивности потока внутрь частицы за счет диффузии и расход вещества за счет химической реакции. Это важнейший массообменный параметр, учитывающей доступность внутренней поверхности катализатора для химической реакции.

Доступность внутренней поверхности катализатора для химической реакции принято характеризовать коэффициентом использования внутренней поверхности катализатораю

Коэффициент эффективности использования внутренней поверхности катализатора, или фактор эффективности - отношение количества вещества реагирующего в объеме частицы катализатора с учетом распределения концентрации по радиусу в соответствии с уравнением (2.30) к предельно возможному количеству при отсутствии внутри диффузионного торможения. Это количество будет равно произведению объема частицы на скорость реакции в единице объема при концентрации внутри частицы, равной концентрации в объеме:

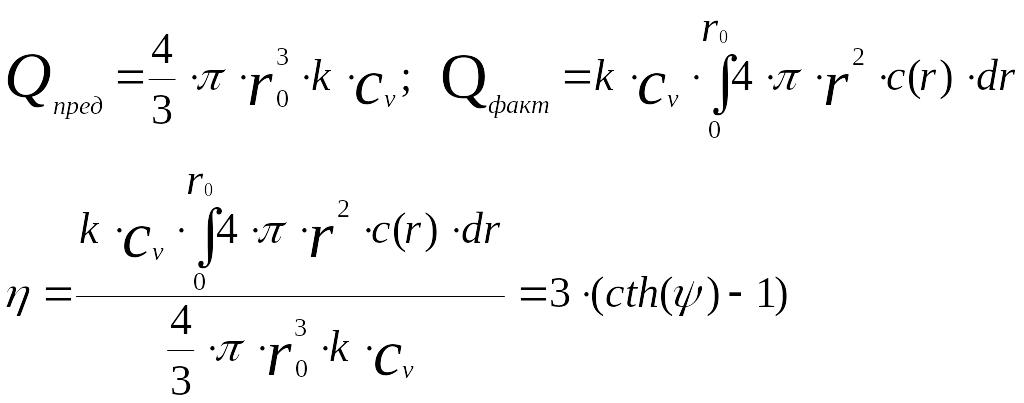
Таким образом, можно определить размер частиц катализатора, обеспечивающий достаточно эффективное использование внутренней поверхности катализатора.

На рисунке показана зависимость фактора эффективности от величины модуля Тиле

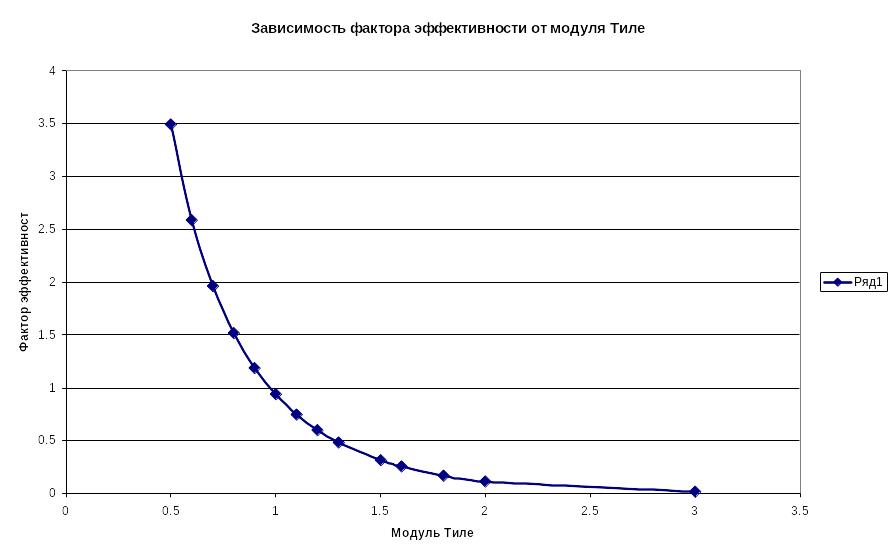
Рисунок.3 Зависимость фактора эффективности от модуля Тиле.

Из рисунка видно, что наиболее приемлемые величины модуля Тиле, обеспечивающие эффективное использование внутренней поверхности катализатора находятся в интервале =0.11.0. Поскольку величина Модуля Тиле состоит из двух сомножителей, то очевидно, что для уменьшения этой величины при постоянной константе скорости, определяемой химической природой реагентов и катализатора, нужно либо уменьшать размер частиц, либо увеличивать коэффициент диффузии реагентов.

Использование квазигомогенной модели для моделирования гетерогенных процессов.